Small-Angle Approximation

The small-angle approximation is the term for the following estimates of the basic trigonometric functions, valid when $\theta \approx 0:$

$$\sin \theta \approx \theta, \qquad \cos \theta \approx 1 - \frac{\theta^2}{2} \approx 1, \qquad \tan \theta \approx \theta.$$

These estimates are widely used throughout mathematics and the physical sciences to simplify equations and make problems analytically tractable. For instance, solving a differential equation that looks like

$$\ddot{\theta} + \sin (\theta) = 0$$

is much trickier than solving its small-angle approximation

$$\ddot{\theta} + \theta= 0,$$

and the solutions to the latter are much more useful than the solutions to the former:

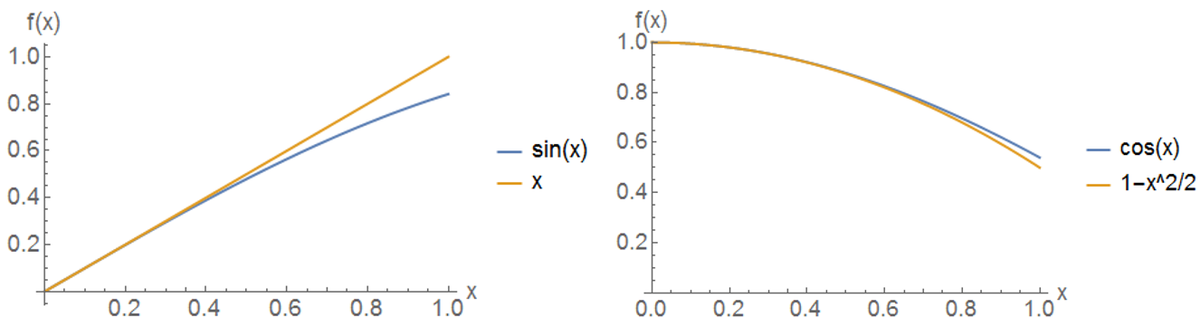Left: $\sin(x)$ and its small-angle approximation near $x=0$. Right: $\cos(x)$ and its small-angle approximation near $x=0$.

Geometrically

The small-angle approximations can be derived geometrically without the use of calculus. Consider the below diagram of a right triangle with one side tangent to a circle:

A right triangle with two sides formed from the radii of a circle and the third side tangent to the circle.

As long as the angle $\theta$ is sufficiently small, the length of $s$ $($the arc subtended by $\theta)$ is very close to that of $s^{\prime}$, the third side of the triangle. The small-angle approximation thus corresponds to $s\approx s^{\prime}$ in this diagram.

From the law of sines,

$$\frac{s^{\prime}}{\sin \theta} = \frac{r}{\sin 90^{\circ}} = r \implies s^{\prime} = r\sin \theta.$$

From the formula for arc length, $s = r \theta$. Comparing the expression for $s$ to the expression for $s^{\prime}$, the small-angle approximation $s\approx s^{\prime}$ must correspond to

$$\sin \theta \approx \theta.$$

Using the double angle identity $\cos 2 x = 1-2\sin^2 x$ with $x = \frac{\theta}{2}$ and substituting in $\sin \theta \approx \theta$, one obtains the small-angle approximation for cosine:

$$\cos \theta = 1 -2\sin^2 \frac{\theta}{2} \approx 1 - 2\left(\frac{\theta}{2}\right)^2 = 1 - \frac{\theta^2}{2} \approx 1.$$

Using Calculus

The most straightforward way of deriving the small-angle approximations uses the calculus technique of Taylor series approximation for both sine and cosine:

$$\begin{aligned} \sin \theta &= \sum_{n=0}^{\infty} \frac{(-1)^n \theta^{2n+1}}{(2n+1)!} = \theta - \frac{\theta^3}{3!} + \mathcal{O} (\theta^5) \\ \cos \theta &= \sum_{n=0}^{\infty} \frac{(-1)^n \theta^{2n}}{(2n)!} = 1 - \frac{\theta^2}{2!} + \mathcal{O} (\theta^4). \end{aligned}$$

The small-angle approximations correspond to the low-order approximations of these Taylor series, as can be seen from the expansions above.

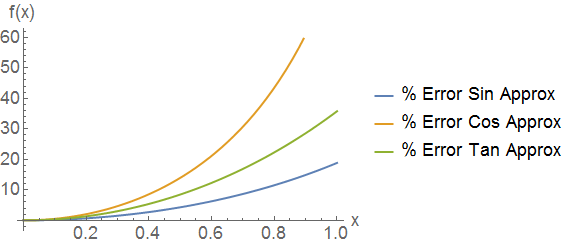Percent errors for each of the small-angle approximations $\sin(x) \approx x$, $\cos (x) \approx 1$, and $\tan (x) \approx x$. For very small angles $(x<0.1),$ the approximation is excellent and the error is very small.

What is the small-angle approximation to $f(x) = \sec x \tan x?$

---

The Taylor series for this function is

$$f(x) = x + \frac{5}{6} x^3 + \frac{61}{120} x^5 + \mathcal{O} \big(x^7\big).$$

The lowest-order small-angle approximation is therefore $f(x) \approx x$. This is consistent with substituting in the small-angle approximations for the sine and cosine functions, which gives

$$\sec x \approx 1, \tan x \approx x \implies \sec x \tan x \approx x.\ _\square$$

Find the small-angle approximation to

$$f(x) = \frac{\sec x \tan x - \csc^2 x}{\cot^2 x}.$$

---

Naively substituting $\sin (x) \approx x$ and $\cos x \approx 1$, one finds the approximation

$$f(x) = \frac{x - \frac{1}{x^2}}{\frac{1}{x^2}} = x^3 - 1.$$

Using the improved approximation for the cosine function, $\cos x \approx 1 - \frac{x^2}{2}$, one obtains

$$f(x) = \frac{\frac{x}{\left(1-\frac{x^2}{2}\right)^2} - \frac{1}{x^2}}{\frac{\left(1-\frac{x^2}{2}\right)^2}{x^2}} = -1-x^2+x^3 -\frac{3}{4} x^4 \mathcal{O} \big(x^5\big).$$

If we instead Taylor expand the given function $f(x)$ directly, we obtain

$$f(x) \approx -1 - x^2 + x^3 - \frac23 x^4 + \mathcal{O} \big(x^5\big),$$

which agrees with the improved approximation to the first three orders.

Plotting the three approximations, we see that the naive approximation does quite poorly, while the improved approximation is much better. The improved approximation for cosine added a lower-order term that was missed by the naive approximation, illustrating the dangers involved in naively approximating when dividing by functions. For the best accuracy, the Taylor series of $f(x)$ itself should be used as opposed to the series for sine and cosine separately:

Small-angle approximations to $f(x)$ based on different truncations of the Taylor series for cosine. The refined truncation is necessary to obtain any useful precision for small angles.

The small-angle approximation is used ubiquitously throughout fields of physics including mechanics, waves and optics, electromagnetism, astronomy, and more. Below, a few well-known examples are explored to illustrate why the small-angle approximation is useful in physics.

The Simple Pendulum

Small oscillations of a simple pendulum are best modeled using the small-angle approximation.

The small oscillations of a simple pendulum are a basic example in mechanics where the small-angle approximation is absolutely essential to making any useful analytic progress. From the rotational form of Newton's second law, the torque $\tau$ on a pendulum of mass $m$ from gravity as it oscillates about a pivot point on a string of length $\ell$ is

$$\tau = I \alpha \implies -\ell mg \sin \theta = m\ell^2 \ddot{\theta} \implies \ddot{\theta} + \frac{g}{\ell} \sin \theta = 0,$$

where $\theta$ is the angle between the string and the vertical.

The solutions to this equation of motion can be found in terms of functions called elliptic integrals, which are difficult to work with by hand. However, employing the small-angle approximation,

$$\ddot{\theta} + \frac{g}{\ell} \sin \theta = 0 \implies \ddot{\theta} + \frac{g}{\ell} \theta = 0.$$

The new differential equation is easily solvable. The solutions go as $\theta(t) = A\cos \left(\sqrt{\frac{g}{\ell}} t\right)+B\sin\left(\sqrt{\frac{g}{\ell}} t\right)$ for constants $A$ and $B$ depending on initial conditions, successfully reproducing the oscillatory behavior of the pendulum.

Angular Distance in Astronomy

The size or distance between celestial bodies in astronomy is typically written in terms of the angular diameter or apparent size, i.e. the angle $\theta$ between the two bodies as seen from Earth. If the separation between two faraway points is $d$ and the midpoint between the points is at distance $D$ from Earth, then this angle obeys the relationship

$$\tan \frac{\theta}{2} = \frac{d}{2D}.$$

The diagram corresponding to this formula is below:

Angular separation between two faraway stars as seen from Earth

Using the small-angle approximation, the angular distance can be rewritten as

$$\theta = \frac{d}{D}.$$

The approximation is useful because typically the angular distance is the easiest to measure in astronomy and the difference between angles is so small that the angle itself is more useful than the sine.

There are 60 arcminutes in a degree, and the sun has an angular diameter of approximately $32$ arcminutes. Knowing that the sun is about $8$ light-minutes away from Earth, estimate the diameter of the sun.

---

First, convert $8$ light-minutes into the earth-sun distance $D:$

$$D = ct = (3 \times 10^{8} \text{ m}/\text{s})(8\times 60 \text{ s}) = 1.44 \times 10^{11} \text{ m}.$$

Using the formula for angular distance in the small-angle approximation,

$$d \approx \theta D = (32 \text{ arcmin})\left(\frac{1^{\circ}}{60 \text{ arcmin}}\right) \left(\frac{2\pi \text{ radians}}{360^{\circ}}\right) \left(1.44 \times 10^{11} \text{ m}\right) = 1.34 \times 10^9 \text{ m},$$

which is accurate to less than $5 \%$ error. $_\square$

Single-Slit Diffraction

In single-slit diffraction, light passing through a barrier with a slit larger than one wavelength of the light has an intensity profile measured behind the barrier which exhibits a characteristic pattern of peaks and troughs. The condition for a minimum in this intensity distribution is

$$d \sin \theta = m \lambda,$$

where $d$ is the slit width, $\theta$ is the angle to the point of measurement from the center of the slit, $\lambda$ is the wavelength of the light, and $m$ is a nonzero integer.

This condition can be rewritten in terms of the vertical distance from the center of the measurement screen, $y$, as shown in the above diagram. Suppose the measurement screen is a distance of $D$ from the barrier. Typically, $D$ is taken to be much greater than $d$, and the small-angle approximation for $\theta$ can be used. Then the formula for intensity minima becomes

$$y = \frac{m \lambda D}{d},$$

a convenient expression in terms of the wavelength of the light, width of the slit, and distance from the barrier to the screen.