Supervised Learning
Supervised learning is the machine learning task of determining a function from labeled data. For example, in a machine learning algorithm that detects if a post is spam or not, the training set would include posts labeled as "spam" and posts labeled as "not spam" to help teach the algorithm how to recognize the difference. Supervised learning algorithms infer a function from labeled data and use this function on new examples. Supervised learning is a core concept of machine learning and is used in areas such as bioinformatics, computer vision, and pattern recognition.
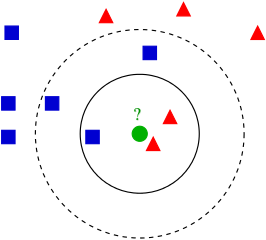 An example of k-nearest neighbors, a supervised learning algorithm. The algorithm determines the classification of a data point by looking at its k nearest neighbors.[1]
An example of k-nearest neighbors, a supervised learning algorithm. The algorithm determines the classification of a data point by looking at its k nearest neighbors.[1]
Contents
Overview
Supervised learning begins by operating on a training dataset, data points that are labeled with their appropriate outputs. For example, in the image above, the training set would be the location of the blue squares and the red triangles, and the labels for each data point would be whether the point is a blue square or a red triangle. The learning algorithm looks for a function \(g(x)\) that can map the input data \(x\) to their appropriate labels \(y\) well. The overall goal of the algorithm is to generalize this function so that it performs well on unknown examples.
The most widely used supervised learning algorithms are:
Risks
In determining how good a specific supervised learning algorithm is, two types of risks can be minimized:
- Empirical risk - Empirical risk is the expected loss of the function \(g\) that the supervised learning algorithm infers from the training dataset. For example, if \(g\) correctly maps all training data points \(x_i\) to their respective labels \(y_i\), the empirical risk is 0. Mathematically, the empirical risk function for \(N\) training data points is \(R(g) = \frac{1}{N}\sum\limits_{i=1}^{N} L(y_i, g(x_i))\), where \(L\) is the user-defined loss function that determines the penalty of incorrectly labeling a specific data point.
In minimizing empirical risk, the supervised learning algorithm is taught to match the training data as well as possible. However, as shown in the image below, a solution can minimize empirical risk without being a good candidate function for unknown data points. This is called overfitting, which occurs when the proposed function focuses more on noise rather than the actual data, as seen below with the blue line.
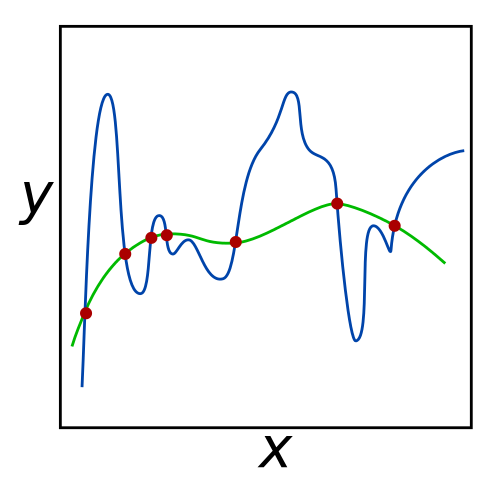 For the given set of red input points, both the green and blue lines minimize error to 0. However, the green line may be more successful at predicting the coordinates of unknown data points, since it seems to generalize the data better.[2]
For the given set of red input points, both the green and blue lines minimize error to 0. However, the green line may be more successful at predicting the coordinates of unknown data points, since it seems to generalize the data better.[2]
- Structural risk - Structural risk is used to prevent the supervised learning algorithm from overfitting the training data. Structural risk minimization introduces a regularization penalty that can prefer certain solutions over others. Mathematically, the regularization penalty is a function \(C(g)\) that is used along with empirical risk to determine a solution. Specifically, structural risk minimizes \(R(g) + \lambda C(g)\), where \(R(g)\) is empirical risk and \(\lambda\) is a user-defined parameter that controls the regularization penalty. For example, if \(\lambda=0\), the optimization problem minimizes empirical risk as before.
A good way of determining an appropriate value for \(\lambda\) is by using cross validation, a method that trains the supervised algorithm on training data and tests its performance on a validation dataset (data points where the correct label is known). The algorithm is then updated to minimize its error on the validation set, while still being trained on the training dataset. An example of this in action is described in ridge regression, and is widely used to determine functions that perform well on unknown data.
Challenges
There are many challenges in constructing supervised learning algorithms, with four important ones described below.
- Bias-variance tradeoff - Suppose a supervised learning algorithm is trained on multiple datasets. If the algorithm is unable to correctly label a specific data point, it is said to be biased for that input. Additionally, if the algorithm produces different output values when trained on different datasets, it is said to have high variance. Empirical risk focuses on bias, whereas structural risk focuses on variance. There is usually a tradeoff between bias and variance, where a low bias implies high variance and vice-versa. A problem for supervised algorithms is finding the balance between these two concepts that works best with unknown data points.
 The blue curve minimizes the error of the data points (low bias) but has high variance. Conversely, the black line does not minimize errors (has a higher bias), but fits the data well (low variance).[3]
The blue curve minimizes the error of the data points (low bias) but has high variance. Conversely, the black line does not minimize errors (has a higher bias), but fits the data well (low variance).[3] Complexity - The function that the supervised learning algorithm is trying to mimic could be either simple or complex. If the expected function is simple, the algorithm should have low variance to well fit the data. However, if the expected function is complex, the algorithm should have high variance to adapt to unknown data points. Supervised learning algorithms should be able to determine variance appropriately based on the amount of data and the type of function to be expecting.
Many dimensions - When a supervised learning algorithm is given a dataset consisting of many dimensions, it may attempt to identify trends between irrelevant factors. This increases the variance of the inferred function and can decrease the accuracy of the algorithm. Two ways of combating this issue include running a different algorithm to discard irrelevant variables and reducing the input data to a lower number of dimensions.
Format of Data - If the training data has errors in its labeling or in its data value, the supervised learning algorithm should not attempt to exactly match the training examples. This can lead to overfitting and will not perform well for unknown values. Additionally, if the training data contains redundant information, supervised learning algorithms may perform poorly due to over-relying on specific examples. Filtering the data or regularizing the algorithm properly can mitigate these two issues.
References
- Ajanki, A. Example of k-nearest neighbour classificationnb. Retrieved May 28, 2016, from https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm#/media/File:KnnClassification.svg
- Nicoguaro, . Regularization.svg. Retrieved May 31, 2016, from https://en.wikipedia.org/wiki/File:Regularization.svg
- Ghiles, . Overfitted_Data.svg. Retrieved May 31, 2016, from https://en.wikipedia.org/wiki/File:Overfitted_Data.png