Artificial Neural Network
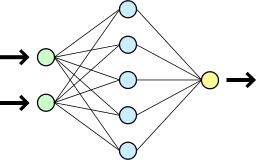 A simple artificial neural network. The first column of circles represents the ANN's inputs, the middle column represents computational units that act on that input, and the third column represents the ANN's output. Lines connecting circles indicate dependencies.[1]
A simple artificial neural network. The first column of circles represents the ANN's inputs, the middle column represents computational units that act on that input, and the third column represents the ANN's output. Lines connecting circles indicate dependencies.[1]
Artificial neural networks (ANNs) are computational models inspired by the human brain. They are comprised of a large number of connected nodes, each of which performs a simple mathematical operation. Each node's output is determined by this operation, as well as a set of parameters that are specific to that node. By connecting these nodes together and carefully setting their parameters, very complex functions can be learned and calculated.
Artificial neural networks are responsible for many of the recent advances in artificial intelligence, including voice recognition, image recognition, and robotics. For example, ANNs can perform image recognition on hand drawn digits. An interactive example can be found here.
Contents
Online Learning
With the advent of computers in the 1940s, computer scientists' attention turned towards developing intelligent systems that could learn to perform prediction and decision making. Of particular interest were algorithms that could perform online learning, which is a learning method that can be applied to data points arriving sequentially. This is in opposition to batch learning, which requires that all of the data be present at the time of training.
Online learning is especially useful in scenarios where training data is arriving sequentially over time, such as speech data or the movement of stock prices. With a system capable of online learning, one doesn't have to wait until the system has received a ton of data before it can make a prediction or decision. If the human brain learned by batch learning, then human children would take 10 years before they could learn to speak, mostly just to gather enough speech data and grammatical rules to speak correctly. Instead, children learn to speak by observing the speech patterns of those around them and gradually incorporating that knowledge to improve their own speech, an example of online learning.
Given that the brain is such a powerful online learner, it is natural to try to emulate it mathematically. ANNs are one attempt at a model with the bare minimum level of complexity required to approximate the function of the human brain, and so are among the most powerful machine learning methods discovered thus far.
Neurons
The human brain is primarily comprised of neurons, small cells that learn to fire electrical and chemical signals based on some function. There are on the order of \(10^{11}\) neurons in the human brain, about \(15\) times the total number of people in the world. Each neuron is, on average, connected to \(10000\) other neurons, so that there are a total of \(10^{15}\) connections between neurons.
 Neurons and microglial cells stained red and green respectively.[2]
Neurons and microglial cells stained red and green respectively.[2]
Since individual neurons aren't capable of very complicated calculations, it is thought that the huge number of neurons and connections are what gives the brain its computational power. While there are in fact thousands of different types of neurons in the human brain, ANNs usually attempt to replicate only one type in an effort to simplify the model calculation and analysis.

Neurons function by firing when they receive enough input from the other neurons to which they're connected. Typically, the output function is modeled as an activation function, where inputs below a certain threshold don't cause the neuron to fire, and those above the threshold do. Thus, a neuron exhibits what is known as all-or-nothing firing, meaning it is either firing, or it is completely off and no output is produced.
From the point of view of a particular neuron, its connections can generally be split into two classes, incoming connections and outgoing connections. Incoming connections form the input to the neuron, while the output of the neuron flows through the outgoing connections. Thus, neurons whose incoming connections are the outgoing connections of other neurons treat other neurons' outputs as inputs. The repeated transformation of outputs of some neurons into inputs of other neurons gives rise to the power of the human brain, since the composition of activation functions can create highly complex functions.
It turns out that incoming connections for a particular neuron are not considered equal. Specifically, some incoming connections are stronger than others, and provide more input to a neuron than weak connections. Since a neuron fires when it receives input above a certain threshold, these strong incoming connections contribute more to neural firing. Neurons actually learn to make some connections stronger than others, in a process called long-term potentiation, allowing them to learn when to fire in response to the activities of neurons they're connected to. Neurons can also make connections weaker through an analogous process called long-term depression.
Model Desiderata
As discussed in the above sections, as well as the later section titled The Universal Approximation Theorem, a good computational model of the brain will have three characteristics:
Biologically-Inspired The brain's computational power is derived from its neurons and the connections between them. Thus, a good computational approximation of the brain will have individual computational units (a la neurons), as well as ways for those neurons to communicate (a la connections). Specifically, the outputs of some computational units will be the inputs to other computational units. Furthermore, each computational unit should calculate some function akin to the activation function of real neurons.
Flexible The brain is flexible enough to learn seemingly endless types and forms of data. For example, even though most teenagers under the age of 16 have never driven a car before, most learn very quickly to drive upon receiving their driver's license. No person's brain is preprogrammed to learn how to drive, and yet almost anyone can do it given a small amount of training. The brain's ability to learn to solve new tasks that it has no prior experience with is part of what makes it so powerful. Thus, a good computational approximation of the brain should be able to learn many different types of functions without knowing the forms those functions will take beforehand.
Capable of Online Learning The brain doesn't need to learn everything at once, so neither should a good model of it. Thus, a good computational approximation of the brain should be able to improve by online learning, meaning it gradually improves over time as it learns to correct past errors.
By the first desideratum, the model will consist of many computational units connected in some way. Each computational unit will perform a simple computation whose output will be passed as input to other units. This process will repeat itself some number of times, so that outputs from some computational units are the inputs to others. With any luck, connecting enough of these units together will give sufficient complexity to compute any function, satisfying the second desideratum. However, what kind of function the model ends up computing will depend on the data it is exposed to, as well as a learning algorithm that determines how the model learns that data. Ideally, this algorithm will be able to perform online learning, the third desideratum.
Thus, building a good computational approximation to the brain consists of three steps. The first is to develop a computational model of the neuron and to connect those models together to replicate the way the brain performs computations. This is covered in the sections titled A Computational Model of the Neuron, The Sigmoid Function, and Putting It All Together. The second is to prove that this model is sufficiently complex to calculate any function and learn any type of data it is given, which is covered in the section titled The Universal Approximation Theorem. The third is to develop a learning algorithm that can learn to calculate a function, given a model and some data, in an online manner. This is covered in the section titled Training The Model.
A Computational Model of the Neuron
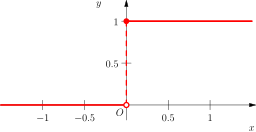 The step function.[4]
The step function.[4]
As stated above, neurons fire above a certain threshold and do nothing below that threshold, so a model of the neuron requires a function exhibiting the same properties. The simplest function that does this is the step function.
The step function is defined as:
\(H(x) = \begin{cases} 1 & \mbox{if } x \ge 0, \\ 0 & \mbox{if } x \lt 0. \\ \end{cases}\)
In this simple neuron model, the input is a single number that must exceed the activation threshold in order to trigger firing. However, neurons can (and should, if they're to do anything useful) have connections to multiple incoming neurons, so we need some way of "integrating" these incoming neuron's inputs into a single number. The most common way of doing this is to take a weighted sum of the neuron's incoming inputs, so that the neuron fires when the weighted sum exceeds the threshold. If the vector of outputs from the incoming neurons is represented by \(\vec{x}\), then the weighted sum of \(\vec{x}\) is the dot product \(\vec{w} \cdot \vec{x}\), where \(\vec{w}\) is called the weight vector.
To further improve the modeling capacity of the neuron, we want to be able to set the threshold arbitrarily. This can be achieved by adding a scalar (which may be positive or negative) to the weighted sum of the inputs. Adding a scalar of \(-b\) will force the neuron's activation threshold to be set to \(b\), since the new step function \(H(x+(-b))\) at \(x = b\) equals \(0\), which is the threshold of the step function. The value \(b\) is known as the bias since it biases the step function away from the natural threshold at \(x = 0\).
Thus, calculating the output of our neuron model is comprised of two steps:
1) Calculate the integration. The integration, as defined above, is the sum \(\vec{w} \cdot \vec{x} + b\) for vectors \(\vec{w}\), \(\vec{x}\) and scalar \(b\).2) Calculate the output. The output is the activation function applied to the result of step 1. Since the activation function in our model is the step function, the output of the neuron is \(H(\vec{w} \cdot \vec{x} + b)\), which is \(1\) when \(\vec{w} \cdot \vec{x} + b >= 0\) and \(0\) otherwise.
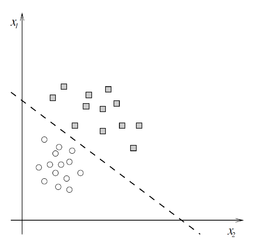 A linear classifier, where squares evaluate to 1 and circles to 0.[5]
A linear classifier, where squares evaluate to 1 and circles to 0.[5]
Following from the description of step 2, our neuron model defines a linear classfier, i.e. a function that splits the inputs into two regions with a linear boundary. In two dimensions, this is a line, while in higher dimensions the boundary is known as a hyperplane. The weight vector \(\vec{w}\) defines the slope of the linear boundary while the bias \(b\) defines the intercept of the linear boundary. The following diagram illustrates a neuron's output for two incoming connections (i.e. a two dimensional input vector \(\vec{x}\). Note that the neuron inputs are clearly separated into values of \(0\) and \(1\) by a line (defined by \(\vec{w} \cdot \vec{x} + b = 0\)).
By adjusting the values of \(\vec{w}\) and \(b\), the step function unit can adjust its linear boundary and learn to split its inputs into classes, \(0\) and \(1\), as shown in the previous image. As a corollary, different values of \(\vec{w}\) and \(b\) for multiple step function units will yield multiple different linear classifiers. Part of what makes ANNs so powerful is their ability to adjust \(\vec{w}\) and \(b\) for many units at the same time, effectively learning many linear classifiers simultaneously. This learning is discussed in more depth in the section titled Training the Model.
The Universal Approximation Theorem
Since the brain can calculate more than just linear functions by connecting many neurons together, this suggests that connecting many linear classifiers together should produce a nonlinear function. In fact, it is proven that for certain activation functions and a very large number of neurons, ANNs can model any continuous, smooth function arbitrarily well, a result known as the universal approximation theorem.
This is very convenient because, like the brain, an ANN should ideally be able to learn any function handed to it. If ANNs could only learn one type of function (e.g. third degree polynomials), this would severely limit the types of problems to which they could be applied. Furthermore, learning often happens in an environment where the type of function to be learned is not known beforehand, so it is advantageous to have a model that does not depend on knowing a priori the form of the data it will be exposed to.
Unfortunately, since the step function can only output two different values, \(0\) and \(1\), an ANN of step function neurons cannot be a universal approximator (generally speaking, continuous functions take on more than two values). Luckily, there is a continuous function called the sigmoid function, described in the next section, that is very similar to the step function and can be used in universal approximators.
The Sigmoid Function
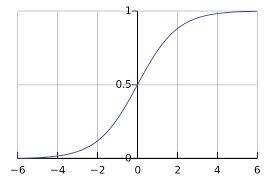 The sigmoid function.[6]
The sigmoid function.[6]
There is a continuous approximation of the step function called the logistic curve, or sigmoid function, denoted as \(\sigma(x)\). This function's output ranges over all values between \(0\) and \(1\) and makes a transition from values near \(0\) to values near \(1\) at \(x = 0\), similar to the step function \(H(x)\).
The sigmoid function is defined as:
\(\sigma(x) = \frac{1}{1 + e^{-x}}\)
So, for a computational unit that uses the sigmoid function, instead of firing \(0\) or \(1\) like a step function unit, it's output will be between \(0\) and \(1\), non-inclusive. This changes slightly the interpretation of this unit as a model of a neuron, since it no longer exhibits all-or-nothing behavior since it will never take on the value of \(0\) (nothing) or \(1\) (all). However, the sigmoid function is very close to \(0\) for \(x \lt 0\) and very close to \(1\) for \(x \gt 0\), so it can be interpreted as exhibiting practically all-or-nothing behavior on most (\(x \not\approx 0\)) inputs.
The output for a sigmoidal unit with weight vector \(\vec{w}\) and bias \(b\) on input \(\vec{x}\) is:
\(\sigma(\vec{w} \cdot \vec{x} + b) = \left(1+\exp\left(-(\vec{w} \cdot \vec{x} + b)\right)\right)^{-1}\)
Thus, a sigmoid unit is like a linear classifier with a boundary defined at \(\vec{w} \cdot \vec{x} + b = 0\). The value of the sigmoid function at the boundary is \(\sigma(0) = .5\). Inputs \(\vec{x}\) that are far from the linear boundary will be approximately \(0\) or \(1\), while those very close to the boundary will be closer to \(.5\).
The sigmoid function turns out to be a member of the class of activation functions for universal approximators, so it imitates the behavior of real neurons (by approximating the step function) while also permitting the possibility of arbitrary function approximation. These happen to be exactly the first two desiderata specified for a good mathematical model of the brain. In fact, some ANNs use activation functions that are different from the sigmoidal function, because those functions are also proven to be in the class of functions for which universal approximators can be built. Two well-known activation functions used in the same manner as the sigmoidal function are the hyperbolic tangent and the rectifier. The proof that these functions can be used to build ANN universal approximators is fairly advanced, so it is not covered here.
Calculate the output of a sigmoidal neuron with weight vector \(\vec{w} = (.25, .75)\) and bias \(b = -.75\) for the following two inputs vectors:
\(\vec{m} = (1, 2)\)
\(\vec{n} = (1, -.5)\)
Recalling that the output of a sigmoidal neuron with input \(\vec{x}\) is \(\sigma(\vec{w} \cdot \vec{x} + b)\),
\(\begin{align*} d &= \vec{w} \cdot \vec{m} + b \\ &= w_1 \cdot m_1 + w_2 \cdot m_2 + b \\ &= .25 \cdot 1 + .75 \cdot 2 -.75 \\ &= 1 \end{align*}\)
\(\begin{align*} s &= \sigma(d) \\ &= \frac{1}{1 + e^{-d}} \\ &= \frac{1}{1+e^{-1}} \\ &= .73105857863 \end{align*}\)
Thus, the output on \(\vec{m} = (1, 2)\) is \(.73105857863\). The same reasoning applied to \(\vec{n} = (1, -.5)\) yields \(.29421497216\).
Like the step function unit describe above, the sigmoid function unit's linear boundary can be adjusted by changing the values of \(\vec{w}\) and \(b\). The weight vector defines the slope of the linear boundary while the bias defines the intercept of the linear boundary. Since, like the brain, the final model will include many individual computational units (a la neurons), a learning algorithm that can learn, or train, many \(\vec{w}\) and \(b\) values simultaneously is required. This algorithm is described in the section titled Training the Model.
Putting It All Together
Neurons are connected to one another, with each neuron's incoming connections made up of the outgoing connections of other neurons. Thus, the ANN will need to connect the outputs of sigmoidal units to the inputs of other sigmoidal units.
One Sigmoidal Unit
The diagram below shows a sigmoidal unit with three inputs \(\vec{x} = (x_1, x_2, x_3)\), one output \(y\), bias \(b\), and weight vector \(\vec{w} = (w_1, w_2, w_3)\). Each of the inputs \(\vec{x} = (x_1, x_2, x_3)\) can be the output of another sigmoidal unit (though it could also be raw input, analogous to unprocessed sense data in the brain, such as sound), and the unit's output \(y\) can be the input to other sigmoidal units (though it could also be a final output, analogous to an action associated neuron in the brain, such as one that bends your left elbow). Notice that each component \(w_i\) of the weight vector corresponds to each component \(x_i\) of the input vector. Thus, the summation of the product of the individual \(w_i, x_i\) pairs is equivalent to the dot product, as discussed in the previous sections.
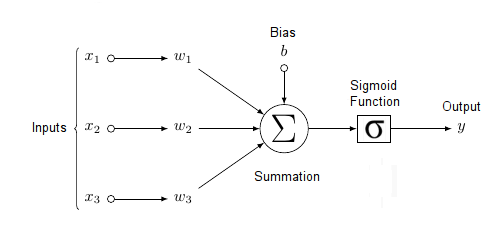 A sigmoidal unit with three inputs \(\vec{x} = (x_1, x_2, x_3)\), weight vector \(\vec{w}\), and bias \(b\).[7]
A sigmoidal unit with three inputs \(\vec{x} = (x_1, x_2, x_3)\), weight vector \(\vec{w}\), and bias \(b\).[7]
ANNs as Graphs
Artificial neural networks are most easily visualized in terms of a directed graph. In the case of sigmoidal units, node \(s\) represents sigmoidal unit \(s\) (as in the diagram above) and directed edge \(e = (u, v)\) indicates that one of sigmoidal unit \(v\)'s inputs is the output of sigmoidal unit \(u\).
Thus, if the diagram above represents sigmoidal unit \(s\) and inputs \(x_1\), \(x_2\), and \(x_3\) are the outputs of sigmoidal units \(a\), \(b\), and \(c\), respectively, then a graph representation of the above sigmoidal unit will have nodes \(a\), \(b\), \(c\), and \(s\) with directed edges \((a, s)\), \((b, s)\), and \((c, s)\). Furthermore, since each incoming directed edge is associated with a component of the weight vector for sigmoidal unit \(s\), each incoming edge will be labeled with its corresponding weight component. Thus edge \((a, s)\) will have label \(w_1\), \((b, s)\) will have label \(w_2\), and \((c, s)\) will have label \(w_3\). The corresponding graph is shown below, with the edges feeding into nodes \(a\), \(b\), and \(c\) representing inputs to those nodes.
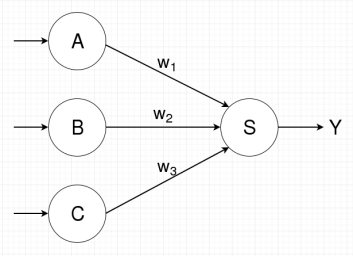 Directed graph representing ANN with sigmoidal units \(a\), \(b\), \(c\), and \(s\). Unit \(s\)'s weight vector \(\vec{w}\) is \((w_1, w_2, w_3)\)
Directed graph representing ANN with sigmoidal units \(a\), \(b\), \(c\), and \(s\). Unit \(s\)'s weight vector \(\vec{w}\) is \((w_1, w_2, w_3)\)
While the above ANN is very simple, ANNs in general can have many more nodes (e.g. modern machine vision applications use ANNs with more than \(10^6\) nodes) in very complicated connection patterns (see the wiki about convolutional neural networks).
The outputs of sigmoidal units are the inputs of other sigmoidal units, indicated by directed edges, so computation follow the edges in the graph representation of the ANN. Thus, in the example above, computation of \(s\)'s output is preceded by the computation of \(a\), \(b\), and \(c\)'s outputs. If the graph above was modified so that's \(s\)'s output was an input of \(a\), a directed edge passing from \(s\) to \(a\) would be added, creating what is known as a cycle. This would mean that \(s\)'s output is dependent on itself. Cyclic computation graphs greatly complicate computation and learning, so computation graphs are commonly restricted to be directed acyclic graphs (or DAGs), which have no cycles. ANNs with DAG computation graphs are known as feedforward neural networks, while ANNs with cycles are known as recurrent neural networks.
Ultimately, ANNs are used to compute and learn functions. This consists of giving the ANN a series of input-output pairs \(\vec{(x_i}, \vec{y_i})\), and training the model to approximate the function \(f\) such that \(f(\vec{x_i}) = \vec{y_i}\) for all pairs. Thus, if \(\vec{x}\) is \(n\)-dimensional and \(\vec{y}\) is \(m\)-dimensional, the final sigmoidal ANN graph will consist of \(n\) input nodes (i.e. raw input, not coming from other sigmoidal units) representing \(\vec{x} = (x_1, \dots, x_n)\), \(k\) sigmoidal units (some of which will be connected to the input nodes), and \(m\) output nodes (i.e. final output, not fed into other sigmoidal units) representing \(\vec{y} = (y_1, \dots, y_m)\).
Like sigmoidal units, output nodes have multiple incoming connections and output one value. This necessitates an integration scheme and an activation function, as defined in the section titled The Step Function. Sometimes, output nodes use the same integration and activation as sigmoidal units, while other times they may use more complicated functions, such as the softmax function, which is heavily used in classification problems. Often, the choice of integration and activation functions is dependent on the form of the output. For example, since sigmoidal units can only output values in the range \((0, 1)\), they are ill-suited to problems where the expected value of \(y\) lies outside that range.
An example graph for an ANN computing a two dimensional output \(\vec{y}\) on a three dimensional input \(\vec{x}\) using five sigmoidal units \(s_1, \dots, s_5\) is shown below. An edge labeled with weight \(w_{ab}\) represents the component of the weight vector for node \(b\) that corresponds to the input coming from node \(a\). Note that this graph, because it has no cycles, is a feedforward neural network.
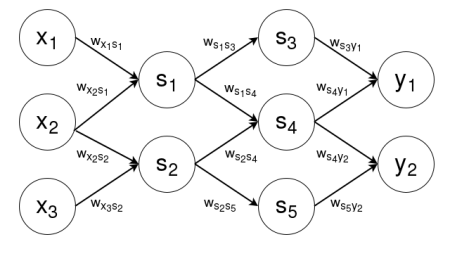 ANN for three dimensional input, two dimensional output, and five sigmoidal units
ANN for three dimensional input, two dimensional output, and five sigmoidal units
Layers
Thus, the above ANN would start by computing the outputs of nodes \(s_1\) and \(s_2\) given \(x_1\), \(x_2\), and \(x_3\). Once that was complete, the ANN would next compute the outputs of nodes \(s_3\), \(s_4\), and \(s_5\), dependent on the outputs of \(s_1\) and \(s_2\). Once that was complete, the ANN would do the final calculation of nodes \(y_1\) and \(y_2\), dependent on the outputs of nodes \(s_3\), \(s_4\), and \(s_5\).
It is obvious from this computational flow that certain sets of nodes tend to be computed at the same time, since a different set of nodes uses their outputs as inputs. For example, set \(\{s_3, s_4, s_5\}\) depends on set \(\{s_1, s_2\}\). These sets of nodes that are computed together are known as layers, and ANNs are generally thought of a series of such layers, with each layer \(l_i\) dependent on previous layer \(l_{i-1}\) Thus, the above graph is composed of four layers. The first layer \(l_0\) is called the input layer (which does not need to be computed, since it is given), while the final layer \(l_3\) is called the output layer. The intermediate layers are known as hidden layers, which in this case are the layers \(l_1 = \{s_1, s_2\}\) and \(l_2 = \{s_3, s_4, s_5\}\), are usually numbered so that hidden layer \(h_i\) corresponds to layer \(l_i\). Thus, hidden layer \(h_1=\{s_1, s_2\}\) and hidden layer \(h_2=\{s_3, s_4, s_5\}\). The diagram below shows the example ANN with each node grouped into its appropriate layer.
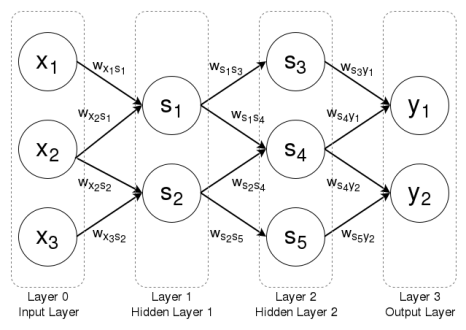 The same ANN grouped into layers
The same ANN grouped into layers
 ANN Layers
The image source: Artificial Neural Network
ANN Layers
The image source: Artificial Neural Network
Training The Model
The ANN can now calculate some function \(f_{\theta}(\vec{x})\) that depends on the values of the individual nodes' weight vectors and biases, which together are known as the ANN's parameters \(\theta\). The logical next step is to determine how to alter those biases and weight vectors so that the ANN computes known values of the function. That is, given a series of input-output pairs \((\vec{x_i}, \vec{y_i})\), how can the weight vectors and biases be altered such that \(f_{\theta}(\vec{x_i}) \approx \vec{y_i}\) for all \(i\)?
Choosing an Error Function
The typical way to do this is define an error function \(E\) over the set of pairs \(X = \{(\vec{x_1}, \vec{y_1}), \dots, (\vec{x_N},\vec{y_N})\}\) such that \(E(X, \theta)\) is small when \(f_{\theta}(\vec{x_i}) \approx \vec{y_i}\) for all \(i\). Common choices for \(E\) are the mean squared error (MSE) in the case of regression problems and the cross entropy in the case of classification problems. Thus, training the ANN reduces to minimizing the error \(E(X, \theta)\) with respect to the parameters (since \(X\) is fixed). For example, for the mean square error function, given two input-output pairs \(X= \{(\vec{x_1}, \vec{y_1}), (\vec{x_2}, \vec{y_2})\}\) and an ANN with parameters \(\theta\) that outputs \( f_{\theta}(\vec{x})\) for input \(\vec{x}\), the error function \(E(X, \theta)\) is
\[E(X, \theta)=\frac{(y_1 - f_{\theta}(\vec{x_1}))^2}{2} + \frac{(y_2 - f_{\theta}(\vec{x_2}))^2}{2}\]
Gradient Descent
Since the error function \(E(X, \theta)\) defines a fairly complex function (it is a function of the output of the ANN, which is a composition of many nonlinear functions), finding the minimum analytically is generally impossible. Luckily, there exists a general method for minimizing differentiable functions called gradient descent. Basically, gradient descent finds the gradient of a function \(f\) at a particular value \(x\) (for an ANN, that value will be the parameters \(\theta\)) and then updates that value by moving (or stepping) in the direction of the negative of the gradient. Generally speaking (it depends on the size of the step \(\eta\)), this will find a nearby value \(x^{\prime} = x - \eta \nabla f(x)\) for which \(f(x^{\prime}) \lt f(x)\). This process repeats until a local minimum is found, or the gradient sufficiently converges (i.e. becomes smaller than some threshold). Learning for an ANN typically starts with a random initialization of the parameters (the weight vectors and biases) followed by successive updates to those parameters based on gradient descent until the error function \(E(X, \theta)\) converges.
A major advantage of gradient descent is that it can be used for online learning, since the parameters are not solved in one calculation but are instead gradually improved by moving in the direction of the negative gradient. Thus, if input-output pairs are arriving in a sequential fashion, the ANN can perform gradient descent on one input-output pair for a certain number of steps, and then do the same once the next input-output pair arrives. For an appropriate choice of step size \(\eta\), this approach can yield results similar to gradient descent on the entire dataset \(X\) (known as batch learning).
Because gradient descent is a local method (the step direction is determined by the gradient at a single point), it can only find local minima. While this is generally a significant problem for most optimization applications, recent research has suggested that finding local minima is not actually an issue for ANNs, since the vast majority of local minima are evenly distributed and similar in magnitude for large ANNs.
Backpropagation
For a long time, calculating the gradient for ANNs was thought to be mathematically intractable, since ANNs can have large numbers of nodes and very many layers, making the error function \(E(X, \theta)\) highly nonlinear. However, in the mid-1980s, computer scientists were able to derive a method for calculating the gradient with respect to an ANN's parameters, known as backpropagation, or "backpropagation by errors". The method works for both feedforward neural networks (for which it was originally designed) as well as for recurrent neural networks, in which case it is called backpropagation through time, or BPTT. The discovery of this method brought about a renaissance in artificial neural network research, as training non-trivial ANNs had finally become feasible.
References
- , D. Neuralnetwork. Retrieved June 4, 2005, from https://commons.wikimedia.org/wiki/File:Neuralnetwork.png
- , G. Microglia_and_neurons. Retrieved July 25, 2005, from https://commons.wikimedia.org/wiki/File:Microglia_and_neurons.jpg
- , B. Current_Clamp_recording_of_Neuron. Retrieved October 6, 2006, from https://commons.wikimedia.org/wiki/File:Current_Clamp_recording_of_Neuron.GIF
- , L. Heaviside. Retrieved August 25, 2007, from https://commons.wikimedia.org/wiki/File:Heaviside.svg
- , M. Linearna_separovatelnost_v_prikladovom_priestore. Retrieved December 13, 2013, from https://commons.wikimedia.org/wiki/File:Linearna_separovatelnost_v_prikladovom_priestore.png
- , Q. Logistic-curve. Retrieved July 2, 2008, from https://commons.wikimedia.org/wiki/File:Logistic-curve.svg
- , C. ArtificialNeuronModel. Retrieved July 14, 2005, from https://commons.wikimedia.org/wiki/File:ArtificialNeuronModel.png