System of Linear Equations (Simultaneous Equations)
A system of linear equations is a collection of linear equations which involve the same set of variables. As an example,
\[ \begin{align} x+2y & =2 \\ -x+y & =1 \end{align} \]
is a system of equations that has two variables \(x\) and \(y.\) The solution to a linear system is an assignment of numbers to the variables that satisfy every equation in the system. For a given system, we could have one solution, no solutions or infinitely many solutions.
Contents
Types
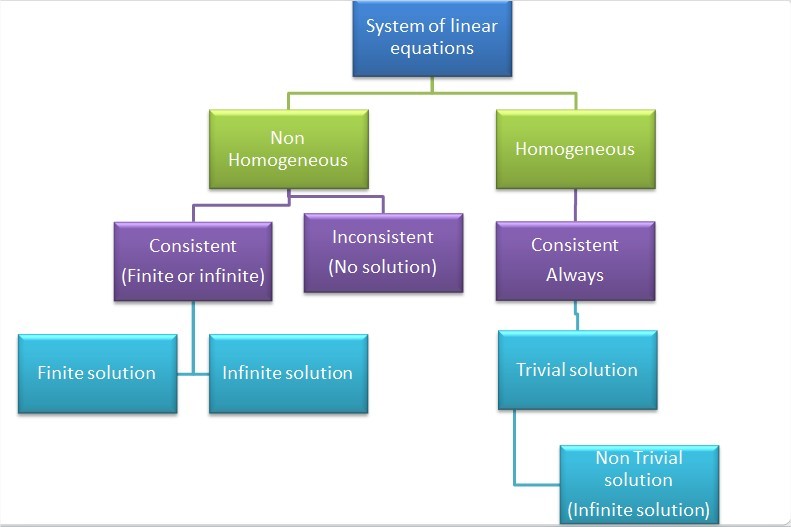
The system of linear equations are shown in the figure bellow:\[\]
 \[\]
\[\]
- Inconsistent: If a system of linear equations has no solution, then it is called inconsistent.
- Consistent: If a system of linear equations has at least one solution, then it is called consistent.
- Homogeneous system of equations: If the constant term of a system of linear equations is zero, i.e. the value after the "=" sign is zero, then it is called the homogeneous system of equations.
- Trivial and non-trivial solutions: Every homogeneous system of equations has a common solution and that is zero because they have a common solution for all variables, which is 0. This solution is called the trivial solution. If there are other solutions, then they are called non-trivial solutions.
We will explore how to solve a system of linear equations using the substitution and elimination methods.
Substitution Method
In this method, we
- find a relation that isolates one of the variables by changing the subject;
- substitute the relation into the other equation(s) to reduce the number of variables by 1;
- repeat until we are left with a single variable, and solve for it;
- substitute the solved value back into the relations;
- state the complete solution.
Let's follow the above steps to solve the following system of equations:
\[\begin{align} x+y &= 5 \\ x-y &= 3. \end{align}\]
Step 1: Isolate variable \(x\) using the second equation: \( x = 3 + y \).
Step 2. Substitute the relation into the other equation: \( (3 + y ) + y = 5 \Rightarrow 3 + 2y = 5 \).
Step 3. Repeat, and then solve. Since we now have only 1 variable, solve for it: \( 3 + 2y = 5 \Rightarrow y = \frac{5-3}{2} = 1 \).
Step 4. Substitute back into the relations: \( x = 3 + y = 3 + 1 = 4 \).
Step 5. State the complete solution: \( (x,y) = (4,1) \).
Solve the system of equations
\[ \begin{align} 2x + y &= 10\\ 2y &= 8 . \end{align}\]
In this example, because we are already given \( 2y = 8 \) in the second equation, we know that \( y = 4 \). Substituting this into the first equation, we get \( 2x + 4 = 10 \), and thus \( x = 3 \). \(_\square\)
Note: It matters which equation we use and which variable we isolate out. In this example, even if we obtained \( x = \frac{ 10 - y } { 2 } \) from the first equation, we find that we are unable to substitute it into the second equation as there is no \(x\) term.
Solve the system of equations
\[ \begin{align} 2x + y &= 4\\ 3x + 2y &= 7. \end{align}\]
Solving the first equation for \(y\) gives \(y=4-2x\). Substituting this into the second equation gives \[\begin{align} 3x + 2(-2x+4) &= 7\\ 3x -4x + 8 &= 7\\ -x & = -1\\ x & = 1. \end{align}\] Then substituting this value into the first equation, we have \[y=-2x + 4= -2(1) + 4 = -2 + 4 = 2.\] Therefore, the solution to the system of equations is \(x=1, y=2\). \(_\square\)
Using the process of substitution may not be the quickest nor the easiest approach for a given system of linear equations. However, we are always guaranteed to find the solution, if we work through the entire process. The word "system" indicates that the equations are to be considered collectively, rather than individually. Thus the solution must not lose validity for any of the equations. Select your options so that your calculations are simple and use any method that suits you.
Elimination Method
The elimination method multiplies the given \(n\) equations with suitable constants so that when the modified equations are added, one of the variables is eliminated. Once this is done, the system will have effectively been reduced by one variable and one equation. This process is repeated until one variable and one equation remain (namely, the value of the variable). From there, the obtained value is substituted into the equation with 2 variables, allowing a solution to be found for the second variable. The process is repeated until the values of all \(n\) variables are found.
Method
- Find two equations that have the same variable. Multiply each equation by a number such that their coefficients are equal.
- Subtract the two equations.
- Repeat until we are left with a single variable, and solve for it.
- Substitute the solved value back into the original equations to solve for the remaining variables.
Let's follow the above steps to solve the following system of equations:
\[\begin{align} 3x - 4y &= 0 \\ 9x - 8 y &= 12. \end{align}\]
Step 1: Multiply each equation by a number such that the coefficients of a variable are the same.
Let's say that we want to eliminate the variable \(x\).
Multiply the first equation by 3 and the second equation by 1, and we obtain
\[ 9 x - 12 y = 0, 9 x - 8 y = 12. \]Step 2: Subtract the two equations:
\[\begin{align} 9x - 12y &= 0 \\ - (9x - 8 y &= 12) \\ \hline -4 y & = - 12. \end{align} \]Step 3: Repeat and solve.
We are already down to one variable. Solving it gives us \( y = \frac{ -12}{-4} = 3 \).Step 4: Substitute the solved value back into the relations.
Substituting into the first equation, we get \( 3x - 4 \times 3 = 0 \Rightarrow x = \frac{12}{3} = 4 \).
System of Linear Equations - More Variables
When we have more variables to work with, we just have to remember to stick to a particular method, and keep on reducing the number of equations or variables.
We will solve the following system of equations using both approaches:
\[ \begin{align} x + 3y - z &= 6\\ 2x - y + 2z &= 1\\ 3x + 2y - z &= 2. \end{align}\]
Substitution method
We begin with the first of the above three equations:
- Step 1: The first equation gives \(x+3y-z=6 \Rightarrow x=6-3y+z\).
- Step 2: Substituting for \(x\) in the second equation, we obtain \[ \begin{align} 2(6-3y+z) - y + 2z &= 1\\ 12 - 6y + 2z - y + 2z &= 1\\ -7y + 4z &= -11. \qquad (1) \end{align}\] Substituting for \(x\) in the third equation, we obtain \[ \begin{align} 3(6-3y+z) + 2y - z & = 2\\ 18 - 9y + 3z + 2y - z &= 2\\ 2z - 7y &= -16. \qquad (2) \end{align}\]
- Step 3. We need to repeat until we have only one equation.
Now, we begin with \((1)\) of the two equations \((1)\) and \((2)\) above:
- Step 1: The equation \((1)\) gives us \( y = \frac{ 4z+11}{7} \).
- Step 2: Substituting for \(y\) in \((2)\) gives \[ \begin{align} 2z - 7 \frac{ 4z+11}{7}&= -16\\ 2z - ( 4z + 11 ) & = - 16 \\ -2z & = -5. \end{align}\]
- Step 3: We are now down to one equation. Solving it gives us \( z = \frac{-5}{-2} = \frac{5}{2} \).
- Step 4: Substitute \( z = \frac{5}{2} \) into \( y = \frac{ 4z + 11} { 7} \) to obtain \[ y = \frac{ 4z+ 11}{ 7} = \frac{ 4 \times \frac{5}{2} + 11 } { 7} = \frac{ 21}{7} = 3. \] Now, substitute \( z = \frac{5}{2}\) and \(y = 3 \) into \( x = 6 - 3y + z \) to obtain \[ x = 6 - 3 \times 3 + \frac{5}{2} = - \frac{1}{2}. \]
- Step 5: Hence, the solution is \[ (x,y,z) = \left( - \frac{1}{2}, 3, \frac{5}{2} \right). \ _\square \]
Elimination method
We are given the same system of linear equations as above: \[ \begin{align} x + 3y - z &= 6\\ 2x - y + 2z &= 1\\ 3x + 2y - z &= 2. \end{align}\]
Step 1: Let's eliminate \(x\) from the equations.
Step 2. Twice of the first equation minus the second is \[ \begin{align}
2(x + 3y - z &= 6)\\ -(2x - y + 2z &= 1)\\ \hline 7y - 4z & = 11. \qquad (4) \\\end{align} \] Thrice of the first equation minus the third is \[ \begin{align} 3(x + 3y - z &= 6)\\ -(3x + 2y - z &= 2)\\ \hline 7y - 2z & = 16. \qquad (5) \\ \end{align} \]We need to repeat till we just have one variable.
Step 1. Let's eliminate \( y \) from the equations.
Step 2. The fourth equation minus the fifth is \[ \begin{align} 7y - 4z & = 11 \\ - ( 7y - 2z & = 16 ) \\ \hline -2z & = - 5. \qquad (6) \\ \end{align} \]
Step 3. We are now down to one variable. Solving it gives us \( z = \frac{-5}{-2} = \frac{5}{2} \).
Step 4. Substitute \( z = \frac{5}{2} \) into the fourth equation \( 7y - 4z = 11 \) to obtain \[ y = \frac{ 4z+ 11}{ 7} = \frac{ 4 \times \frac{5}{2} + 11 } { 7} = \frac{ 21}{7} = 3. \] Now, substitute \( z = \frac{5}{2} , y = 3 \) into the first equation \( x = 6 - 3y + z \) to obtain \[ x = 6 - 3 \times 3 + \frac{5}{2} = - \frac{1}{2}. \]
Step 5. Hence, the solution is \[ (x,y,z) = \left( - \frac{1}{2}, 3, \frac{5}{2} \right).\ _\square \]
Solve the following system of equations: \[\]
\[ \begin{align} x + 2y - 3z &= -3\\ 2x - 5y + 4z &= 13\\ 5x + 4y - z&= 5. \\ \end{align} \]
Let us start with the last equation. Solving for \(z\), we obtain
\[z = 5x + 4y - 5.\]
Substituting this into the second equation gives
\[ \begin{align} 2x - 5y + 4(5x + 4y - 5 ) &= 13 \\ 22x + 11y - 33 &= 0 \\ 2x + y - 3 &= 0. \end{align} \]
Substituting this into the first equation gives
\[ \begin{align} x + 2y - 3(5x + 4y - 5) &= -3 \\ x + 2y - 15x -12y + 15 + 3 &= 0 \\ -14x - 10y + 18 &= 0\\ -7x - 5y + 9 &= 0. \end{align} \]
Thus, we now have reduced our system into a pair of equations with two variables:
\[ \begin{align} 2x + y - 3 &= 0\\ -7x - 5y + 9 &= 0. \end{align} \]
Solving for \(y\) in the first equation, we get
\[ y = 3 - 2x. \]
Substituting this into the second equation gives
\[ \begin{align} -7x - 5(3-2x)+9&=0 \\ -7x-15 + 10x + 9 &= 0\\ 3x - 6 &= 0 \\ x &= 2. \end{align} \]
Hence,
\[y = 3 - 2\cdot2 = -1, z = 5\cdot2 + 4\cdot(-1) -5 = 1. \]
Thus, the values of \(x, y,\) and \(z\) which satisfy the given system of equations are \((2,-1,1). \ _\square \)
Elementary Row Operation or Gaussian Elimination Method
Main Article: Solving Linear Systems Using Matrices
Elementary row operation or Gaussian elimination is a popular method for solving system of linear equations. By this method, everyone can solve system of linear equations only by matrix row operations that you already know. The terms we need to know for this section are explained below.
Augmented Matrix:
An augmented matrix for a system of equations is a matrix of numbers in which each row represents the constants from one equation and each column represents all the coefficients for a single variable.Suppose the system of linear equation is \[\begin{align} x_{1} + 2x_{2} + 5x_{3}&=2\\ 3x_{1} + x_{2} + 4x_{3}&=1\\ 2x_{1} - 7x_{2} + x_{3}&=5. \end{align}\]
Then the augmented matrix of this system of linear equations is \(\begin{pmatrix} 1 & 2 & 5 &2 \\ 3 & 1 & 4 & 1\\ 2 & -7 & 1 & 5 \end{pmatrix}.\)
What are row echelon form, reduced row echelon form, and leading 1?
The matrix is in reduced row echelon form \(\begin{pmatrix} 1 & 0 & 0 &1 \\ 0 & 1 & 0 & 2\\ 0 & 0 & 1 & 2 \end{pmatrix}.\)
To be of this form, a matrix must have the following properties:
- If a row does not consist entirely of zeros, then the first nonzero number in the row is a 1. We call this a leading 1.
- If there are any rows that consist entirely of zeros, then they are grouped together at the bottom of the matrix.
- In any two successive rows that do not consist entirely of zeros, the leading 1 in the lower row occurs farther to the right than the leading 1 in the higher row.
- Each column that contains a leading 1 has zeros everywhere else in that column.
A matrix that has the first three properties is said to be in row echelon form. If that matrix has the \(4^\text{th}\) property, then it's called reduced row echelon form.
Changing a matrix into row echelon form by elementary row operation:
A matrix can be changed to its reduced row echelon form, or row reduced to its reduced row echelon form using the elementary row operations, which are as follows:
- Interchange one row of the matrix with another of the matrix.
- Multiply one row of the matrix by a nonzero scalar constant.
- Replace the one row with the one row plus a constant times another row of the matrix.
Suppose that a system of linear equation is \[\begin{align*} x_{1} + 2x_{2} + 2x_{3}&=4\\ x_{1} + 3x_{2} + 3x_{3}&=5\\ 2x_{1} + 6x_{2} + 5x_{3}&=6, \end{align*}\]
and its augmented matrix is \(\begin{pmatrix} 1 & 2 & 2 &4 \\ 1 & 3 & 3 & 5\\ 2 & 6 & 5 & 6 \end{pmatrix}.\)
Now, we'll apply elementary row operation on this matrix and convert it to reduced row echelon form:
\[\begin{align} &\Rightarrow\begin{pmatrix} 1 & 2 & 2 &4 \\ 0 & 1 & 1 & 1\\ 2 & 6 & 5 & 6 \end{pmatrix}-1R_{1}+R_{2}\\ \\ &\Rightarrow \begin{pmatrix} 1 & 2 & 2 &4 \\ 0 & 1 & 1 & 1\\ 0 & 2 & 1 & -2 \end{pmatrix}-2R_{1}+R_{3}\\ \\ &\Rightarrow\begin{pmatrix} 1 & 2 & 2 &4 \\ 0 & 1 & 1 & 1\\ 0 & 0 & -1 & -4 \end{pmatrix}-2R_{2}+R_{3}\\ \\ &\Rightarrow\begin{pmatrix} 1 & 2 & 2 &4 \\ 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 4 \end{pmatrix}-1R_{3}. \end{align}\]
Finally the matrix is in the row echelon form: \(\begin{pmatrix} 1 & 2 & 2 &4 \\ 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 4 \end{pmatrix}. \)
So, at last we get the reduced form of the system of linear equation, which is \[\begin{align*} x_{1} +2x_{2}+2x_{3} &= 4\\ x_{2}+x_{3}&=1 \\ x_{3} &= 4. \end{align*}\] By solving this, we get \[\begin{align*} x_{1}&= 2\\ x_{2} &=-3 \\ x_{3} &= 4. \end{align*}\]
Md Nur Uddin is a student of Mathematics Discipline Of Khulna University. Now, you have to find his student ID by solving the following system of linear equations:
\[\begin{align*} -3x+2y-6z &=6 \\ 5x+7y-5z &=6 \\ x+4y-2z &=8. \end{align*}\]
If the solution satisfies \(x+y=z,\) what is the value of \(x+y,\) or equivalently \(z?\)
System of Linear Equations Word Problems - Basic
System of Linear Equations Word Problems - Intermediate
The brothers Luiz and Lucio bought a land surrounded by a wall of \(340 \text{ meters} \). They built an inner wall to divide the land into two parts. Now, the part of Luiz is surrounded by a wall of \(260 \text{ meters} ,\) and the part of Lucio by a wall of \(240 \text{ meters} \). What is the length of the inner wall?

There was a thief who went to a wine shop to steal wine. He went in at 10 pm, stole 15 L of wine and added 15 L of water to top up the barrel. He came back at 1 am, stole 15 L of the mixture from the same barrel and added 15 L of water to top it up. He came back at 4 am, stole 15 L of the mixture from the same barrel and added 15 L of water to top it up. In the morning, the ratio of wine to water in the barrel was 343:169. Find the initial amount of wine in the barrel.
System of Linear Equations - Problem Solving
The solutions of the system of equations
\[3x−y=a, \qquad x+y=5\] are the same as those of the system of equations \[2x+y=24, \qquad x−3y=b.\]
What is the value of \(a+b\)?
Since the two systems of equations have the same solutions, we first use substitution to find the solutions to the simultaneous equations
\[x+y=5, \qquad 2x+y=24.\]
Solving the first equation for \(y\) gives \(y=5-x\) and plugging into the second equation gives \(2x + (5-x) = 24\), or \(x = 19\). Plugging this into the first equation gives \(19+y=5\), or \(y=-14\). Thus, \(x=19\) and \( y=−14. \) Substituting these values into \(3x−y=a\) gives
\[a=3x−y=3×19−(−14)=71.\]
Similarly, substituting into \(x−3y=b\) gives
\[b=x−3y=19−3×(−14)=61.\]
Therefore, \[a+b=71+61=132. \ _\square\]