Thermal Expansion
It is a characteristic property of any substance that when heat is supplied to them they will expand. In this wiki, we will study the expansion of substances in different situations.
You may have observed that sometimes sealed bottles with metal lids are so tightly screwed that one has to put the lid in hot water for sometime to open the lid. The reason we do this is that it would allow the metallic cover to expand, thereby loosening it to unscrew easily. In case of liquids, you may have observed that mercury in a thermometer rises when the thermometer is put in a slightly warm water. If we take out the thermometer from the warm water, the level of mercury falls again. Similarly, in case of gases, a balloon partially inflated in a cold room may expand to full size when placed in warm water. On the other hand, a fully inflated balloon when immersed in cold water would start shrinking due to contraction of the air inside.
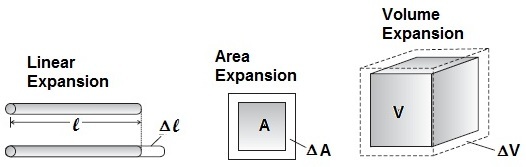
It is our common experience that most of the substances expand on heating and contract on cooling. A change in the temperature of the body causes a change in its dimensions. The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion. The expansion in length is called linear expansion. The expansion in the area is called areal expansion. The expansion in volume is called volume expansion. In solids all these three types of expansions occur, while in liquids only volume expansion is possible. We will discuss them in separate sections.
Contents
Linear Expansion
Consider a rod of initial length \(l_\circ\) which is made up of a material with coefficient of linear expansion \(\alpha\).

If the rod is subjected to a rise in temperature \(\triangle T,\) the length of the rod increases and the new final length \(l\) is given by
\[l = l_\circ(1 + \alpha \triangle T).\]
The change in length of the rod \(\triangle l = l - l_\circ\) is given by
\[\triangle l = l_\circ \alpha \triangle T.\]
The coefficient of linear expansion is the characteristic of the material of the rod and varies from material to material. Its SI unit is \(K^{-1}\). It is generally in the order of \(10^{-5}\). The \(\alpha\) values of some materials in the temperature range of \(0^\circ\) to \(100^\circ\) are given in the table below:
\[\begin{array} {| c | c |} \hline \ {\color{blue}\text{Material}} & {\color{green}\alpha ~ \big(10^{-5} K^{-1}\big)} \\ \hline \ \text{Aluminum} & 2.5 \\ \hline \ \text{Brass} & 1.8 \\ \hline \ \text{Iron} & 1.2 \\ \hline \ \text{Copper} & 1.7 \\ \hline \ \text{Silver} & 1.9 \\ \hline \ \text{Gold} & 1.4 \\ \hline \ \text{Glass (Pyrex)} & 0.32 \\ \hline \ \text{Lead} & 0.29 \\ \hline \end{array}\]
From this table, compare the values of \(\alpha\) for glass and copper. We find that copper expands about five times more than glass does for the same rise in temperature. Normally, metals expand more than non-metals and have relatively high values of \(\alpha\).
Note: It is very important to note that if we take any two points on the same material, then change in length of those two points is given by \(\triangle l = l_0 \alpha \triangle T\), irrespective of whether between the two points there is a cavity or not. In other words, whether a cavity is present or not, expansion of body is not affected.
Let us consider two rods of length \(l_1\) and \(l_2\) which are made of different materials whose coefficients of linear expansion are \(\alpha_1\) and \(\alpha_2,\) respectively. For the difference between the two lengths to be independent of temperature,
\[ l_1\alpha_1 = l_2\alpha_2.\]
Given that the initial lengths are \(l_1\) and \(l_2,\) after increasing the temperature, let the new lengths be \(l'\) and \(l'',\) respectively. Then\[l' = l_1(1 + \alpha_1 \triangle T), \quad l'' = l_2(1 + \alpha_2 \triangle T).\]
Now, let's find the difference of the final lengths that is \(l' - l'':\)
\[\begin{align} l' - l'' &= l_1 + l_1\alpha_1\triangle T - l_2 - l_2\alpha_2\triangle T \\ &= ({\color{pink}l_1 - l_2}) + \triangle T(\color{blue}{l_1\alpha_1 - l_2\alpha_2}). \end{align}\]
For the difference of lengths to be independent of temperature, the \(\color{blue} \text{coefficient of } \triangle T\) must be \(0:\)
\[l_1\alpha_1 - l_2\alpha_2 = 0.\]
Therefore, the final condition we get is
\[l_1\alpha_1 = l_2\alpha_2.\ _\square\]
A blacksmith fixes an iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the rim and the iron ring are \(5.243\text{ m}\) and \(5.231\text{ m},\) respectively, at \(27\, ^\circ\text{C}.\) To what temperature should the ring be heated so as to fit the rim of the wheel? Take \(\alpha_{\text{iron}} = 1.2 \times 10^{-5}~K^{-1}.\)
We are given \(T_1 = 27\, ^\circ\text{C}, l_\circ = 5.231, l = 5.243\). So,\[\begin{align} l & = l_\circ(1 + \alpha \triangle T) \\ & = 5.231\big(1 + 1.2 \times 10^{-5} (T - 27)\big) \\ \\ \Rightarrow & T = 218\, ^\circ\text{C}.\ _\square \end{align}\]
How much should the temperature of a brass rod be increased for the length to increase by 1%, given that \(\alpha_{\text{brass}} = 0.00002 /^\circ\text{C}?\)
If the length is increased by 1%, it implies that \(\triangle l = \frac{1}{100}l_\circ\). We know that\[\begin{align} \triangle l & = l_\circ \alpha \triangle T \\ \dfrac{1}{100}l_\circ & = l_\circ \alpha \triangle T \\ \\ \Rightarrow \triangle T & = \dfrac{1}{100\alpha} \\\\ & = \dfrac{1}{2 \times 10^{-3}} \\\\ & = 500\,^\circ\text{C}.\ _\square \end{align}\]
A composite rod is a rod which is made up by joining two or more rods of different materials end to end. The below example is based on a composite rod:
A brass rod of length \(50\text{ cm}\) and diameter \(3.0\text{ mm}\) is joined end to end to a steel rod of the same length and diameter, at \(40\, ^\circ\text{C}.\) What is the change in the length of the combined rod at \(250\, ^\circ\text{C},\) given \(\alpha_{\text{brass}} = 2 \times 10^{-5} /^\circ\text{C}, \alpha_{\text{steel}} = 1.2 \times 10^{-5} /^\circ\text{C}?\)
We have\[\begin{align} \triangle L_{\text{combined}} & = \triangle L_{\text{brass}} + \triangle L_{\text{steel}} \\ & = \alpha_b L_b \triangle T + \alpha_s L_s \triangle T \\ & = (\alpha_b L_b + \alpha_s L_s) \triangle T \\ & = \big(2 \times 10^{-5} \times 0.5 + 1.2 \times 10^{-5} \times 0.5\big)(250 - 40) \\ & = 0.0034\text{ m} = 0.34\text{ cm}.\end{align}\]
Therefore, the new length of the combined rod is \(50 + 50 + 0.34 = 100.34\text{ cm}.\) \(_\square\)
Two identical circular holes are made in a metallic square sheet, and two tiny points \(A\) and \(B\) are marked next to the holes, as shown in the diagram.
If the temperature of the whole sheet is uniformly raised, then the size of the holes will \(\text{__________}\) and the distance between \(A\) and \(B\) will \(\text{__________}.\)


The left photo is an expansion joint in a road bridge used to avoid damage from thermal expansion. Thermal expansion is the tendency of matter to change in volume in response to a change in temperature.
The photo on the right is an iron plate with a hole in it.
If this iron plate is heated, will the size of the hole grow or shrink?
Areal Expansion
Consider a body of surface area \(A_\circ\) which is made up of a material of coefficient of areal expansion \(\beta\).
If the body is subjected to a rise in temperature \(\triangle T,\) the surface area of that body increases and the new surface area \(A\) is given by
\[A = A_\circ(1 + \beta \triangle T).\]
The change in the surface area of the body \(\triangle A = A - A_\circ\) is given by
\[\triangle A = A_\circ \beta \triangle T.\]
Volume Expansion
Consider a substance of volume \(V_\circ\) which is made up of a material of coefficient of volume expansion \(\gamma\).
If the body is subjected to a rise in temperature \(\triangle T,\) the volume of that body increases and the new volume \(V\) is given by
\[V = V_\circ(1 + \gamma \triangle T).\]
The change in volume of the body \(\triangle V = V - V_\circ\) is given by
\[\triangle V = V_\circ \gamma \triangle T.\]
Note: When any body is heated, the mass of the body does not change. But the volume changes. To compensate this, the density of the body also changes:
\[\begin{align} m & = Vd ~ (\text{constant}) \\ V_1d_1 & = V_2d_2 \\ V_\circ d_\circ & = V_\circ(1 + \gamma \triangle T)d \\ \Rightarrow d &= \dfrac{d_\circ}{1 + \gamma \triangle T}.\\ \end{align}\]
Isotropic Substances
An isotropic substance is a substance for which
\[\boxed{\gamma = \dfrac32 \beta = 3 \alpha},\]
where \(\alpha, \beta, \gamma\) are the coefficients of linear expansion, areal expansion, and volume expansion, respectively. It can also be written as
\[\beta = 2 \alpha, \quad \gamma = 3 \alpha.\]
The volumes of a thin brass vessel and a solid brass cube are both 1 liter at \(0\, ^\circ\text{C}\). What will be the change in the volumes of the vessel and solid cube at \(25\, ^\circ\text{C}, \) given \(\alpha_{\text{brass}} = 1.9 \times 10^{-5}/^\circ\text{C}?\)
We have\[\begin{align} \triangle V & = V_o (\gamma) \triangle T \\ & = V_o (3\alpha) \triangle T \\ & = 1 \times 3 \times 1.9 \times 10^{-5} \times (25 - 0) \\ & = 0.001425\ \text{ liter}.\ _\square \end{align}\]
Consider a vessel containing some liquid. When we heat it, not only the liquid but also the glass or metal container will expand. Actually, if the container is not expandable, then we will see more rise in the liquid level. This is called real expansion. But because of container expansion, it can accommodate more liquid in its back, and the level of liquid rise will be less. This is called apparent expansion. We can write a relation in apparent expansion as
\[\begin{align} \triangle V_{\text{app}} & = \triangle V_{\text{liquid}} - \triangle V_{\text{container}} \\ V_o \gamma_{\text{app}} \triangle T & = V_o \gamma_{\text{l}} \triangle T - V_o \gamma_{\text{g}} \triangle T \\ \gamma_{app} & = \gamma_{\text{l}} - \gamma_{\text{g}},\end{align}\]
where \(\gamma_{\text{app}}\) is the apparent coefficient of expansion, \(\gamma_{\text{l}}\) is the real coefficient of expansion (of the liquid), and \(\gamma_{\text{g}}\) is the coefficient of expansion of the glass (or any other metal) container.
The volume of a glass vessel filled with mercury is 500 cc. What volume of mercury will overflow when the temperature is increased from \(25^\circ C\) to \(45^\circ C,\) given \(\gamma_{Hg} = 1.8 \times 10^{-4}/^\circ\text{C}, \gamma_g = 9 \times 10^{-6}/^\circ\text{C}?\)
We have\[\begin{align} \triangle V_{\text{flow out}} & = \triangle V_{\text{Hg}} - \triangle V_{\text{g}} \\ & = V_o \gamma_{\text{Hg}} \triangle T - V_o \gamma_{\text{g}} \triangle T \\ & = V_o (\gamma_{\text{Hg}} - \gamma_{\text{g}}) \triangle T \\ & = 500 \times (180 - 9) \times 10^{-6} \times 20 \\ & = 1.71\text{ cc}.\ _\square \end{align}\]

Professor \(\mathfrak{X}\) is a very ingenious scientist and researcher.
Once Professor \( \mathfrak{X}\) was doing some experiments in his laboratory related to heat and thermal expansion. He took a metal ball and heated it until its temperature increased by \( 30\ ^{\circ}\text{C}.\) Then he found that the volume of the metal ball increased by \( 0.18\%\).
Assuming isotropic behavior of the metal ball, calculate the coefficient of linear expansion of the metal and help Professor \(\mathfrak{X}\) in his research.
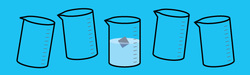
A metallic cube is floating inside a beaker. The temperature of the system is increased by a small amount ΔT. It is found that the depth of the submerged portion of the cube does not change. Then the ratio of the coefficient of linear expansion of the cube and the coefficient of volume expansion of the liquid is given by \(\frac{a}{b},\) where \(a\) and \(b\) are coprime positive integers.
What is \(a+b?\)
Note: Ignore the expansion of the beaker.
Time Period of Pendulum
A pendulum will show the correct time only when it is operated at a temperature where it is manufactured. The time period of a pendulum is a function of temperature. That means the time period varies with a change in temperature. The reason behind this is that the length of the pendulum wire being made of metal changes its length with changes in temperatures. However, the error in time can be calculated.
The error in time \(\triangle t\) over a time period of \(t_\circ\) is given by
\[\triangle t = \dfrac{t_\circ \alpha \triangle T}{2},\]
where \(\alpha\) is the coefficient of linear expansion of the wire of pendulum and \(\triangle T\) is the change in temperature.
Let us consider a pendulum whose initial length is \(l_\circ\). The initial time period of the pendulum is given by \(t_\circ = 2 \pi \sqrt{\frac{l_\circ}{g}}\). If the temperature is increased by \(\triangle T,\) then the final length of the pendulum will be \(l = l_\circ(1 + \alpha \triangle T)\) and its time period \(t = 2 \pi \sqrt{\frac{l}{g}}\). So, the error in the time \(\triangle t\) will be \((t - t_\circ):\)\[\begin{align} t & = 2 \pi \sqrt{\dfrac{l}{g}} \\ & = 2 \pi \sqrt{\dfrac{l_\circ(1 + \alpha \triangle T)}{g}} \\ & = {\color{blue}2 \pi \sqrt{\dfrac{l_\circ}{g}}} (1 + \alpha \triangle T)^\frac12 \\ & = {\color{blue}t_\circ} \left(1 + \dfrac12 \alpha \triangle T \right) \qquad \qquad (\text{As } \alpha \triangle T \text{ is very small, we can use binomial approximation.}) \\\\ t - t_\circ & = \dfrac{t_\circ \alpha \triangle T}{2} \\ \\ \Rightarrow \triangle T & = \dfrac{t_\circ \alpha \triangle T}{2} \quad \text{or} \quad \dfrac{\triangle T}{t_\circ} = \dfrac{\alpha \triangle T}{2}.\ _\square \end{align}\]
- If temperature is less \(\implies\) time period will be less \(\implies\) clock will run faster \(\implies\) clock will gain time.
- If temperature is more \(\implies\) time period will be more \(\implies\) clock will run slower \(\implies\) clock will loose time.
A clock has pendulum made of brass, and it is adjusted to have a period of 1 second at \(20\, ^\circ\text{C}\). If the clock is operated at \(30\, ^\circ\text{C},\) what will be the error after 1 week, given \(\alpha_{\text{brass}} = 19.6 \times 10^{-6}/^\circ\text{C}?\)
We have\[\begin{align} \dfrac{\triangle t}{t} & = \dfrac12 \alpha \triangle T \\ \triangle t & = \dfrac12 \alpha \triangle T \cdot t \\ & = \dfrac12 \times 19.6 \times 10^{-6} \times 10 \times \underbrace{7 \times 86400}_{\text{1 week}} \\ & = 59.32\ \text{ seconds}\\\\& \approx 1\ \text{ minute}.\ _\square \end{align}\]
A brass clock keeps correct time at a certain \(T.\) How close the \(T\) should be controlled so that the watch should not gain or loose 1 second in a day, given \(\alpha_{\text{brass}} = 2 \times 10^{-5}/^\circ\text{C}?\)
Given \(t = 1\text{ day} = 86400\text{ seconds}\) and \(\triangle t = \dfrac{t}{2} \alpha \triangle T,\)\[\begin{align} |\triangle t| & \leq 1\text{ second} \\ \left | \dfrac{t}{2} \alpha \triangle T \right | & \leq 1 \\ \dfrac12 \times 86400 \times 2 \times 10^{-5} \times |\triangle T| & \leq 1 \\ |\triangle T| & \leq 1.15\, ^\circ\text{C}.\ _\square \end{align}\]
Metallic Scale Readings and Bimetallic Strip
A metallic scale shows correct reading only when it is used at its manufactured temperature. When it is used at all temperatures, it may either show less than actual reading (due to contraction) or it may show more than actual reading (due to expansion). Generally, a metallic scale expands on heating. As a result, all the markings are displaced from their usual correct positions. So, if a scale shows the length of some object as 10 cm when used at higher temperatures, we should understand that it is \(10(1 + \alpha \triangle T)\text{ cm}\) and vice versa if the temperature is low. So,
\[\text{(Actual length) = (Scale reading)}\times (1 + \alpha \triangle T).\]
A meter scale is made of steel and is calibrated at \(20\, ^\circ\text{C}.\) Find the distance between 50 cm and 51 cm if the scale is used at \(10\, ^\circ\text{C},\) given \(\alpha_{\text{steel}} = 1.1 \times 10^{-5}/^\circ\text{C}.\)
We have\[\begin{align} \text{(Actual length)} & = l_o(1 + \alpha \triangle T) \\ & = 1\big(1 + 1.1 \times 10^{-5} \times (-10)\big) \\ & = 1\big(1 - 11 \times 10^{-5}\big) \\ & = 1 - 0.00011 \\ & = 0.99989\text{ cm}.\ _\square \end{align}\]
Bimetallic Strip:
If two strips of equal length but different metals are placed on each other and riveted, the single strip so formed is called a bimetallic strip. This strip has the characteristic property of bending on heating due to the unequal linear expansion of the two metals. The strip will bend with the metal of greater coefficient of linear expansion on the outer side (or convex side). This strip finds its application in auto cut or thermostat in electric heating circuits like electric iron.
A metal strip of length \(l_0 = 20 \,\text{cm}\) consists of a layer of iron (Fe) and a layer of zinc (Zn), which are welded together with each having a thickness of \(d = 2\,\text{mm}\). At a temperature of \(T = 0\, ^\circ\text{C}\), the bimetallic strip is completely straight.
What is the radius of the curvature \(r\) of the strip at a temperature of \(T = 100\, ^\circ\text{C}?\)
The respective thermal expansion coefficients of zinc and iron are
\[\alpha_\text{Zn} = 3\cdot 10^{-5}/^\circ\text{C},\quad \alpha_\text{Fe} = 1\cdot 10^{-5}/^\circ\text{C}.\]

Two straight metallic strips each of thickness \(t\) and length \(l\) are riveted together. Their coefficients of linear expansion are \(\alpha_1 \) and \(\alpha_2\). If they are heated through a temperature of \(\Delta t\), the bimetallic strip will bend to form an arc of radius \(r.\)
Find \(r.\)
- (a) \(\ \dfrac t{(\alpha_1 + \alpha_2) \Delta t} \)
- (b) \(\ \dfrac t{(\alpha_2-\alpha_1) \Delta t} \)
- (c) \(\ {(\alpha_1+\alpha_2) \Delta t} \)
- (d) \(\ {(\alpha_2-\alpha_1) \Delta t} \)
Type 1 for option (a), 2 for option (b), 3 for option (c), or 4 for option (d).