Traversals
A tree traversal, also known as tree searches, are algorithms executed on graphs containing only tree edges, that visit each node exactly once. Algorithms in this category differ only in the order in which each node is visited. Two classic methods to traverse a tree are breadth-first search (bfs), where nodes in the same level or distance away from the root are visited before proceeding to the next level; and depth-first-search, where all the nodes in a branch, or one set path from root to leaf, are visited before passing on to the next branch. Other methods exist that use heuristics or random sampling to move through a tree as a way to speed up the process.
 Roots, trees, and branches are the basic parts of a tree data structure.
Roots, trees, and branches are the basic parts of a tree data structure.
Note: Binary trees are most often used in order to illustrate tree traversals, yet solutions can be generalized to all trees. It is also assumed that nodes on the left precede nodes on the right, but this can be reversed given proper consistency.
Contents
Traversing a Tree
Unlike an array or a list of numbers which are designed to be processed in order, trees do not present a linear configuration of elements; instead, processing can occur at a given node or at any of a node’s children.
Since this type of algorithm has to select the next node to be processed when traversing down a tree, the algorithm must remember the nodes it doesn’t visit in order to explore them later. To achieve this purpose, algorithms employ either a stack, where the most recently stored node has priority; or a queue, where the first item stored in the array has the highest priority. These techniques are commonly executed using recursion, which allows for a short amount of instructions, or lines of code. The particular technique used depends on the desired purpose, whether it be solving search, divide and conquer, or graph theory problems, amongst many others.
A queue is treated like a line of people, where the first one to come is the first one to be served. This data storage technique is also called FIFO, or first in first out. On the other hand, think of a stack as a stack of plates, where the last one on top is the first one being used. This is also called LIFO, or last in first out.
 Think of a queue as a line of people, and a stack as a pile of plates.[1][2]
Think of a queue as a line of people, and a stack as a pile of plates.[1][2]
Depth-first Search
Depth-first search, or DFS, is the strategy that goes down a branch all the way until a leaf is reached, processes said branch, and then moves on to a different branch. This type of algorithm generally uses a stack in order to keep track of visited nodes, as the last node seen is the next one to be visited and the rest are stored to be visited later.
Pseudocode[3]
Initialize an empty stack for storage of nodes, S. For each vertex u, define u.visited to be false. Push the root (first node to be visited) onto S. While S is not empty: Pop the first element in S, u. If u.visited = false, then: U.visited = true for each unvisited neighbor w of u: Push w into S. End process when all nodes have been visited.Python Implementation without Recrusion
def depht_first_search(graph): visited, stack = set(), [root] while stack: vertex = stack.pop() if vertex not in visited: visited.add(vertex) stack.extend(graph[vertex] - visited) return visited
DFS can also be implemented using recursion, which greatly reduces the number of lines of code.
Python Implementation Using Recursion
def depth_first_search_recursive(graph, start, visited=None): if visited is None: visited = set() visited.add(start) for next in graph[start] - visited: depth_first_search_recursive(graph, next, visited) return visited
It is common to modify the algorithm in order to keep track of the edges instead of the vertices, as each edge describes the nodes at each end. This is useful when one is attempting to reconstruct the traversed tree after processing each node. In case of a forest, or a group of trees, this algorithm can be expanded to include an outer loop that iterates over all trees in order to process every single node.
 Animated Depth-first Search Algorithm [4]
Animated Depth-first Search Algorithm [4]
There are three different strategies for implementing DFS: pre-order, in-order, and post-order.
Pre-order DFS works by visiting the current node, and successively moving to the left until a leaf is reached, visiting each node on the way there. Once there are no more children on the left of a node, the children on the right are visited. This is the most standard DFS algorithm.
Instead of visiting each node as it traverses down a tree, an in-order algorithm finds the left-most node in the tree, visits that node, and subsequently visits the parent of that node. It then goes to the child on the right and finds the next left-most node in the tree to visit.
A post-order strategy works by visiting the leftmost leaf in the tree, then going up to the parent and down the second left-most leaf in the same branch, and so on until the parent is the last node to be visited within a branch. This type of algorithm prioritizes the processing of leafs before roots in case a goal lies at the end of a tree.
The head of recruitment at a paper processing company needs to know how many potential candidates are being contacted at each targeted university. Since the company is just starting out, they don’t have the software tools necessary to keep track of this; therefore, she decides to use what she knows about depth-first search algorithms and starts this count by asking all the employees in charge of specific regions for the number of people they are talking to. These regional employees then ask the workers in charge of specific schools for a head count. What depth-first search strategy is the head of recruitment using to get a headcount of potential recruits?

The depth-first search algorithm is applied profusely in the field of graph theory: when finding the shortest paths, detecting a cycle, finding connected components, sorting a tree, or finding the exit or goal in a maze.
Breadth-first Search
Breadth-first search, or BFS, is the counterpart to DFS in tree traversing techniques. It is a search algorithm that traverses down a tree using a queue as its data array, where elements are visited in a FIFO--first in first out--mechanism. This strategy is also called level-order traversal, as all nodes on a level are visited before proceeding to the next level.
The pseudocode for BFS is exactly the same as that for DFS, except that a queue is utilized instead of a stack to store unvisited nodes. This changes the order of visited nodes as the first one in to be stored, chronologically, has the highest priority to be visited next. In other words, BFS visits all of a node’s neighbors before moving on to the neighbor’s neighbors.
Pseudocode[3]
Initialize an empty queue for storage of nodes, S. For each vertex u, define u.visited to be false. Push the root (first node to be visited) onto S. While S is not empty: Pop the last element in S: u. If u.visited = false, then: U.visited = true for each unvisited neighbor w of u: Push w into S. End process when all nodes have been visited.Python Implementation
def breadth_first_search(graph): visited, queue = set(), [root] while queue: vertex = queue.pop(0) if vertex not in visited: visited.add(vertex) queue.extend(graph[vertex] - visited) return visited
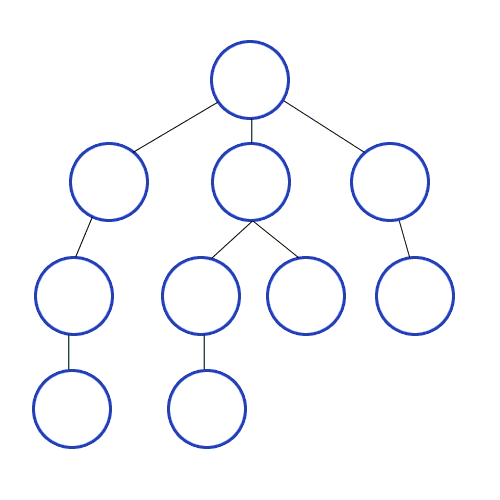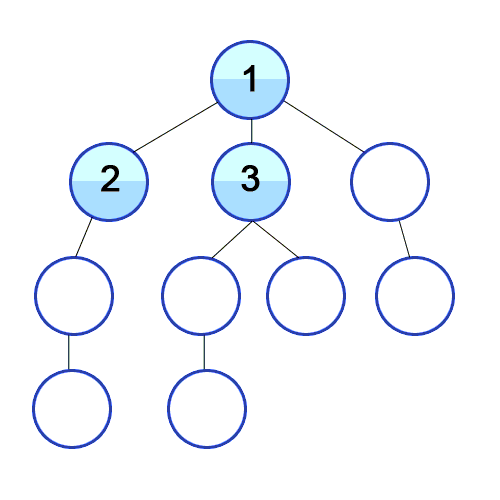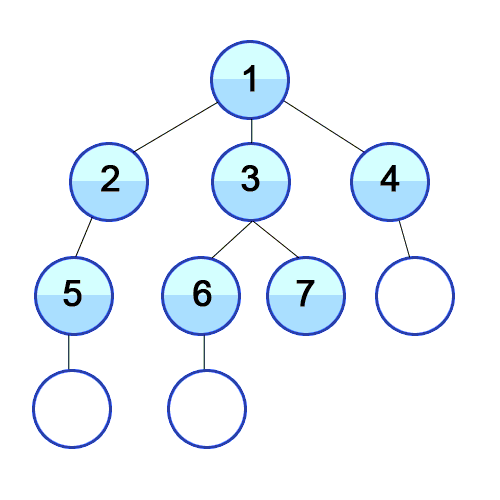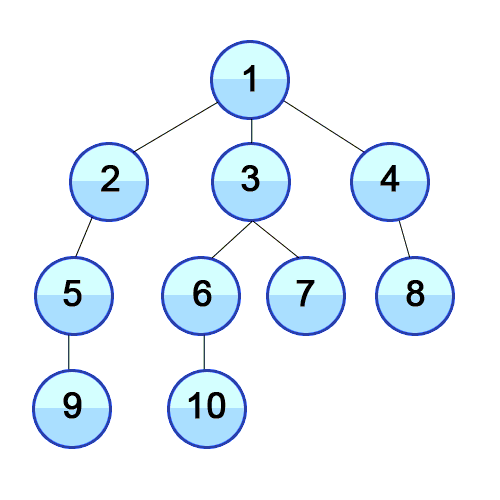 Animated Breadth-first search algorithm. [5]
Animated Breadth-first search algorithm. [5]
Alternative Traversal Techniques
Other algorithms have been developed that traverse a tree without using either BFS or DFS. These algorithms include the Monte-Carlo tree search, which utilizes random sampling to traverse a tree; as well as many other graph search algorithms which attempt to find a given destination quickly and efficiently using additional information. These include the hill climbing algorithm, beam search algorithm, branch and bound algorithm, and the A* algorithm, all of which use heuristics or other graph insights, to determine the best next step in the traversing.
Another example of a tree traversal problem are infinite trees, where there are virtually infinite number of nodes. These types of trees represent problems with enormous complexity space, such as a computer playing chess or the recently developed computer that plays the game of Go. These problems present difficulties to simple DFS and BFS implementations, as the algorithms may never visit the end of a branch given an implementation using DFS, or may never visit every single branch given an implementation using BFS.
For more tree traversal applications in computer science, refer to Konig’s infinity lemma, the travelling salesman problem, Cheney’s algorithm, or Ford Fulkerson’s algorithm.
References
- Stone E Soup, J. reduce. reuse. recycle. how the 3Rs can help you with the washing up. Retrieved from http://thestonesoup.com/blog/2011/01/reduce-reuse-recycle-how-the-3rs-can-help-you-with-the-washing-up/
- Pixabay, a. Line, People. Retrieved from https://pixabay.com/static/uploads/photo/2014/08/31/00/58/people-431943_960_720.jpg
- Heap, D. Depth-first search (DFS). Retrieved December 16th, 2002, from http://www.cs.toronto.edu/~heap/270F02/node36.html
- Wikimedia, M. Depth-First-Search.gif. Retrieved July 15, 2016, from https://commons.wikimedia.org/wiki/File:Depth-First-Search.gif
- Wikimedia, M. File:Depth-First-Search.gif. Retrieved from https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif)