Binary Search Trees

Binary search trees (also binary trees or BSTs) contain sorted data arranged in a tree-like structure. A binary tree consists of "root" and "leaf" data points, or nodes, that branch out in two directions.

Binary trees store "items" (such as numbers, names, etc.) in memory, allowing fast lookup, addition, and removal of items. They can be used to implement either dynamic sets of items or lookup tables that allow finding an item by its key. Binary trees and related variations have many practical uses such as in databases, for parsing syntax in a programming language, and in file compression.

Each tree starts with a single root node that contains data as well as references to left and right nodes. Each left and right nodes can also contain data and references to its own left and right nodes, respectively. This pattern continues recursively, forming a tree.

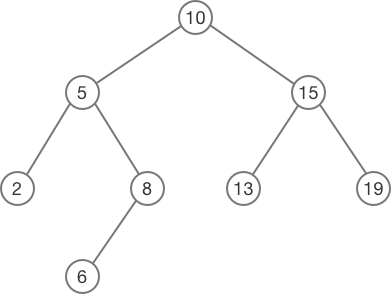Binary tree diagram

All of the code examples in this section are using a common class for the nodes of the binary tree:

1
2
3
4
5
6
7
8

class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value # information that is being stored in the tree
        self.left = left   # the left child (subtree)
        self.right = right # the right child (subtree)

    def __str__(self):
        return str(self.value)

Tree Traversal:

There are two primary ways to traverse, or iterate through, a tree: depth-first and breadth-first. In the depth-first method, the left subtree is searched first, then the right subtree is searched. In the breadth-first method, the search progresses through the nodes at each height level of the tree, or in other words, the root node first, then level 1 nodes, then level 2 nodes, and so forth.

Depth-first

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def b_list_depth_first(node):
    if not node:
        return []
    result = []
    if node.left:
        # append the left subtree's values
        result = result + b_list_depth_first(node.left)
    if node.value:
        # append this node's value
        result.append(node.value)
    if node.right:
        # append the right subtree's values
        result = result + b_list_depth_first(node.right)
    return result

Breadth-first

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def b_list_breadth_first(node):
    result = []
    nodelist = [node]
    # nodelist contains the nodes for height n
    while nodelist:
        # next_nodelist will contain the nodes for height n+1
        next_nodelist = []
        for subnode in nodelist:
            # append the current node's value to the result list
            result.append(subnode.value)
            # append the current node's children to next_nodelist
            if subnode.left:
                next_nodelist.append(subnode.left)
            if subnode.right:
                next_nodelist.append(subnode.right)
        nodelist = next_nodelist

    return result

Insertion:

To insert a node, find the leftmost leaf node that is less than the value being inserted. Add a child node to that node containing the inserted value.

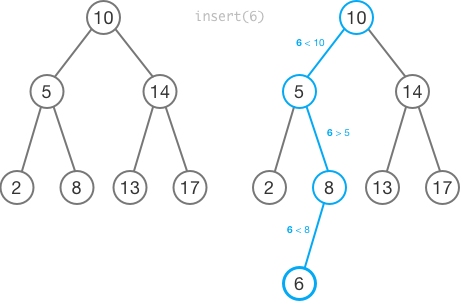The method for inserting a new value

1
2
3
4
5
6
7
8
9

def b_insert(node, value):
    if not node.value:
        node.value = value
    if value < node.value:
        node.left = node.left or Node()
        b_insert(node.left, value)
    elif value > node.value:
        node.right = node.right or Node()
        b_insert(node.right, value)

Deletion:

Deletion is less straightforward. There are three cases to consider:

• Case 1: If the deleted node has no children, remove the node from its parent.
• Case 2: If the deleted node has one child, replace the node with its child.
• Case 3: If the deleted node has two children, do the following:
  1. Start with the current node's right child.
  2. Find that child's leftmost child.
  3. Replace the current node's value with the leftmost child's value.
  4. Call the deletion function on the current node's right child.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

def b_delete(node, value, parent=None):
    if not node:
        return
    elif value < node.value:
        b_delete(node.left, value, parent=node)
    elif value > node.value:
        b_delete(node.right, value, parent=node)
    else:
        # CASE 1: remove the node from its parent
        if not node.left and not node.right:
            if parent.left and node == parent.left:
                parent.left = None
            else:
                parent.right = None

        # CASE 3: two children...
        elif node.left and node.right:
            successor = node.right
            successor_parent = node
            while successor.left:
                successor_parent = successor
                successor = successor.left
            node.value = successor.value
            b_delete(successor, successor.value, parent=successor_parent)

        # CASE 2: replace the node with its child
        else:
            if parent.left and node == parent.left:
                if node.left:
                    parent.left = node.left
                if node.right:
                    parent.left = node.right
            else:
                if node.left:
                    parent.right = node.left
                if node.right:
                    parent.right = node.right

Inserting and deleting nodes in a binary tree affects the shape of the tree, and the shape of a tree can affect the efficiency of operations on the tree. A "balanced" tree has the smallest possible height, or node depth, and is the most efficient configuration for the tree for the set of all possible searches.

In the example below, both trees contain the same data, but only one is balanced:

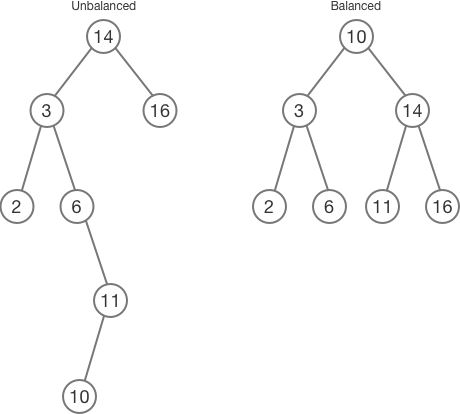
Since the efficiency of operations is inversely proportional to the height of the tree, binary trees must be periodically rebalanced to maintain efficiency. Some variations of binary trees, such as red-black trees, AVL trees, and scapegoat trees, are self-balancing, in that when a node is inserted or deleted, the tree is modified to improve its shape.