Red-Black Tree

A red-black tree is a type of binary search tree. It is self balancing like the AVL tree, though it uses different properties to maintain the invariant of being balanced. Balanced binary search trees are much more efficient at search than unbalanced binary search trees, so the complexity needed to maintain balance is often worth it. They are called red-black trees because each node in the tree is labeled as red or black.

Red-black trees maintain a slightly looser height invariant than AVL trees. Because the height of the red-black tree is slightly larger, lookup will be slower in a red-black tree. However, the looser height invariant makes insertion and deletion faster. Also, red-black trees are popular due to the relative ease of implementation.

This image shows a representation of a red-black tree. Notice how each leaf is actually a black, null value. These properties will be important in proving the tree's height invariant.

Red-Black Tree ^[1]

The red-black tree is similar to the binary search tree in that it is made up of nodes and each node has at most two children. However, there are new properties that are specific to the red-black tree.

1. Each node is either red or black, this can be saved in memory as a single bit (e.g. 'red' = 1, 'black' = 0).
2. The root of the tree is always black.
3. All leaves are null and they are black.
4. If a node is red, then its parent is black.
5. Any path from a given node to any of its descendant leaves contains the same amount of black nodes. This is sometimes known as the black-depth.
6. The height of the red-black tree is at most $2 \cdot \log_2(n + 1)$ ; this property will be proven later.

When certain nodes are inserted that upset the height invariant of the tree, the tree is then rearranged using the current coloring scheme of its nodes. Once the tree is rearranged, it is repainted to ensure that the coloring properties are maintained.

Proving the height of the red-black tree is especially important because the height of the red-black tree is what allows us to calculate it asymptotic complexity and performance. This is one method of doing so.

First imagine a red-black tree with height $h$. Now, we merge all red nodes into their black parents. A given black node can either have:

1. 2 black children, in which case the black parent still has 2 children.
2. 1 black child and 1 red child, in which case the black parent now has 3 children.
3. 2 red children, in which case the black parent now has 4 children.

Here is a graphical example of that merging process (assume any stray arrow points to a black node).

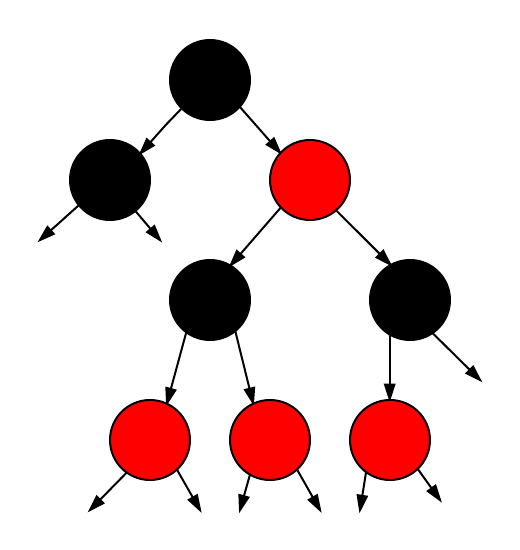Tree before the merge

Now, we merge all of the red nodes into their parent nodes. This means that any black node will now have $2 \cdot r + 2$ pointers coming out of it, where $r$ is the number of red children they have.

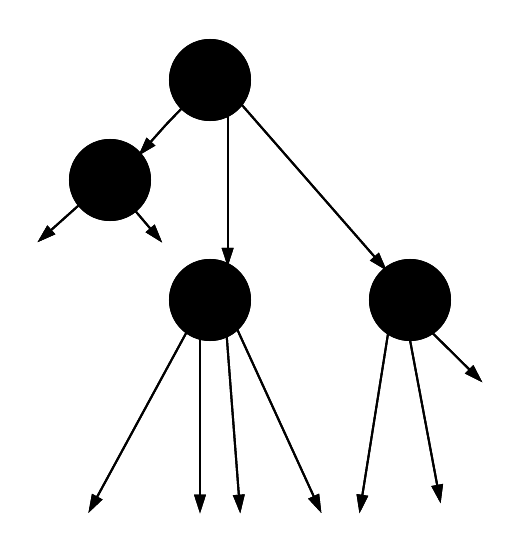Tree after the merge

As you can see, every black node has either 2, 3, or 4 children.

This new tree has a height, $h_1$. Because any given path in the original red-black tree had at most half its nodes red, we know that this new height is at least half the original height. So,

$$h_1 \ge h/2$$

The number of leaves in a tree is exactly equal to $n+1$, so

$$n+1 \ge 2^{h_1}$$ $$\log_2(n+1) \ge h_1 \ge h/2$$ $$h \le 2\log_2(n+1).$$

In a red-black tree, there are two operations that can change the structure of the tree, insert and delete. These changes might involve the addition or subtraction of nodes, the changing of a node's color, or the re-organization of nodes via a rotation. By showing the various cases and algorithms for the insertion process, though, we can infer the same things about deletion.

Inserting a node involves first searching through the tree to find its rightful spot. Then the node is inserted as a red node. This might violate the property that a red node's parent is black, though. So, now we have three potential cases that we might have to deal with.

1) Case 1

In the first case, the node we've inserted is red, its parent is red, and its parent's sibling is red. We know that the inserted node's grandparent will be black, so all we need to do is switch the coloring of the inserted node's grandparent with the coloring of the inserted node's parent and its parent's sibling. This case might need to continue to be fixed up through the root of the tree, though, because the inserted node's grandparent may have a parent who is red.

This following graphic shows this case. The node that was inserted is labeled as "INSERT". The left tree shows the case, and the right tree shows it rectified.

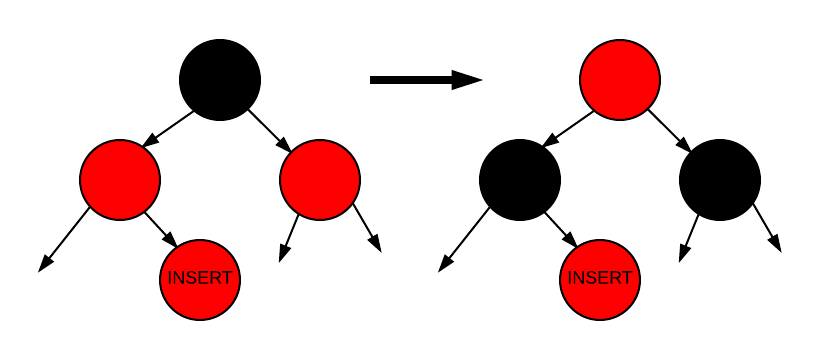Insertion - Case 1

2) Case 2

Case 2 occurs when the node's parent is red, but the parent's sibling is black, and the node's value is between those of its parent and grandparent.

We handle Case 2 by performing a rotation that takes us to Case 3. There are two kinds of rotations, a left rotation and a right rotation. Case 2 uses a left rotation because the nodes involved are rotated counter-clockwise. The following image shows the rotation in case 2. Remember, this rotation does not fully fix the problem, but it sets it up to be solved in case 3.

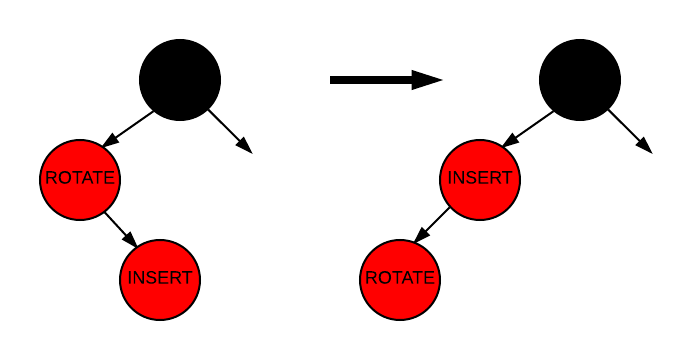Insertion - Case 2

As you can see, a left rotation was performed on the node labeled "ROTATE".

3) Case 3

Case 3 involves a right rotation on the grandparent. In the following graphic, the node to be rotated about it labeled "ROTATE", the inserted node is labeled "INSERT", and a third node "MIDDLE" has been labeled to show where it ends up after the rotation.

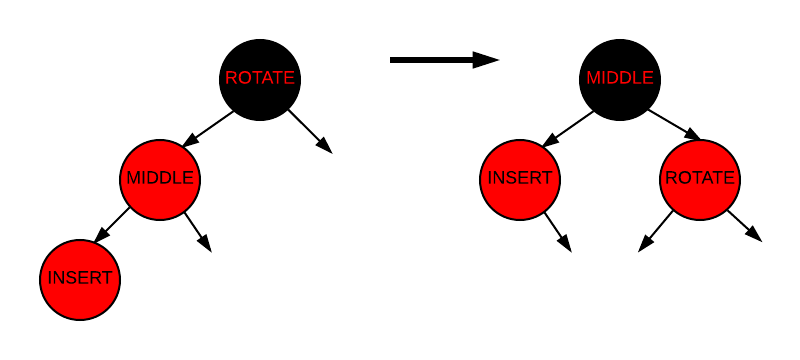Insertion - Case 3

Deletion, as stated above, works in the exact same way. Once a node has been taken out of the tree, the tree can be in any of the above 3 cases. Then the issue is resolved in the same way.

We know what needs to be done in the events of an insertion or a deletion. So what's the runtime of each operation?

As we proved earlier, the height is at most $h \le 2 \cdot \log_2(n+1)$. This means that the process of finding an index at which we can insert or delete will be an $O(\log_2(n))$ operation. At that point we can fall into any of our three cases.

In case 1, we need to back out of the tree, recoloring nodes as we go. This process also takes $O\log_2(n)$, so it doesn't increase our complexity at all.

In cases 2 and 3 we perform 1 or 2 rotations, respectively. At that point, we terminate. These cases have constant time operations. So, we know that insertion and deletion takes $O(\log_2(n))$ time.

Search in a red-black tree is the same as any balanaced binary search tree, $O\log_2(n)$ time. Traversal is a $O(n)$ amortized operation because to search through the entire tree, you simply have to enter and exit each node.

See also: big O notation.

*amortized analysis

A python implementation might look something like this. Note that this implementation is for academic purposes only and does not guarantee any functionality.

The basic node and tree class can look something like this. Each node needs to keep track of its children, its parent, its color and its key. The RBTree class will start out with nothing as its leaves and nothing as its root. Only the root will change, though.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class node:
    def __init__(self, key):
        self.key = key
        self.red = True
        self.left = None
        self.right = None
        self.parent = None

class RBTree:
    def __init__(self):
        self.root = None

A search function can be easily implemented using binary search. Note that this implementation assumes that no two keys will have the same value.

1
2
3
4
5
6
7
8

def search(self, key):
        currentNode = self.root
        while currentNode != None and key != currentNode.key:
            if key < currentNode.key:
                currentNode = currentNode.left
            else:
                currentNode = currentNode.right
        return currentNode

The insert function will behave similarly to the search in that it will find that place in the tree that the new node should go. However, it will need to call functions that will make sure the tree is fixed afterwards.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def insert(self, key):
        node = Node(key)
        #Base Case - Nothing in the tree
        if self.root == None:
            node.red = False
            self.root = node
            return
        #Search to find the node's correct place
        currentNode = self.root
        while currentNode != None:
            potentialParent = currentNode
            if node.key < currentNode.key:
                currentNode = currentNode.left
            else:
                currentNode = currentNode.right
        #Assign parents and siblings to the new node
        node.parent = potentialParent
        if node.key < node.parent.key:
            node.parent.left = node
        else:
            node.parent.right = node
        self.fixTree(node)

The fixTree method is where most of the heavy lifting takes place. It will decide what kind of case we are in and act appropriately.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

def fixTree(self, node):
        while node.parent.red == True and node != self.root:
            if node.parent == node.parent.parent.left:
                uncle = node.parent.parent.right
                if uncle.red:
                    #This is Case 1
                    node.parent.red = False
                    uncle.red = False
                    node.parent.parent.red = True
                    node = node.parent.parent
                else:
                    if node == node.parent.right:
                        #This is Case 2
                        node = node.parent
                        self.left_rotate(node)
                    #This is Case 3
                    node.parent.red = False
                    node.parent.parent.red = True
                    self.right_rotate(node.parent.parent)
            else:
                uncle = node.parent.parent.left
                if uncle.red:
                    #Case 1
                    node.parent.red = False
                    uncle.red = False
                    node.parent.parent.red = True
                    node = node.parent.parent
                else:
                    if node == node.parent.left:
                        #Case 2
                        node = node.parent
                        self.right_rotate(node)
                    #Case 3
                    node.parent.red = False
                    node.parent.parent.red = True
                    self.left_rotate(node.parent.parent)
        self.root.red = False

And here is the left_rotate method which will rotate about the given node. The right_rotate method is the exact same thing in the other direction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def left_rotate(self, node):
        sibling = node.right
        node.right = sibling.left
        #Turn sibling's left subtree into node's right subtree
        if sibling.left != None:
            sibling.left.parent = node
        sibling.parent = node.parent
        if node.parent == None:
            self.root = sibling
        else:
            if node == node.parent.left:
                node.parent.left = sibling
            else:
                node.parent.right = sibling
        sibling.left = node
        node.parent = sibling

1. burnett, C. Wikipedia Red-Black Trees. Retrieved April 25, 2016, from https://en.wikipedia.org/wiki/Red–black_tree