Braess' Paradox
Braess' Paradox states that, counterintuitively, adding a road to a road network could possibly impede its flow (e.g. the travel time of each driver); equivalently, closing roads could potentially improve travel times.
Braess' paradox, of course, has applications to traffic planning and network flow in general, but is also applicable to other fields as well. Electricity, for instance, follows many of the same principles present in network design, and so the paradox also manifests in power networks and electron systems. Surprisingly, the paradox also manifests in sports: the addition of a star player can actually reduce the efficiency of a team, essentially due to overreliance on that player.
Contents
Introduction/Intuitive explanation
If we all go for the blonde and block each other, not a single one of us is going to get her. So then we go for her friends, but they will all give us the cold shoulder because no one likes to be second choice. But what if none of us goes for the blonde? We won't get in each other's way and we won't insult the other girls. It's the only way to win. -A Beautiful Mind (2001)
In the above situation, the blonde unintentionally makes the situation worse off for everyone, as everyone "blocks each other" by acting selfishly and/or independently. Removing the blonde (or not adding her in the first place) would improve the situation for every member despite simply removing an option from consideration, an action that could (intuitively speaking) only be detrimental. This illustrates Braess' paradox, which (very roughly stated) points out that
The addition of options is not necessarily a good thing.
Intuitively speaking, this occurs when the added option is so desirable that every actor (or almost every actor) wishes to choose it, leading to a situation where the desirable option becomes so diluted that it may as well have never been there in the first place.
Example

For example, consider the road network to the right. Some of the roads only have one lane, and thus the time to travel across them depends on the number of cars \(T\) on that road. Other roads have multiple lanes, and so take 15 minutes regardless of the number of cars on it. If 4000 cars are trying to travel around this lake, there are two natural questions to ask:
- How long will it take each driver to cross the lake?
- Can the travel time be improved by adding additional roads?
The first question can be resolved by appealing to Nash equilibrium, as it is reasonable to assume that each driver will act in such a way that minimizes their expected driving time. Suppose \(A\) of the drivers choose to take the top path, and \(B\) of them choose to take the bottom path. Then the travel time along the top path is \(15 + \frac{A}{400}\), and the travel time along the bottom path is \(15 + \frac{B}{400}\). At equilibrium, these should be equal (else some drivers would choose to change their path), so \(A=B=2000\). This makes the total driving time of each driver 20 minutes.
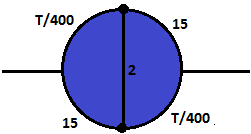
Now suppose a super-fast bridge over the lake was added, as in the network to the left. Intuitively speaking, this could only improve the situation for the drivers, as they have now gained an additional option that they could ignore if they so chose. Paradoxically, however, this actually increases the expected travel time.
The reason for this is that the bridge is so efficient that every driver would want to use it. In particular, both of the roads that take 15 minutes will never be used, as they are simply outclassed by the \(\frac{T}{400}\)-minute road combined with the 2-minute bridge (since \(T \leq 4000\)). Thus every driver would choose to take the path \(\frac{T}{400}-2-\frac{T}{400}\), making \(T=4000\), and the overall travel time \(10 + 2 + 10 = 22\) minutes.
Relation to Nash equilibrium
Because traveling can be modeled as a game in which all actors independently wish to maximize their payoff (e.g. minimize their travel time), the situation can be understood as a case of Nash equilibrium. Recall that, for any choice of payoff, at least one Nash equilibrium exists; however, it is not necessarily the case that the Nash equilibrium gives the maximum benefit possible to all actors.
For example, consider the prisoner's dilemma, in which the payoff matrix can be modeled by
| Coop. | Defect | |
| Coop. | 2,2 | 0,3 |
| Defect | 3,0 | 1,1 |
In such a game, the only Nash equilibrium occurs when both players choose to defect, but this is not a socially optimal strategy; both players cooperating would increase the benefit to both players, despite not being an equilibrium state. In other words, both players cooperating is socially optimal, or more formally Pareto efficient:
A strategy profile is Pareto efficient if no other strategy profile improves the payoff to at least one actor without decreasing the payoff of other actors.
In the Prisoner's dilemma, the profile "both players cooperate" is Pareto efficient, as no other profile increases the payoff to one player without decreasing the payoff to the other player. The Nash equilibrium state, "both players defect", is Pareto inefficient however, since the profile "both players cooperate" improves the payoff to both players.
In this sense, Braess' paradox can be rephrased as
The Nash equilibrium of a game is not necessarily Pareto efficient.
Further results
Armed with the knowledge that adding a road does not necessarily improve social cost, there are two natural follow-up questions to ask:
- When does Braess' paradox occur, and/or how often?
- When Braess' paradox does occur, how badly does it affect the social cost?
Interestingly, the answers to these questions are counterintuitive as well. Intuition would suggest that Braess' paradox is relatively rare, as it seems to only hold under very specific conditions, and it would also suggest that the addition of a road could heavily impact the social situation.
However, it can be shown that
In a random network, the addition of an edge causes Braess' paradox with probability roughly \(\frac{1}{2}\)
which is surprisingly high. It can also be shown that
If the travel time for each road is linear in the traffic flow across them, adding an edge cannot make the total travel time worse by more than a factor of \(\frac{4}{3}\).
which is a somewhat surprising (and comforting) upper bound, since travel time across a road does tend to be roughly linear in practice.