Complex Numbers

A complex number is a number that can be written in the form $a + bi$, where $a$ and $b$ are real numbers and $i$ is the imaginary unit defined by $i^2 = -1$. The set of complex numbers, denoted by $\mathbb{C}$, includes the set of real numbers $\left( \mathbb{R} \right)$ and the set of pure imaginary numbers.

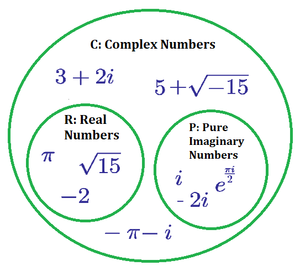Venn Diagram of Complex Numbers

Bombelli's L'Algebra (1572) contained the first major treatise on complex numbers. Prior to this book, Cardano's method could be used to find the roots of a cubic equation, but it would occasionally require taking the square root of a negative number as an intermediary step, even if the end result was a real number. Bombelli outlined the arithmetic behind these complex numbers so that these real roots could be obtained.

When talking about complex numbers, the term "imaginary" is somewhat of a misnomer. The original intent in calling numbers "imaginary" was derogatory as if to imply that the numbers had no worth in the real world. On the contrary, complex numbers are now understood to be useful for many practical problems involving real-world things. Their relationship to trigonometry and polar coordinates makes them particularly useful for physics and engineering applications.

Based on the nature of the real part and imaginary part, any complex number can be classified into four types:

• imaginary number
• zero complex number
• purely imaginary number
• purely real number.

For $Z = a + ib,$ the following four cases arise:

$$\begin{array}{lll} a \neq 0 \qquad b \neq 0 \qquad \implies a + ib && : \qquad \text{imaginary number} \\ a = 0 \qquad b = 0 \qquad \implies 0 + i0 && : \qquad \text{zero complex number} \\ a = 0 \qquad b \neq 0 \qquad \implies ib && : \qquad \text{purely imaginary number} \\ a \neq 0 \qquad b = 0 \qquad \implies a && : \qquad \text{purely real number}. \end{array}$$

One thing you have to remember is the following:

Every real number is a complex number, but every complex number is not necessarily a real number.

The set of all complex numbers is denoted by $Z \in \mathbb C$. The set of all imaginary numbers is denoted as $Z \in \mathbb C - \mathbb R$.

Main Article: Complex Plane

Complex numbers are often represented on the complex plane, sometimes known as the Argand plane or Argand diagram. In the complex plane, there are a real axis and a perpendicular, imaginary axis. The complex number $a+bi$ is graphed on this plane just as the ordered pair $(a,b)$ would be graphed on the Cartesian coordinate plane. The real axis corresponds to the $x$-axis and the imaginary axis corresponds to the $y$-axis.

Complex Numbers Graphed in the Complex Plane

The main advantage that complex numbers have over ordered pairs is that the operations of addition and multiplication are defined for complex numbers, whereas these operations are not defined for ordered pairs.

In a complex number $Z = a + ib,$

$$Z = \underbrace{a}_{\overset{\text{real}}{\text{part}}} + \underbrace{i}_{\overset{\text{imaginary}}{\text{unit}}} \underbrace{b}_{\overset{\text{imaginary}}{\text{part}}}.$$

Here, $i$ is called the imaginary unit and, mathematically, its value is $i = \sqrt{-1}.$

In this section, we will discuss some important properties of $i:$

• $i = \sqrt{-1}$
• $i^2 = \big(\sqrt{-1}\big)^2 = -1$
• $i^3 = i \cdot i^2 = i \cdot (-1) = -i$
• $i^4 = i^2 \cdot i^2 = (-1) \cdot (-1) = 1.$

To simplify larger powers of $i$, take the last two digits of the number and divide it by $4$. Find the remainder and if the remainder is $k,$ then the value is $i^k.$

Simplify $i^{2018},$ where $i = \sqrt{-1}.$

---

The given expression is $i^{20\color{#3D99F6}18}$. Collect the last two digits of the power; here it is $\color{#3D99F6}18$.

Now, on dividing $18$ by $4,$ we get the remainder as $2$.

Therefore, $i^{2018} = i^2 = -1.\ _\square$

The value of

$$i^k + i^{k + 1} + i^{k + 2} + i^{k + 3} = 0,$$

where $k$ is an integer.

This can also be said, "the sum of four consecutive powers of $i$ is equal to 0."

Find the value of $i + i^2 + i^3 + i^4$.

---

From the above result, we can directly say that the value is $0$ as it is the sum of 4 consecutive powers of $i.$

Or, you can also find this as follows:

$$i + i^2 + i^3 + i^4 = i - 1 - i + 1 = 0.\ _\square$$

Find the value of $\displaystyle \sum_{k = 1} ^{200} i^k.$

---

We can write the given expression as

$$\big(1^1 + 1^2 + i^3 + i^4\big) + \big(i^5 + i^6 + i^7 + i^8\big) + \cdots + \big(i^{193} + i^{194} + i^{195} + i^{196}\big) + \big(i^{197} + i^{198} + i^{199} + i^{200}\big).$$

Now, from the above result, the value in every bracket becomes $0$ as the sum of 4 consecutive powers $i$ equal to $0$. There are 50 brackets and every bracket equals to 0.

Therefore, $50(0) =0.\ _\square$

Adding complex numbers follows the algebraic principle of combining like terms. The real parts of complex numbers are considered to be alike and, likewise, the complex parts are considered to be alike.

Addition of Complex Numbers:

Given complex numbers $a + bi$ and $c+di$, their sum is

$$(a+c) + (b+d)i.$$

What is $(4+3i)+(2+2i)?$

---

Adding the real and imaginary parts separately, we get

$$4+3i+2+2i = (4+2) + (3+2)i = 6+5i.\ _\square$$

Notice how real numbers were only added to other real numbers and imaginary numbers were only added to other imaginary numbers.

A few additional examples:

• $(3-4i)+(3+2i) = 6-2i$
• $(4-2i)-(-2-5i) = 6+3i$
• $(3i)+(3+5i) = 3+8i$

Multiplying complex numbers follows the principle of multiplying binomials. One notable difference is that when the imaginary terms are multiplied, it produces a real number.

Multiplication of Complex Numbers:

Given two complex numbers $a + bi$ and $c+di$, their product is

$$\begin{aligned} (a+bi) \times (c+di) &= a(c+di) + bi(c+di) \\ &= (ac) + (ad)i + (bc)i + (bd)i^2 \\ &= (ac) + (ad+bc)i + (bd)(-1) \\ &= (ac - bd) + (ad+bc)i . \end{aligned}$$

Note: It is better recommended not to remember the above formula, as multiplication of two complex numbers can be done just like normal multiplication of two real expressions.

What is $(3+2i)(4-2i)?$

---

Solution 1:
By the definition above, $a=3, b=2, c=4, d=-2$, so the product is

$$\big(12 - (-4)\big) + (-6+8)i = 16 + 2i.\ _\square$$

Solution 2:
Working out the product from first principles, we have

$$\begin{aligned} (3+2i)(4-2i) &= 3(4-2i)+2i(4-2i) \\ &= 12-6i + 8i -4i^2 \\ &= 16 +2i.\ _\square \end{aligned}$$

If $x = 1+2i$, what is the value of $x^3 + 2x^2 + 4x + 25?$

---

Solution 1:
We could evaluate each of the terms individually and then add:

• $x^3 = (1+2i)^3 = -11 - 2i$
• $2x^2 = 2(1+2i)^2 = 2(-3+4i) = -6+8i$
• $4x = 4(1+2i) = 4 + 8i .$

Therefore, $x^3 + 2x^2 + 4x + 25 = (-11 - 2i)+( -6+8i) + (4 +8i) + 25 = 12+14i$. $_\square$

Solution 2:
Since $x = 1 +2i$, $x-1 = 2i$. Squaring both sides gives

$$x^2 -2x +1=4i^2 \implies x^2-2x +5 = 0. \qquad (1)$$

Then

$$\begin{aligned} x^3 + 2x^2 + 4x +25 &= \big(x^2-2x+5\big)\left(x+4\right) + 7x + 5 \\ &= 0 \cdot (x+4) + 7x +5 \qquad \qquad \qquad \big(\text{by }(1)\big) \\ &= 7(1+2i) + 5 \\ &= 12 + 14i. \ _\square \end{aligned}$$

Division of Complex Numbers:

If $Z_1 = a + ib$ and $Z_2 = c + id$ are any two complex numbers, the division of the two complex numbers is done by just rationalizing the complex number or multiplying and dividing by the conjugate of the denominator.

This is discussed in the below section.

Main Article: Complex Conjugates

The complex conjugate of a complex number $a+bi$ is $a-bi$.

Name the complex conjugates of the following numbers:

• $-5+6i$

• $\frac{8}{3}-i$

• $-2i$

• $17.$

---

Their complex conjugates are as follows:

• $-5+6i \implies -5-6i$

• $\frac{8}{3}-i \implies \frac{8}{3}+i$

• $-2i \implies 2i:$ the complex conjugate of an imaginary number is the negation of that number.

• $17 \implies 17:$ the complex conjugate of a real number is the number itself. $_\square$

A complex conjugate can also be thought of as the reflection of a complex number about the real axis in the complex plane.

Complex Conjugate Pairs in the Complex Plane

Complex conjugates are useful for rationalizing denominators that contain complex numbers. The process of rationalizing a complex denominator is very similar to how the process works for radicals.

Rationalize the denominator and write in standard form:

$$\frac{3+2i}{5-2i}.$$

---

The conjugate of the denominator is $5+2i.$ Multiply both the numerator and denominator by this number:

$$\begin{aligned} \frac{3+2i}{5-2i} &= \frac{(3+2i)(5+2i)}{(5-2i)(5+2i)} \\ \\ &= \frac{11+16i}{29} \\ \\ &= \frac{11}{29}+\frac{16}{29}i.\ _\square \end{aligned}$$

In addition, the complex conjugate root theorem states how complex roots of polynomials always come in conjugate pairs.

Complex Conjugate Root Theorem:

If $a+bi$ is a root of a polynomial with rational coefficients, then $a-bi$ is also a root of that polynomial.

The following quadratic has $1+i$ as a root:

$$x^2+bx+c.$$

If $b$ and $c$ are integers, then what is $b+c?$

---

Given that $b$ and $c$ are integers, the other root must be the conjugate of $1+i.$ Writing the polynomial in factored form gives

$$\begin{aligned} x^2+bx+c &= (x-1-i)(x-1+i) \\ &= x^2-2x+2, \end{aligned}$$

which implies $b=-2$ and $c=2,$ so $b+c=0.$ $_\square$

If $\left|z_1\right|=\left|z_2\right|=\left|z_3\right|=\ldots=\left|z_n\right|=1,$ then prove that

$$\left|\frac{1}{z_1}+\frac{1}{z_2}+\frac{1}{z_3}+\cdots+\frac{1}{z_n}\right|=\left|z_1+z_2+z_3+\cdots+z_n\right|.$$

---

We have

$$\begin{aligned} \left|z_1\right|=\left|z_2\right|=\left|z_3\right|=\ldots=\left|z_n\right|&=1 \\\\ \left|z_1\right|^2=\left|z_2\right|^2=\left|z_3\right|^2=\ldots=\left|z_n\right|^2&=1 \\\\ z_1\overline{z_1}=1, z_2\overline{z_2}=1, z_3\overline{z_3}=1, \ldots, z_n\overline{z_n}&=1\\\\ \frac{1}{z_1}=\overline{z_1}, \frac{1}{z_2}=\overline{z_2}, \frac{1}{z_3}=\overline{z_3}, \ldots, \frac{1}{z_n}&=\overline{z_n}\\\\ \left| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|\overline{z_1}+ \overline{z_2}+ \overline{z_3}+ \cdots+\overline{z_n}\right|\\\\ &=\left|\overline{z_1+ z_2+z_3+ \cdots+z_n}\right|\\\\ &=\left|z_1+ z_2+z_3+ \cdots+z_n\right| \qquad \big(\text{since } \left|\overline{z}\right|=\left|z\right|\big)\\\\ \Rightarrow \left| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|z_1+ z_2+z_3+ \cdots+z_n\right|.\ _\square \end{aligned}$$

Main Article: Gaussian Integers

A Gaussian integer is a complex number $a+bi,$ where both $a$ and $b$ are integers. It should be noted that a Gaussian integer is not actually an integer unless the imaginary part is equal to 0.

Gaussian integers:

• $3+2i$

• $7-8i$

• $14$

• $-92i$

Non-Gaussian integers:

• $\frac{1}{2}+\frac{\sqrt{3}}{2}i$

• $7-\frac{i}{3}$

Gaussian integers are of interest in number theory because the problems of quadratic, cubic, and quartic reciprocity are more conveniently stated as problems about Gaussian integers.

Main Article: Complex Numbers - Absolute Values

See Also: Converting Cartesian Coordinates to Polar

It should be noted that the process to find the modulus and argument of a complex number is nearly identical to the process of converting Cartesian coordinates to polar coordinates.

The absolute value of a real number is defined as the positive distance from 0 to that number. The absolute value of a complex number is defined in the same way, except this distance is measured on the complex plane.

Since the segment connecting 0 with the complex number is a hypotenuse of a right triangle, the distance of this segment is computed with the Pythagorean theorem. This distance is sometimes called the modulus of the complex number.

The modulus of a complex number $a+bi$ is

$$|a+bi|=\sqrt{a^2+b^2}.$$

Compute $|3-4i|.$

---

We have

$$|-3+4i|=\sqrt{(-3)^2+4^2}=5.\ _\square$$

The angle that the positive real axis makes with the ray that connects $0$ with a complex number is called the argument of that complex number.

Just like the modulus, the argument of a complex can be computed using triangle relationships.

The argument of a complex number $a+bi$ is the angle, $\theta$, defined by the equation

$$\tan{\theta}=\frac{b}{a}.$$

$\theta$ can be solved for by taking the inverse tangent of the above equation, but one must take care to account for the quadrant that the complex number is located in.

Compute the argument of $-3+4i.$

---

We have

$$\tan{\theta}=-\frac{4}{3}.$$

Recall that the inverse tangent function has a range of $\left(-\frac{\pi}{2},\frac{\pi}{2}\right).$ Taking the inverse tangent will give the angle that is in the $4^\text{th}$ quadrant. This number is in the $2^\text{nd}$ quadrant, so $\pi$ should be added to this angle to give the correct argument:

$$\theta=\tan^{-1}\left(-\frac{4}{3}\right)+\pi.\ _\square$$

A full rotation of a complex number of $2\pi$ radians will produce an image that is co-terminal with the complex number. Therefore, each complex number has infinitely many arguments.

If $\theta$ is the argument of a complex number, then $\theta+2k\pi$ is also an argument of that complex number, where $k$ is an integer.

Main Article: Fundamental Theorem of Algebra

See Also: Quadratic Formula and Discriminant of a Quadratic

By the fundamental theorem of algebra, every polynomial of degree $n$ has exactly $n$ roots, counting for multiplicity. However, sometimes these roots are complex numbers rather than real numbers. As a simple example, $x^2 +1 = 0$ is only true when $x^2 = -1$, which of course is only possible if $x =\pm i$.

Find the roots of the equation $2x^2 + 1 = 0.$

---

Subtracting $1$ and then halving both sides, we get $x^2 = \frac{-1}{2}.$ Thus,

$$\begin{aligned} x &= \pm \sqrt \frac{-1}{2}\\ &=\pm \sqrt{-1} \sqrt\frac{1}{2}\\ &=\pm i \sqrt{\frac{1}{2}}\\ &=\pm \frac{i}{\sqrt{2}} .\ _\square \end{aligned}$$

Factor the following quadratic: $x^2 + 6x + 10.$

---

Computing the discriminant $D$, we get

$$D = b^2 - 4ac = 6^2 - 4\times1\times10 = -4 .$$

It is less than $0$ and thus we can conclude that the quadratic has a pair of complex roots with imaginary components. To find them, we use the quadratic formula as follows:

$$\begin{aligned} x &= \frac{ -b \pm \sqrt{D}}{2a} \\ & = \frac{-6 \pm \sqrt{-4}}{ 2 \times 1} \\ & = \frac{ -6 \pm 2\sqrt{-1}}{2} \\ &=-3 \pm i . \end{aligned}$$

Factorizing the expression, we get

$$\begin{aligned} x^2+6x+10 &=\big(x-(-3+i)\big)\big(x-(-3-i)\big)\\ &=(x+3-i)(x+3+i). \ _\square \end{aligned}$$

Find the roots of $3x^2 + 5ix + 7 = 0.$

---

Computing the discriminant $D$, we get

$$D = b^2 - 4ac = (5i)^2 - 4\times3\times7 = -109.$$

It is indeed less $0$ and thus we can conclude that the quadratic has a pair of complex roots. To find them, we use the quadratic formula as follows:

$$\begin{aligned} x &= \frac{ -b \pm \sqrt{D}}{2a} \\ &= \frac{-5i \pm \sqrt{-109}}{ 2 \times 3} \\ &= \frac{ -5i \pm \sqrt{109} \sqrt{-1}}{6}. \end{aligned}$$

Thus, the roots are

$$\begin{array}{c}&x =\left (\frac{-5-\sqrt{109}}{6}\right)i &\text{and} &x = \left(\frac{-5+\sqrt{109}}{6}\right)i .\end{array} \ _\square$$

Main Article: Euler's Formula

See Also: De Moivre's Theorem

The form $a+bi$ is known as the standard form of a complex number. Euler's formula gives a way to express a complex number in exponential form.

Euler's Formula:

Given a complex number $z$ with modulus $r$ and argument $\theta,$

$$z=re^{i\theta}=r\left(\cos{\theta}+i\sin{\theta}\right).$$

Express $3e^{\pi i/2}$ in standard form.

---

We have

$$\begin{aligned} 3e^{\pi i/2} &= 3\left(\cos \frac{\pi}{2}+i\sin\frac{\pi}{2}\right) \\ &= 3i.\ _\square \end{aligned}$$

Express $\frac{1}{2}-i\frac{\sqrt{3}}{2}$ in exponential form.

---

Compute the modulus:

$$\begin{aligned} \left|\frac{1}{2}-i\frac{\sqrt{3}}{2}\right| &= \left(\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2 \\ \\ &=1. \end{aligned}$$

Compute the argument:

$$\begin{aligned} \tan{\theta} &= -\sqrt{3} \qquad \big(\text{number is in the } 4^\text{th} \text{ quadrant}\big) \\ \theta &= -\frac{\pi}{3}. \end{aligned}$$

With the modulus and argument, the exponential form follows directly:

$$\frac{1}{2}-i\frac{\sqrt{3}}{2}=e^{-\pi i/3}.\ _\square$$

Euler's Identity is a special case of Euler's formula in which $r=1$ and $\theta=\pi.$ It is notable because it incorporates several important mathematical constants $(0, 1, \pi, e,$ and $i)$ all in one equation.

Euler's Identity:

$$e^{\pi i}+1=0$$

De Moivre's theorem gives a way to raise a complex number to any real number power. It follows directly from Euler's formula.

De Moivre's Theorem:

Given a complex number $z=re^{i\theta}$ and a real number $n,$

$$z^n=\big(re^{i\theta}\big)^n=r^n\big[\cos(n\theta)+i\sin(n\theta)\big].$$

Compute $\big(\sqrt{2}+i\sqrt{2}\big)^4$ in standard form.

---

Compute the modulus of the base complex number:

$$\begin{aligned} \big|\sqrt{2}+i\sqrt{2}\big| &= \sqrt{(\sqrt{2})^2+(\sqrt{2})^2} =2 . \end{aligned}$$

Compute the argument of the base complex number:

$$\begin{aligned} \tan{\theta} &=1 \qquad \big(\text{number is in the } 1^\text{st}\text{ quadrant}\big) \\ \theta &= \frac{\pi}{4}. \end{aligned}$$

Convert to exponential form and apply De Moivre's theorem:

$$\begin{aligned} \big( \sqrt{2}+i\sqrt{2} \big)^4 &= \big(2e^{\pi i/4}\big)^4 \\ &= 2^4\left(\cos{\pi}+i\sin{\pi}\right) \\ &= -16.\ _\square \end{aligned}$$

Main Article: Roots of Unity

The $n^\text{th}$ roots of unity are the complex solutions to an equation of the form $x^n=1,$ where $n$ is a positive integer. They can be solved for by applying Euler's formula and De Moivre's theorem.

What are the complex solutions to the equation $x^6=1?$

---

We have

$$\begin{aligned} 1&=e^{2k\pi i},\ k \in \mathbb{Z}\\ x^6&=e^{2k\pi i}\\ x&=e^{k\pi i/3}. \end{aligned}$$

Below are $6$ values of $k$ that give distinct complex numbers. All other values of $k$ give arguments that are co-terminal with these complex numbers:

$$\begin{array}{lll} k=0: & x=e^0 & = 1 \\ k=1: & x=e^{\pi i/3} & = \frac{1}{2}+i\frac{\sqrt{3}}{2} \\ k=2: & x=e^{2\pi i/3} & = -\frac{1}{2}+i\frac{\sqrt{3}}{2} \\ k=3: & x=e^{\pi} & = -1 \\ k=4: & x=e^{4\pi i/3} & = -\frac{1}{2}-i\frac{\sqrt{3}}{2} \\ k=5: & x=e^{5\pi i/3} & = \frac{1}{2}-i\frac{\sqrt{3}}{2}. \end{array}$$

These solutions are called the $6^\text{th}$ roots of unity. $_\square$

Main Article: Complex Numbers in Geometry

Because of the circular relationships associated with complex numbers, they are useful for many geometry problems. For example, the rotation of a point or rigid figure can be performed with complex numbers much more simply than it can be done with trigonometry.

To rotate a point $\theta$ radians counterclockwise about the origin,

• first convert the ordered pair to the corresponding complex number;
• multiply this complex number by $e^{i\theta}$;
• convert this result to the corresponding ordered pair.

To rotate a rigid figure $\theta$ radians counterclockwise about the origin, rotate each point in the figure following the process above.

The point $(2,5)$ is rotated $30^\circ$ counterclockwise about the origin. What is the image of rotation?

---

The corresponding complex number is $2+5i.$ The angle of rotation is $\frac{\pi}{6}.$ This gives the complex number

$$e^{\pi i/6}=\frac{\sqrt{3}}{2}+\frac{i}{2}.$$

Multiply these complex numbers to obtain the image of rotation:

$$\left(2+5i \vphantom{\frac{\sqrt{3}}{2}}\right)\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)=\sqrt{3}-\frac{5}{2}+i\left(1+\frac{5\sqrt{3}}{2}\right).$$

The corresponding ordered pair is $\left(\sqrt{3}-\frac{5}{2},\ 1+\frac{5\sqrt{3}}{2}\right).$ $_\square$

There are several other applications of complex numbers in geometry in the wiki page on this topic.