Trigonometry
Trigonometry concerns the description of angles and their related sides, particularly in triangles. While of great use in both Euclidean and analytic geometry, the domain of the trigonometric functions can also be extended to all real and complex numbers, where they become useful in differential equations and complex analysis.
Contents
Elementary Definition and Usage
Consider the familiar example of a 45-45-90 right triangle, whose angles are \( 45^\circ, \) \( 45^\circ, \) and \( 90^\circ. \) By the Pythagorean theorem, such a triangle must have a hypotenuse whose length is \( \sqrt{2} \) times that of each of the legs:
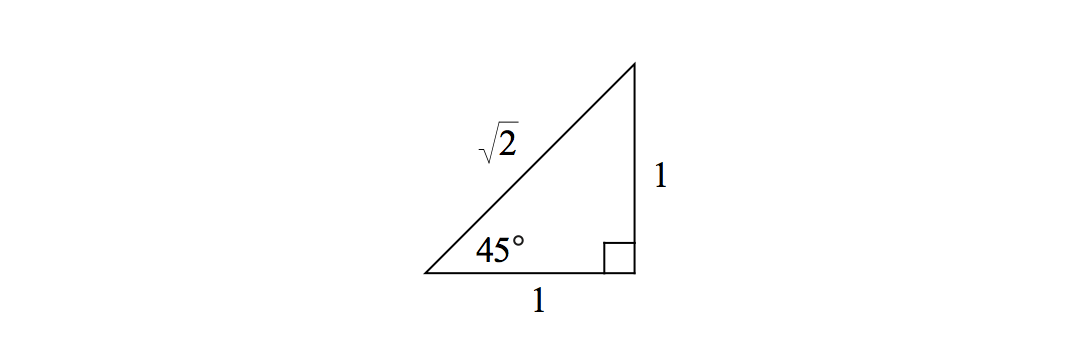
In this case, relative to one of the acute angles of the triangle, one can write the ratio of the sides as
\[ \frac{\text{opposite side}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}}, \quad \frac{\text{adjacent side}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}}, \quad \frac{\text{opposite side}}{\text{adjacent side}} = 1. \]
In a 30-60-90 right triangle, whose angles are \( 30^\circ, \) \( 60^\circ, \) and \( 90^\circ, \) the longer leg has length \( \sqrt{3} \) times that of the shorter leg while the hypotenuse has length twice that of the shorter leg:
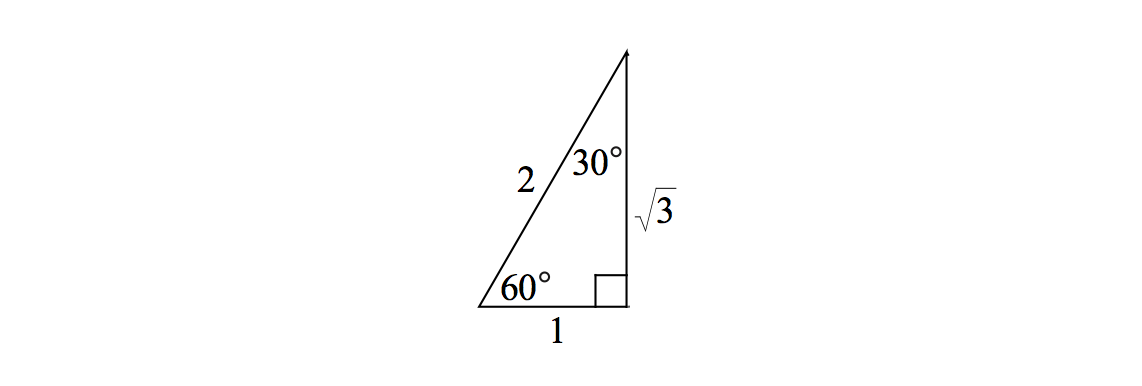
In this case, relative to the \( 30^\circ \) angle, one can write the ratio of the sides as
\[ \frac{\text{opposite side}}{\text{hypotenuse}} = \frac{1}{2}, \quad \frac{\text{adjacent side}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}, \quad \frac{\text{opposite side}}{\text{adjacent side}} = \frac{1}{\sqrt{3}}. \]
In both cases, specifying the acute angles of the right triangle determines the relative ratios between each of the sides. As one angle grows smaller and the other grows larger, the side opposite the larger angle grows larger while the side opposite the smaller angle grows smaller.
There is no reason that the ratios cannot be specified for any arbitrary right triangle. In principle, given one of the acute angles of a right triangle, the ratios between each pair of sides is fixed. In other words, the ratios between the sides can be considered functions of the measure of an acute angle. In trigonometry, the three ratios form the basis of definition of the three basic trigonometric functions, called the sine, cosine, and tangent.
Given an acute angle \( \theta \), construct a right triangle one (or both) of whose acute angles is \( \theta \):
The sine of \( \theta \) is written as \( \sin{\theta} \) and defined as the ratio \[ \sin{\theta} = \frac{\text{opposite side}}{\text{hypotenuse}}. \]
The cosine of \( \theta \) is written as \( \cos{\theta} \) and defined as the ratio \[ \cos{\theta} = \frac{\text{adjacent side}}{\text{hypotenuse}}. \]
The tangent of \( \theta \) is written as \( \tan{\theta} \) and defined as the ratio \[ \tan{\theta} = \frac{\text{opposite side}}{\text{adjacent side}} = \frac{\sin{\theta}}{\cos{\theta}}. \]
It is worth noting that as \( \theta \) goes from \( 0^\circ \) to \( 90^\circ \), the sine goes from \( 0 \) to \( 1 \) while the cosine goes from \( 1 \) to \( 0 \). Meanwhile, the tangent goes from \( 0 \) to \( \infty \).
Additionally, since they are frequently used, the reciprocals of sine, cosine, and tangent also have names: they are the cosecant, secant, and cotangent.
The cosecant of \( \theta \) is written as \( \csc{\theta} \) and defined as \[ \csc{\theta} = \frac{1}{\sin{\theta}}. \]
The secant of \( \theta \) is written as \( \sec{\theta} \) and defined as \[ \sec{\theta} = \frac{1}{\cos{\theta}}. \]
The cotangent of \( \theta \) is written as \( \cot{\theta} \) and defined as \[ \cot{\theta} = \frac{1}{\tan{\theta}}. \]
While the values of the trigonometric functions for certain angles may be computed to be an algebraic number (i.e., expressible in terms of fractions and roots alone), in general the sine or cosine of an arbitrary angle may be transcendental. This is proven by Baker's theorem.
Compute the value of the six trigonometric functions for \( \theta = 30^\circ \).
From what we know about the 30-60-90 right triangle, we have
\[ \sin{30^\circ} = \frac{\text{opposite side}}{\text{hypotenuse}} = \frac{1}{2}, \quad \cos{30^\circ} = \frac{\text{adjacent side}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}, \quad \tan{30^\circ} = \frac{\text{opposite side}}{\text{adjacent side}} = \frac{1}{\sqrt{3}}. \]
Thus
\[ \csc{30^\circ} = \frac{1}{\sin{30^\circ}} = 2, \quad \sec{30^\circ} = \frac{1}{\cos{30^\circ}} = \frac{2}{\sqrt{3}}, \quad \cot{30^\circ} = \frac{1}{\tan{30^\circ}} = \sqrt{3}.\ _\square\]
Recall that two angles and the side between them or two sides and the angle between them specify a unique triangle. Ultimately, the trigonometric functions allow one to specify all of the unknown sides and angles for a uniquely determined triangle.
A right triangle has a hypotenuse of length \( L \). If the smaller of the two angles in the triangle is \( \theta \), what are the lengths of the two legs of the right triangle?
The length of the shorter side (the side opposite \( \theta \) must be equal to \( L \sin{\theta} \) from the definition of the sine. It follows that the length of the longer side, which is the side adjacent to \( \theta \), must be \( L \cos{\theta} \). \(_\square\)
The Unit Circle
To extend the domain of the trigonometric functions to all angles, not just those that exist as the acute angle of a right triangle, one can consider the coordinates of a point located on a unit circle. Drawing the radius of the circle to a point on the circle gives a right triangle whose hypotenuse is of unit length and whose legs lie entirely on the coordinate axes. In this way, one can define the trigonometric functions in terms of the \( x \)- and \( y \)-coordinates of a point on the unit circle. The angle is specified by the angle of the radius drawn as measured from the positive \( x \)-axis. This allows the trigonometric functions to be defined for any angle, even those greater than \( 360^\circ \) (representing a rotation that goes around more than once) or less than \( 0^\circ \) (representing a clockwise rotation).

Given an angle \( \theta \), let \( x \) and \( y \) be the coordinates of the point on the unit circle such that the angle formed between the radius and the positive \( x \)-axis is \( \theta \). Then
\[ \sin{\theta} = y, \quad \cos{\theta} = x, \quad \tan{\theta} = \frac{y}{x}.\]
With the extended definition, the trigonometric functions can take on negative values:
- In the first quadrant (\( +x \) axis and \( +y \) axis), sine and cosine are both positive.
- In the second quadrant (\( - x \) axis and \( +y \) axis), sine is positive while cosine is negative.
- In the third quadrant (\( -x \) axis and \( - y \) axis), sine and cosine are both negative.
- In the fourth quadrant (\( +x \) axis and \( -y \) axis), sine is negative while cosine is positive.
Cosine goes from \( 1 \) to \( 0 \) to \( -1 \) to \( 0\) and finally back to \( 1 \), while sine does the opposite: first from \( 0 \) to \( 1 \) and then to \( 0 \) followed by \( -1 \) and then back to \( 0 \). One full period requires \( 360^\circ \), or \( 2 \pi \) by radian angle measure, with both graphs staggered by \( 90^\circ. \)

Properties of the Trigonometric Functions
The trigonometric functions have several interesting analytic properties. First, as mentioned, sine and cosine both have a period of \( 2 \pi: \)
\[\begin{align} \sin{\theta} &= \sin(\theta + 2 \pi) \\ \cos{\theta} &= \cos(\theta + 2 \pi) \end{align}\]
Tangent, meanwhile, has a period of only \( \pi \) since the relative sign of sine compared to cosine only requires a period of \( \pi \) to make a full cycle (flipping from positive to negative and back to positive):
\[ \tan{\theta} = \tan(\theta + \pi) \]
As is apparent from the graph, cosine is even while sine is odd:
\[ \begin{align} \sin(-\theta) &= -\sin{\theta} \\ \cos(-\theta) &= \cos{\theta} \end{align} \]
A property that connects sine together with cosine is the fact that sine is simply cosine staggered by shift of \( \frac{\pi}2. \) Clearly, this must be true because the sine of an angle must be equal to the cosine of its complement; the opposite side of one angle in a right triangle is the adjacent side of the complementary angle:
\[ \sin{\theta} = \cos\left(\theta - \frac{\pi}2\right) \]
Those familiar with calculus will know that the derivatives of sine and cosine are closely related:
For \( \theta \) measured in radians,
\[ \frac{d}{d\theta} \sin{\theta} = \cos{\theta}, \quad \frac{d}{d\theta} \cos{\theta} = -\sin{\theta}. \]
Similar properties apply for the other trigonometric functions.
Trigonometric Identities
In practice, expressions containing trigonometric functions can get quite complicated. One means to simplify them is to utilize various identities. Among the most famous of these are the sum and difference formulas. These identities allow one to expand a trigonometric function whose argument is the sum or difference of two angles. These identities can be proven using fairly straightforward geometric arguments, among other methods.
Sum and Difference formulas:
\[ \begin{align} \sin(\alpha \pm \beta) &= \sin{\alpha} \cos{\beta} \pm \cos{\alpha} \sin{\beta} \\\\ \cos(\alpha \pm \beta) &= \cos{\alpha} \cos{\beta} \mp \sin{\alpha} \sin{\beta} \end{align} \]
What is \( \cos{105^\circ}? \)
Using the sum formula for cosine, we can express \( \cos{105^\circ} \) as
\[ \begin{align} \cos{105^\circ} &= \cos(60^\circ + 45^\circ) \\ &= \cos{60^\circ} \cdot \cos{45^\circ} - \sin{60^\circ} \cdot \sin{45^\circ} \\ &= \frac{1}{2} \cdot \frac{\sqrt{2}}{2} - \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{2}}{4} - \frac{\sqrt{6}}{4} \\ &= \frac{\sqrt{2}-\sqrt{6}}{4} . \ _\square \end{align} \]
Simplify \( \cos{140^\circ} \cdot \cos{50^\circ} + \sin{140^\circ} \cdot \sin{50^\circ}. \)
Using the difference formula for cosine, we can write
\[ \cos{140^\circ} \cdot \cos{50^\circ} + \sin{140^\circ} \cdot \sin{50^\circ} = \cos(140^\circ - 50^\circ) = \cos 90^\circ = 0. \]
The Pythagorean identities follow as a consequence of the Pythagorean theorem. If \( a \) and \( b \) are the lengths of the legs of a right triangle with \( c \) the length of the hypotenuse, then \( a^2 + b^2 = c^2 \) implies
\[ \left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 = 1, \]
so
\[ \sin^2{\theta} + \cos^2{\theta} = 1. \]
\(\big(\)By convention, one usually writes \( \sin^2{\theta} \) to indicate the square \( (\sin{\theta})^2 \) and not the composition of functions \( \sin(\sin{\theta}).\big) \)
One my also divide by \( \sin^2{\theta} \) or \( \cos^2{\theta} \) to obtain different forms of the identity.
Pythagorean Identities:
\[ \begin{align} \sin^2{\theta} + \cos^2{\theta} &= 1 \\\\ 1 + \cot^2{\theta} &= \csc^2{\theta} \\\\ \tan^2{\theta} + 1 &= \sec^2{\theta} \end{align} \]
From these basic identities and properties, a whole host of other trigonometric identities can be proven.
Law of Sines and Law of Cosines
Two theorems regarding sine and cosine in triangles are particularly worth noting. The law of sines relates the side lengths of a triangle (not necessarily just a right triangle) to their opposite angles, while the law of cosines generalizes the Pythagorean theorem.
Law of Sines
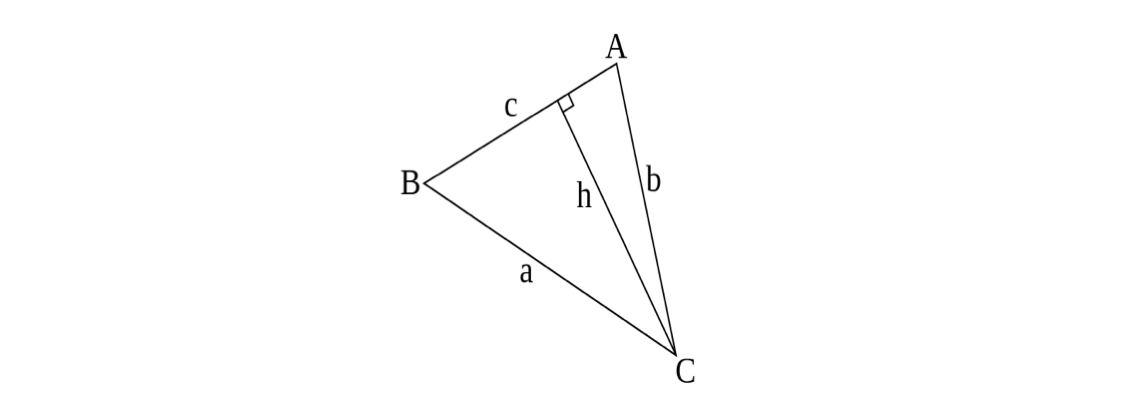
Let \( A, B, C \) denote the measures of the angles at the corresponding vertices, and let \( a, b, c \) denote the side lengths of the opposite sides of the respective angles.
It holds that
\[ \frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}}. \]
Law of Cosines

Let \( A, B, C \) denote the measures of the angles at the corresponding vertices, and let \( a, b, c \) denote the side lengths of the opposite sides of the respective angles.
It holds that
\[ \begin{align} a^2 &= b^2 + c^2 - 2bc \cos{A} \\ b^2 &= a^2 + c^2 - 2ac \cos{B} \\ c^2 &= a^2 + b^2 - 2ab \cos{C}. \end{align} \]
In particular, when an angle is a right angle, the cosine term of one of the equations vanishes, causing it to reduce to the Pythagorean theorem.
Trigonometric Functions in the Complex Plane
Euler's formula, which says that \[ e^{ix} = \cos{x} + i \sin{x} \] for complex \( x \), extends the domain of the trigonometric functions to the complex numbers.
Due to the evenness and oddness of cosine and sine, respectively, \[ e^{-ix} = \cos{x} - i \sin{x}, \] so \[ e^{ix} + e^{-ix} = 2 \cos{x}. \] It follows that \[ \cos{x} = \frac{e^{ix} + e^{-ix}}{2},\] and similarly \[ \sin{x} = \frac{e^{ix} - e^{-ix}}{2i} \] and \[ \tan{x} = \frac{e^{ix} - e^{-ix}}{i(e^{ix} + e^{-ix})}. \]
Solve \( \cos{x} = 2 \) in the complex numbers.
Taking \( \cos{x} = \frac{e^{ix} + e^{-ix}}{2} \) yields
\[ \begin{align*} e^{ix}+e^{-ix} &= 4 \\ \big(e^{ix}\big)^2-4e^{ix}+1 &= 0 \\ e^{ix} &= 2\pm \sqrt{3} \\ x &= -i \ln\big(2\pm \sqrt{3}\big).\ _\square \end{align*} \]
Euler’s formula also allows for the derivation of several trigonometric identities quite easily. Starting with
\[ e^{i(x \pm y)} = \cos(x \pm y) + i \sin(x \pm y), \]
one finds
\[\begin{align*} e^{i(x \pm y)} &= e^{ix} e^{\pm iy} \\ &= (\cos{x} + i\sin{x})(\cos{y} \pm i \sin{y}) \\ &= \cos{x} \cos{y} \mp \sin{x} \sin{y} + i(\sin{x} \cos{y} \pm \cos{x} \sin{y}). \end{align*} \]
Equating the real and imaginary parts, respectively, yields the familiar sum and difference formulas
\[ \cos(x \pm y) = \cos{x} \cos{y} \mp \sin{x} \sin{y} \]
and
\[ \sin(x \pm y) = \sin{x} \cos{y} \pm \cos{x} \sin{y}. \]
Hyperbolic Trigonometric Functions
Besides the standard set of trigonometric identities discussed above, there are also the hyperbolic trigonometric functions. These include
- \(\sinh x = \frac{e^x - e^{-x}}{2}\)
- \(\cosh x = \frac{e^x + e^{-x}}{2}\)
- \(\text{sech } x = \frac{1}{\cosh x}\)
- \(\text{csch } x = \frac{1}{\sinh x}\)
- \(\tanh x = \frac{\sinh x}{\cosh x}\)
- \(\coth x = \frac{1}{\tanh x}\).
They are so called, due to the similar properties they share with the similarities to their trigonometric counterparts.
This can be seen in some of the relations of the hyperbolic trigonometric functions:
- \(\cosh^2 x - \sinh^2 x = 1\)
- \(\tanh^2 x + \text{sech}^2 x = 1\)
- \(\coth^2 x - \text{csch}^2 x = 1\)
- \(\sinh (x + y) = \sinh x \cosh y + \cosh x \sinh y\)
- \(\sinh (x - y) = \sinh x \cosh y - \cosh x \sinh y\)
- \(\cosh (x + y) = \cosh x \cosh y + \sinh x \sinh y\)
- \(\cosh (x - y) = \cosh x \cosh y - \sinh x \sinh y\).
The hyperbolic forces are seen in a variety of areas. For example, if you let a rope hang freely while tied at two ends, it will form a hyperbolic cosine function.
Or, if you add two velocities relativistically, \((\)i.e. \(v_1\) with respect to you, and \(v_2\) with respect to \(v_1),\) you get
\[\tanh^{−1}\left(\frac{v}{c}\right)=\tanh^{−1}\left(\frac{v_1}{c}\right)+\tanh^{−1}\left(\frac{v_2}{c}\right).\]

