Cuckoo Filter
The Cuckoo Filter is a probabilistic data structure that supports fast set membership testing. It is very similar to a bloom filter in that they both are very fast and space efficient. Both the bloom filter and cuckoo filter also report false positives on set membership.
Cuckoo filters are a new data structure, described in a paper in 2014 by Fan, Andersen, Kaminsky, and Mitzenmacher[1]. Cuckoo filters improve upon the design of the bloom filter by offering deletion, limited counting, and a bounded false positive probability, while still maintaining a similar space complexity. They use cuckoo hashing to resolve collisions and are essentially a compact cuckoo hash table.
Cuckoo and bloom filters are both useful for set membership testing when the size of the original data is large. They both only use 7 bits per entry. They are also useful when an expensive operation can be avoided prior to execution by a set membership test. For example, before querying a database, a set membership test can be done to see if the desired object is even in the database.
Contents
Overview
The cuckoo filter is a minimized hash table that uses cuckoo hashing to resolve collisions. It minimizes its space complexity by only keeping a fingerprint of the value to be stored in the set. Much like the bloom filter uses single bits to store data and the counting bloom filter uses a small integer, the cuckoo filter uses a small \(f\)-bit fingerprint to represent the data. The value of \(f\) is decided on the ideal false positive probability the programmer wants.
The false positive probability is very important for bloom filters and cuckoo filters. Here is the analysis for the bloom filter. These filters will always return a false positive with some probability. Cuckoo filters are constructed with some desired false positive probability. This desired probability is used to choose other variables in the filter.
The cuckoo filter has an array of buckets. The number of fingerprints that a bucket can hold is refered to as \(b\). They also have a load which describes the percent of the filter they are currently using. So, a cuckoo filter with a load of 75% has 75% of its buckets filled. This load is important when analyzing the cuckoo filter and deciding if and when it needs to be resized.
The following gif shows how a cuckoo filter might insert some elements. The \(f\) value of the fingerprint is 7, and the \(b\) is 2. This gif shows how inserting an element three times would cause the cuckoo filter to use the secondary bucket. Notice also how the false positive probability (FPP) increases with each insert.
 Cuckoo filter with 7-bit fingerprints and a bucket size of 2
Cuckoo filter with 7-bit fingerprints and a bucket size of 2
One final optimization used by cuckoo filters is that they use semi-sort. Semi-sort is a technique to save space that utilizes the fact that the order of fingerprints in a given bucket do not matter. They can compress the buckets by first sorting the fingerprints in them, then storing another fingerprint of that result. This technique saves 1 bit per fingerprint and is the reason behind the cuckoo filter's bits-per-entry equation below.
Cuckoo Hashing
Cuckoo hashing is type of collision handling in hash based data structures. Collision handling is what happens when a key is hashed to a bucket that already has a value in there. The method by a hash table handles these collisions is a property of the table, and cuckoo hash tables use cuckoo hashing.
 Cukoo hashing: each letter has two possible buckets. Here, B would have to move down.[2]
Cukoo hashing: each letter has two possible buckets. Here, B would have to move down.[2]
Cuckoo hashing got its name from the cuckoo bird. Cuckoos are known for laying their eggs in other birds' nests. When those baby cuckoo hatch, they attempt to push any other eggs or birds out of the nest. This is the basic principle of cuckoo hashing.
In cuckoo hashing, each key is hashed by two different hash functions, so that the value can be assigned to one of two buckets. The first bucket is tried first. If there's nothing there, then the value is placed in bucket 1. If there is something there, bucket 2 is tried. If bucket 2 if empty, then the value is placed there. If bucket 2 is occupied, then the occupant of bucket 2 is evicted and the value is placed there.
Now, there is a lone (key, value) pair that is unassigned. But, there are two hash functions. The same process begins for the new key. If there is an open spot between the two possible buckets, then it is taken. However, if both buckets are taken, one of the values is kicked out and the process repeats again.
It is possible to encounter an infinite loop in the process of removing and moving keys. Because of this, it is important to keep track of every bucket you visit. If the same bucket is visited twice, there is a cycle. The only way to fix it is to rebuild the hash table, making it bigger or changing the hash functions.
The following image shows an empty cuckoo filter. There are 6 buckets and 2 hash functions. The hash functions are shown. The following 5 numbers are inserted into the hash table.
[3, 7, 14, 15, 19]
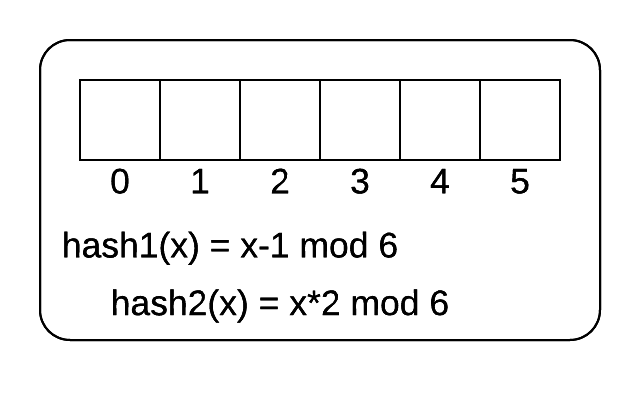 Cukoo filter
Cukoo filter
For reference, here is how the cuckoo filter works:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
Fill your answer in as a list of numbers. Leave a list slot empty if the corresponding bucket in the cuckoo table stays empty.
Partial-Key Cuckoo Hashing
Though cuckoo filters are based on cuckoo hashing, they actually use a derivative of that which the inventors call partial-key cuckoo hashing. In a regular cuckoo hash table, if something is hashed to its first possible bucket and that bucket is empty, it is hashed by another hash function and moved to a second bucket. However, in the cuckoo filter, only \(f\)-bit fingerprints are stored. So, if a fingerprint needs to be kicked out, it's alternate bucket needs to be able to be found. Partial-key cuckoo hashing works like this:
- Insert key \(k\).
- Compute the hash of \(k\), \(h(k) = k_h\) using the first hash function.
- If the first bucket is empty, place \(k_h\) in that bucket.
- If the first bucket is not empty, computer the hash of \(k_h\), \(g(k_h) = k_{h_g}\) using the second hash function.
- XOR \(k_{h_g}\) with \(k_h\) to get the value of the second bucket \(k_g\).
- Look to that second bucket to complete cuckoo hashing.
The upside of this process is given a fingerprint and a bucket, it is easy to compute the location of the other bucket. This allows cuckoo filter to store very small \(f\)-bit fingerprints and save space. However, the downside of this process is that if the fingerprint is \(f\) bits, the second bucket is chosen from \(2^f\) possibilities. It's not random like it should be in hash tables.
This is actually a huge point of contention concerning cuckoo filters. In theory, it has been proven that cuckoo filters won't work due to their unrandomized hash functions. The smaller the fingerprint, \(f\), the fewer choices each key has for their pair of buckets, and the higher a chance of collisions. The lower bound on fingerprint size becomes \(\Omega(n)\). Note that we using \(\Omega\) here to denote the lower bound.
Oddly enough, though cuckoo filters have been shown to be terrible in theory, they tend to work in practice. In fact the lower bound of fingerprint size above excludes some constant factors. In fact, it is \(\Omega(n)/2b\), where \(b\) is the number of keys a bucket can hold in the cuckoo filter. Even when \(b\) equals 4, this covers a wide range of \(n\), and fingerprints can be a reasonable size.
Empirical analysis was performed on the cuckoo filter. Various values of \(n\), \(b\), and \(f\) were tested to see how they would affect the load of the cuckoo filter. When \(b = 4\), cuckoo filters achieved 95% load. \(f = 7\), however, was the optimal property for the cuckoo filter. Once the fingerprint was 7 bits long, the load factor of the cuckoo filter mirrored that of a cuckoo hash table that used two perfectly random hash functions.
Deeper analysis of partial-key cuckoo hashing is an open question. Further evaluation might lend more theoretical credibility to the data structure in the future.
Time Complexity
The time complexity of cuckoo filters follows from the time complexity of cuckoo hashing.
| Operation | Time Complexity |
| lookup | \(O(1)\) |
| deletion | \(O(1)\) |
| insertion | \(O(1)\)** |
**amortized expected, with reasonably high probability if load is well managed.
Lookup and Deletion
Lookup and deletion are \(O(1)\) operations in cuckoo hashing, and the same is true for cuckoo filters. There are a maximum of two locations (or however many hash functions you use) to check. If found, the appropriate operation can be performed in \(O(1)\) time as well, making these both constant time operations.
Insertion
Proving the insertion complexity is tricky and longer, so it's included below.
Cuckoo vs Bloom Filters
Cuckoo filters improved upon the design of the bloom filter by allowing deletion from the set. Counting Bloom Filters had already been proposed as a way of modifying the bloom filter to allow deletions. However, counting bloom filters come with their own set of disadvantages.
There are four ways to compare cuckoo filters, bloom filters, and counting bloom filters: the time complexity of their operations, their false positive probabilities, their space complexity, and their capacity.
Time Complexity
Cuckoo filters are generally slower than bloom filters and counting bloom filters regarding insertion. Though cuckoo filters have an \(O(1)\) amortized insertion time, the bloom filter and counting bloom filter have a truly constant time insertion complxity of \(O(k)\). It is based solely on the number of hash functions, \(k\). Additionally, the insertion time of the cuckoo filter increases as load increases and the probability of a necessary resize of the filter increases.
Lookup is faster in a cuckoo filter than in a bloom filter or a counting bloom filter. There are only two locations to check in a cuckoo filter, so this operation is \(O(1)\). Bloom filters and counting bloom filters require \(O(k)\) to do so. By this same logic, deletion is faster in a cuckoo filter than in a counting bloom filter.
False Positive Probability
The false positive probability of a cuckoo filter will trend towards the desired false positive probability as the load of the filter increases. On the other hand, the false positive probability in a bloom filter or a counting bloom filter will trend towards 100% as their loads increase. It is up to the implementer of those filters to decide when to resize the bloom filter to reduce the false positive probability.
Space Complexity
The space complexity of the counting bloom filter is worse than both the cuckoo filter and the bloom filter because the space per bucket needs to be multiplied by the counter. With regards to the cuckoo and bloom filters, they perform differently at different false positive probabilities. When the false positive probability of the filter is less than or equal to 3%, the cuckoo filter has fewer bits per entry. When it is higher, the bloom filter has fewer bits per entry.
| Filter | Bits Per Entry |
| Cuckoo | \(\frac{\log(\frac{1}{FPP}) + 2}{load}\) |
| Bloom | \(1.44 \log(\frac{1}{FPP})\) |
Capacity
Cuckoo filters and bloom filters are different in how they handle increased load. As the cuckoo filter increases load, insertions are more likely to fail, and so its time complexity increases exponentially. However, the false positive rate remains the same. Bloom filters can keep inserting items into the filter at the cost of an ever rising false positive rate.
The capacity of the bloom filter is theoretically 100%, but it have a terrible false positive probability. Cuckoo filters can maintain a stable false positive rate if the number of bits per entry is around 7 and if the load is around 95.5%.
\[\frac{\log(\frac{1}{FPP}) + 2}{load} = \frac{\log(\frac{1}{.03}) + 2}{.955} \approx 7\]
Proving Insertion Time
In cuckoo hashing, inserting an element seems like much worse than \(O(1)\) in the worst case because there could be many instances of needed to remove a value in order to make room for the current value. Plus, if there is a cycle then the entire table must be rehashed.
Note: this proof will be done assuming two hash functions are used in the cuckoo hash table, though it can be generalized to more. The theoretical analysis of cuckoo filters is still underdeveloped, so parts of this proof may gloss over some areas.
To prove this complexity, it is helpful to think about the cuckoo hash table as a graph. The cuckoo graph is made by copying the structure of the first hash table over to a second hash table. Each bucket in these two tables becomes a node in the cuckoo graph. Then, for each key in the original hash table, an edge is drawn from the bucket in table 1 where the first hash function hashes the key to the bucket in table 2 where the second hash function hashes the key. The process of making the cuckoo graph looks like this.
Making a cuckoo graph from a cuckoo table
Claim 1: The first idea from this new, bipartite graph is that an insert will fail if there are more than two cycles in the graph. If there are \(k\) nodes in the graph (buckets), then there need to be \(k + 1\) edges (keys) in order to make two cycles. \(k + 1 \gt k\), so there are too many elements to fit in the buckets and the insertion will fail.
Claim 2: The second idea to take away from this graph is that an insertion will succeed if there a zero or 1 cycles in the graph. If there are zero cycles, then the chain of displaced elements will eventually come to rest. However, with 1 cycle, the chain can still come to rest. Once the chain of displaced elements has gone through the entire first cycle, what remains of the bipartite graph is a tree (a graph with no cycles). So, the nodes within the first either come to rest, or they kick out a certain element that eventually stabilizes elsewhere in the remaining graph.
Claim 3: The final idea that is important in this graph is that an element is inserted into a connected area of the graph with \(k\) nodes (buckets), then it will displace at most \(2k\) nodes to be inserted. This idea follows from the logic of the bipartite graph, where there are twice as many nodes \(2k\) as buckets that created them \(k\).
Now that it is proven that an insertion fails if and only if there are two or more cycles in the cuckoo graph, the probability that there are two or more cycles is needed. When the number of edges \(m\) is much less than the number of nodes \(n\) in a bipartite graph, then the probability, given a path of length \(k\), that it is a cycle is
\[P(k) \leq (\frac{2m}{n^2})^k .\]
This is because, for the cycle, the probability that some edge takes the first spot is \(2m/n^2\). The probability that a second edge takes the second spot is \(2(m-1)/n^2\), and so on. The number of \(k\) length cycles is also at most \(n^k\). So, overall, there are at most \((2m/n^2)^k \cdot n^k\) cycles of length \(k\).
If an insertion is successful, it is because it found path of length \(k\) that was not a cycle. This is found with probability less than or equal to \((2m/n^2)^k \cdot n^k = (2m/n)^k\). This is expected constant time when \(m \ll n\) and logarithmic time with high probability.
The probability that an insertion is unsuccessful is the probability that the connected component of size \(k\) has two or more cycles. This is, given the ends of the edge on which we are inserting,
\[(2m/n^2)^{k-1} \cdot n^{k-2} = O(1) ,\]
when \(m \ll n\).
This can be proven with much stronger proofs, but they are complicated and unwieldy. Now, everything besides the resizing of the hash table has been proven to be \(O(1)\). When the table is resized \(O(n)\) work must be done. However, there have already been \(n\) \(O(1)\) inserts. This makes the amortized cost to resize the table \(O(1)\).
The relationship between \(m\) and \(n\) is optimized when \(m = (1 + \epsilon)n\) for some small \(\epsilon\). When this relationship holds, the probability that there is a connected component of the graph with two or more cycles is \(O(1)\). When this happens, the load factor of the cuckoo table is \(\frac{n}{2m} = \frac{1}{2+2\epsilon} = 1/2\). This means that rougly half of the table is full. When this capacity is exceeded, the need to resize occurs more frequently. A similar proof can be used to show than when 3 hash functions are used, 91% of the table is usable.
References
- Fan, . Cuckoo Filter: Practically Better Than Bloom. Retrieved August 22, 2016, from https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf
- Pagh, R. Wikipedia Cuckoo Hashing. Retrieved August 1, 2016, from https://en.wikipedia.org/wiki/Cuckoo_hashing