Electron Configurations

Electron configuration of an atom tells us how the electrons are arranged in various shells of the atom. It gives an idea of its valency, which will decide how an atom will react with other atoms. The most simple system to determine the electron configuration is the $\text K,\text L,\text M,\text N$ system, devised by Bohr.

According to this, the shells of an atom are named as $\text K,\text L,\text M,\text N, . . . ,$ etc., or $1, 2, 3, 4, . . . ,$ etc., and the maximum number of electrons that can be accommodated is given by the formula $2n^2,$ where $n=(\text{number of the shell})$. For example, the $3^\text{rd}$ shell can accommodate $2\times 3^2=18$ electrons. To be familiar with the valency, you are requested to read Octet Rule.

We have to construct the wave function for a system of identical particles so that it reflects the requirement that the particles are indistinguishable from each other. Mathematically, this means interchanging the particles occupying any pair of states should not change the probability density of the system. This simple statement has the enormous consequence of dividing all particles in nature into one of two classes.

An example for two non-interacting identical particles will illustrate the point. The probability density of the the two particle wave function must be identical to that of the the wave functions that have been interchanged.

In fact, all particles with half integer spins, such as electrons, protons, neutrons, etc., are described by anti-symmetric wave functions and obey the exclusion principle. These particles are called fermions because they obey a statistical distribution law discovered by Fermi and Dirac. Particles with integer spins, such as photons, alpha particles, etc., are described by symmetric wave functions and do not obey the exclusion principle. These particles are called bosons because they follow Bose-Einstein statistics.

This rule states that two particles with half integer spins cannot occupy the same quantum state at the same time. In other words, two electrons moving in an orbital cannot have the same spin quantum number or simply spin.

Half integer spin: A spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin.

For example, in a helium atom, we have two electrons, and they are not present in the same spin, i.e. a helium atom:

$$\begin{aligned} \text{would be like this: }\ce{_2He}:& \ \ \boxed{\uparrow\downarrow}\\ \text{and not like this: } \ce{_2He}:& \ \ \boxed{\uparrow\uparrow} \end{aligned}$$

Note: The spin quantum number has two values $\frac{1}{2}$ and $-\frac{1}{2},$ which means that the spin of an electron can be clockwise represented as $\uparrow$, or anti-clockwise represented as $\downarrow$.

Main Article: orbitals and quantum numbers.

The quantum numbers govern how the particles behave under certain environmental conditions, and they also describe how an electron behaves in a certain orbital. From the Pauli's exclusion principle, we know that two particles cannot be present in the same quantum state, and thus there are a set of $4$ quantum numbers which distinguish the quantum behavior of an electron. They are listed as follows:

1. principal quantum number:
The principal quantum number points the energy level at which the electron is present. It is denoted by the letter $n$, where the value of $n\in \mathbb N,$ the natural numbers. So, as the value of the principle quantum number increases, the energy level also increases, and thus the values $n$ indicate the shell (will be discussed soon) in which the electron is present. For instance,

$$\begin{array}{|c|c|c|c|c|} \hline \text{Value of }n&1 &2& 3 & \cdots\\ \hline \text{Designation of the Shell}& \text K &\text L & \text M & \cdots\\ \hline \end{array}$$

2. angular quantum number:
The angular momentum quantum number is a quantum number that describes the shape of an orbital and tells us which subshells are present in the principal shell. It is denoted by the letter $l$, where the value it takes is from $0$ to $(n-1)$; that is, if the principle quantum number of an electron is $n,$ then the possible values would be $$l=0,1,2,3,\cdots,(n-1).$$

Find the possible values of the angular quantum number if the electron is present in the $\text M$ energy level.

---

As the electron is in the $\text M$ shell, it means that the value of its principle quantum number is $3$. Thus the possible angular quantum number values of the electron would be from $0$ to $(3-1)=2$:

$$l=0,1,2.\ _\square$$

But what do these values represent? As said earlier, it represents the subshell (will be discussed soon) in which the electron is present.

$$\begin{array}{|c|c|c|c|c|} \hline \text{Value of }l&0 &1 & 2 & 3 & \cdots\\ \hline \text{Designation of the Subshell}& \text s &\text p & \text d & \text f & \cdots\\ \hline \end{array}$$

3. magnetic quantum number:
The magnetic quantum number tells us about the orbital that an electron occupies--it determines how many orbitals there are as well as their orientation within a subshell. It is denoted by $m_l,$ which visualizes the behavior of an electron under the influence of a magnetic field (like earth).

We know that the movement of electric charge can generate a magnetic field, and under the influence of an external magnetic field the electrons tend to orient themselves in certain regions around the nucleus (called orbitals), which is why this quantum number gives the number of orbitals in a particular subshell. The values of the magnetic quantum number depends upon the angular quantum number $(l)$. For example, if the angular quantum number of an atom is $l$, then the magnetic quantum numbers range as follows:

$$m_l= -l,( -l+1), . . . , 0 , . . . (l-1), l.$$

So, there are $2l+1$ values of $m_l$ for a given value of $l$, i.e. there will be $2l+1$ orbitals.

Find all possible values of the magnetic quantum number for an electron present in the $\text M$ shell.

---

As seen earlier, the principle quantum number of an electron present in the $\text M$ shell is $3$. The values of $l$ when $n=3$ were $l=0,1,2$. So, the values of $m_l$ when $n=3$ will be as follows:

$$\begin{array}{|c|c|} \hline \text{Values of }l & \text{Values of }m_l\\ \hline l=0 & m_l = 0\\ \hline l=1 & m_l = -1, 0, 1\\ \hline l=2 & m_l = -2, -1, 0, 1, 2\\ \hline \end{array}$$

4. spin quantum number:
In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum (or spin angular momentum, or simply spin) of a given particle. It is denoted by $m_s$ or rarely as $m_{m_l}$. It was found that the electrons not only revolve around the nucleus but also spin around their own axes, and thus the spin quantum number got its own significance.

The spin of an electron can only be, obviously, two types, clockwise or counter clockwise, and the values of the spins are denoted by $\frac 12$ when it is clockwise, and $-\frac 12$ when counter clockwise. Sometimes it is also denoted by the arrows:

$$\begin{array}{|c|c|} \hline \text{clockwise} & \uparrow\\ \hline \text{counter-clockwise} & \downarrow\\ \hline \end{array}$$

According to quantum mechanics, each shell of an atom is defined as an energy level. The shells are as follows:

$$1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, \ldots.$$

The electronic configuration of an electron in a particular shell is denoted by

$$pA^x,$$

where $p$ is the principle quantum number, $A$ is the angular quantum number, and $x$ is the number of electrons in the shell.

Image to help us remember the order in which the electron's are filled up

It also helps in writing the electronic configuration of any specific element. For example, $\ce{_10Ne}$ - $1s^{2}2s^{2}2p^{6}$.

This rule says that the electrons occupy the lowest possible energy level before proceeding to the higher level. The order of increasing energy level is given by the $n+l$, where

$$(n+l)=(\text{principal quantum number}) + (\text{azimuthal quantum number}).$$

The rule is based on the total number of nodes in the atomic orbital, $n + ℓ$, which is related to the energy. In the case of equal $n + ℓ$ values, the orbital with a lower $n$ value is filled first. The fact that most of the ground state configurations of neutral atoms fill orbitals following this $n + ℓ$, $n$ pattern was obtained experimentally, by reference to the spectroscopic characteristics of the elements.

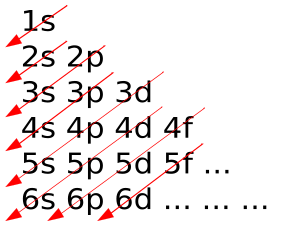Pictorial representation of the Aufbau Principle

This lays the corner stone for the internal arrangement of electrons in an atom, it deals with the order of filling the electrons into the orbitals of the same subshell. When more than one orbital of equal energy are available (e.g. $p_x, p_y, p_z$), the electrons first occupy the orbitals with parallel spins or same spin. Only then the pairing of electrons will take place.

This happens because if we place two electrons in the same orbital with opposite spins, the repulsive nature increases; however, if the electrons are placed in separate orbitals with parallel spins, the repulsion is greatly minimized. Also, the electrons occupy the orbitals with same spin, thus reducing the repulsion.

Let's have a look at the examples of nitrogen and oxygen:

If we follow the Hund's rule for the nitrogen atom, its electronic configuration would be like this: $$\ce{_7N}:\underbrace{\boxed{\uparrow\downarrow}}_{\text{1s}}\quad\underbrace{\boxed{\uparrow\downarrow}}_{\text{2s}}\quad\underbrace{\boxed{\uparrow\color{#FFFFFF}{\downarrow}}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}}_{\text{2p}} \ \ \ (\text{total spin of unpaired electrons}) = \dfrac 12+\dfrac 12+\dfrac12=1\dfrac12.$$

Note that the electrons are placed in orbitals with parallel spins and are not paired up before at least one electron occupies each orbital.

But we can't place the electrons with opposite spin (as in the case below) or start pairing up electrons before filling up each orbital with at least one electron (as in the next case):

$$\begin{aligned} \ce{_7N}:\underbrace{\boxed{\uparrow\downarrow}}_{\text{1s}}\quad\underbrace{\boxed{\uparrow\downarrow}}_{\text{2s}}\quad\underbrace{\boxed{\uparrow\color{#FFFFFF}{\downarrow}}\boxed{\color{#FFFFFF}{\uparrow}\downarrow}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}}_{\text{2p}}& \ \ \ (\text{total spin of unpaired electrons}) = \dfrac 12-\dfrac 12+\dfrac12=\dfrac12.\\ &\text{or}\\ \ce{_7N}:\underbrace{\boxed{\uparrow\downarrow}}_{\text{1s}}\quad\underbrace{\boxed{\uparrow\downarrow}}_{\text{2s}}\quad\underbrace{\boxed{\uparrow\downarrow}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}\boxed{\color{#FFFFFF}{\uparrow}\color{#FFFFFF}{\downarrow}}}_{\text{2p}}& \ \ \ (\text{total spin of unpaired electrons}) = \dfrac12. \end{aligned}$$

Observe that the total spin of the unpaired electrons is maximum in the correct configuration, which is why this rule is also called Hund's rule of maximum multiplicity, the multiple being the spin of the electron i.e. $\frac12$.

The electrons in the oxygen atom are arranged in the following way which obeys the Hund's rule. The electrons in the $p$ orbital are first filled up with at least one electron (in parallel spin) and only then the last electron is paired up:

$$\ce{_8O}:\underbrace{\boxed{\uparrow\downarrow}}_{\text{1s}}\quad\underbrace{\boxed{\uparrow\downarrow}}_{\text{2s}}\quad\underbrace{\boxed{\uparrow\downarrow}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}\boxed{\uparrow\color{#FFFFFF}{\downarrow}}}_{\text{2p}}\ \ \ (\text{total spin of unpaired electrons}) =\dfrac12+\dfrac 12 = 1,$$

as opposed to this one where the pairing up has taken place in the wrong order, disobeying Hund's rule:

$$\ce{_8O}:\underbrace{\boxed{\uparrow\downarrow}}_{\text{1s}}\quad\underbrace{\boxed{\uparrow\downarrow}}_{\text{2s}}\quad\underbrace{\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\color{#FFFFFF}{\downarrow}\color{#FFFFFF}{\downarrow}}}_{\text{2p}}\ \ \ (\text{total spin of unpaired electrons}) =0.$$

Again observe that the total spin of the unpaired electrons is maximum in the correct configuration.