Four Color Theorem

The four color theorem states that any map--a division of the plane into any number of regions--can be colored using no more than four colors in such a way that no two adjacent regions share the same color. 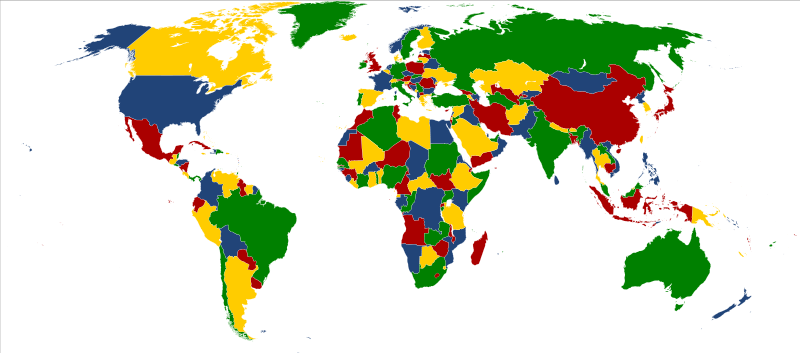A map of the world, colored using four colors The four color theorem is particularly notable for being the first major theorem proved by a computer.

Interestingly, despite the problem being motivated by mapmaking, the theorem is not especially important to the field as most maps were historically drawn with more than four colors (despite only four being necessary). In addition, most maps occurring in practice only require three colors.

While maps can informally be understood as a collection of possibly adjacent countries, it is necessary that every country be contiguous/connected, roughly meaning that it is possible to walk from any point in a country to any other point in a country without ever leaving the country. In practice, this is not necessarily the case: for example, the state of Michigan consists of two disconnected regions.

There are also counterexamples involving maps of finite area and infinite perimeter, such as the Koch snowflake. They are generally ignored when detailing the theorem, as they are not very interesting examples.

A more formal statement results from graph theory. If each country is represented by a vertex, and two vertices are connected by an edge if and only if they are adjacent, the result is a planar graph. Furthermore, it can be shown that there exists a map corresponding to any planar graph, so the theorem can be understood as a result on planar graphs. More specifically, the four color theorem states that

The chromatic number of a planar graph is at most 4.

The five color theorem is obviously weaker than the four color theorem, but it is much easier to prove. In fact, its earliest proof occurred "by accident," as the result of a flawed attempt to prove the four color theorem. It proceeds as follows:

Consider a planar graph \(G\). It can be shown that \(G\) must have a vertex \(v\) shared by at most 5 edges (*). Consider the graph \(G'\) formed by removing \(v\) and all edges from \(v\) from \(G\). \(G'\) is still planar, so it can be assumed by induction that \(G'\) can be colored with five colors.

If \(v\) was connected to at most four vertices, the result is immediately true since \(v\) is simply assigned any color different from its neighbors, resulting in a 5-coloring of \(G\) as desired. Thus, the only important case is where \(v\) is connected to five vertices \(v_1, v_2, v_3, v_4, v_5\) (in, say, clockwise order), and those five vertices are colored with five different colors \(c_1, c_2, c_3, c_4, c_5\).

Now consider all the vertices colored with \(c_1\), all the vertices colored with \(c_3\), and all the edges between them. If \(v_1\) and \(v_3\) are disconnected in this subgraph, the component containing \(v_1\) can be colored in the reverse way (all vertices colored \(c_1\) in this component are recolored with \(c_3\), and vice versa), at which point \(v\) can be colored with \(c_1\) to end the proof. Thus the only important case occurs when \(v_1\) and \(v_3\) are connected in this subgraph.

Now consider all the vertices colored with \(c_2\), all the vertices colored with \(c_4\), and all the edges between them. By the same logic, the only important case occurs when \(v_2\) and \(v_4\) are connected in this subgraph. But since \(v_1\) is connected to \(v_3\), \(v_2\) cannot be connected to \(v_4\) without breaking the planarity of the graph (recall that \(v_1, v_2, v_3, v_4, v_5\) are listed in clockwise order for a given orientation of \(G\)). Therefore, all cases have been covered, and the result follows from induction. \(_\square\)

The icosahedral graph has each vertex connected to five others

It's natural to ask why this proof doesn't hold for the four color theorem as well, as it seems the fifth color played very little role here. In fact, the logic would be completely valid, except for the statement of (*). In particular, it is not necessarily true that \(G\) has a vertex connected to at most four edges; for example, the graph corresponding to an icosahedron is planar and has every vertex connected to five others.

Unlike the five color theorem, the four color theorem is extremely difficult to prove. In fact, though the problem was first rigorously formulated in 1852, it was not until 1976 that a correct proof was first published. Due to the nature of the problem, there were an unusually large number of failed approaches: for example, Kempe gave a proof in 1879 that stood for 11 years before being refuted; still, it led to the proof of the five color theorem above.

The eventual proof utilized minimality: it was shown that any counterexample must contain one of a set of graphs as a subgraph, but that if any of those subgraphs were part of a counterexample, a smaller counterexample existed. This demonstrated the result by showing that there cannot be any smallest counterexample, so there cannot be any counterexample at all.

More formally,

• An unavoidable set is a set of graphs such that any smallest counterexample to the four color theorem must contain at least one of the graphs as a subgraph.
• A reducible configuration is a graph with the following property: any map containing a reducible configuration can be reduced to a smaller map, satisfying the condition that if the smaller map can be colored with 4 colors, the original map can also be colored with 4 colors.

If an unavoidable set of reducible configurations could be found, then it would suffice to show that every graph in that set could be four-colored. This is precisely what the 1976 proof achieved, showing that there existed an unavoidable set of reducible configurations with size 1936. Checking these configurations took over 1000 hours on a supercomputer.

The four color theorem can be extended to infinite graphs for which every finite subgraph is planar, which is a consequence of the De Bruijn-Erdos theorem:

An infinite graph \(G\) can be colored with \(k\) colors if and only if every finite subgraph of \(G\) can be colored with \(k\) colors. \(_\square\)

This result has key application to the chromatic number of the plane problem, which asks how many colors are needed to ensure every point in the plane does not share a color with any point a unit distance away from it. In particular, this result shows that the chromatic number of the plane is between 4 and 7 inclusive.

It is also worth considering coloring divisions of surfaces other than the plane. Since the plane can be mapped to a sphere, the four color theorem applies to a sphere as well, essentially saying that any map on a globe can be colored with at most four colors. However, stranger surfaces require more colors: for example, divisions of the Klein bottle and Möbius strip both require 6 colors.

Finally, none of these results extend to three dimensions: it is relatively easy to contrive an example in which every pair of \(n\) flexible rods are adjacent, and so they require \(n\) colors for any arbitrary integer \(n\). Thus, there is no analogue to the four color theorem in higher dimensions.

• Graph theory