Game Theory
Game theory is the mathematical analysis of decision making. In game theory, the interaction between two or more players is often framed in terms of a game with a particular set of rules. Of interest may be the strategies that give optimal outcomes for each of the players or, conversely, the resulting outcomes when certain strategies are played. Many phenomena in business, politics, and evolutionary biology, for instance, can be modeled as games.
After coming to prominence in the latter half of the twentieth century, game theory has led to several Nobel Prizes in economics, as well as significant advances in biology, computer science, and political science.
Basic concepts: the prisoner's dilemma
Interactions in game theory are generally modeled in terms of well defined games between two or more players. To illustrate, consider the following simple game, commonly known as the prisoner's dilemma, played between Alice and Bob.
Prisoner's dilemma. The police have captured two criminals and are interrogating them in separate rooms, so they can't communicate with each other. They offer each the following deal:
- If Alice snitches on Bob, Alice goes free and Bob spends three years in jail. (Alice defects, Bob cooperates)
- Similarly, if Bob snitches on Alice, Bob goes free and Alice spends three years in jail. (Alice cooperates, Bob defects)
- If neither of them snitch on each other, then they both spend one year in jail. (Mutual cooperation)
- If they both snitch on each other, then they both spend two years in jail. (Mutual defection)
In the prisoner's dilemma, Alice and Bob each choose a strategy, defect or cooperate, for a total of four possible combinations, each of which corresponds to an outcome, or payoff. One can thus draw the following payoff matrix, which illustrates the payoff for each combination of strategies. (In the figure below, the ordered pair \( (-B, -A) \) indicates that Alice and Bob spend \( A \) and \( B \) years in jail, respectively.)
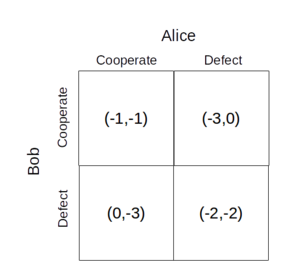
To see why the game is called the prisoner's dilemma, think about what strategy each of the players might elect. Suppose that the goal of each prisoner is solely to minimize his or her time spent in jail and that he or she has no information on what strategy the other player might choose.
Consider the game from Bob's perspective. From the payoff matrix, it is clear that no matter what strategy Alice chooses, Bob minimizes his time spent in jail by defecting. If Alice cooperates, Bob should defect (since he would spend no time in jail instead of one year); and if Alice defects, Bob should also defect (since he would spend two years in jail instead of three). The game, which is symmetric with respect to both players, is the same from the perspective of Alice, who should also defect.
Thus, if both players are rational—that is, if they wish to maximize their payoffs—the game will result in mutual defection. It is said that mutual defection is the game's Nash equilibrium, a set of strategies for which no players can improve their payoffs by changing their strategies. (In general, a game may have multiple Nash equilibria, but the prisoner's dilemma has only one.)
In the sense that mutual defection does not maximize the sum of the players' payoffs, it might be said that the Nash equilibrium in this case is not efficient (specifically, Pareto efficient). The fact that the Nash equilibrium is not also the efficient solution lies at the heart of the prisoner's dilemma.
An example of a game with two Nash equilibria is the stag hunt.
Stag hunt. Two hunters, Alice and Bob, sit awaiting for a stag, which will provide significant sustenance for both hunters when felled. Hares also appear, which will feed one of the hunters if killed. The stag is close by and will eventually come within range of the hunters' bows; however, if the hare is hunted, the hunters will disturb the forest and scare away the stag. Both hunters may hunt hares.
- If only Alice hunts the hare, Alice gains food for a day, and Bob goes hungry. (Alice defects, Bob cooperates)
- Similarly, if only Bob hunts the hare, Bob gains food for a day, and Alice goes hungry. (Alice cooperates, Bob defects)
- If both hunters hunt the stag, which provides one individual with four days' worth of food, then each hunter gains enough food for two days after splitting the spoils. (Mutual cooperation)
- If they both hunt hares, then both gain food for a day. (Mutual defection)
The stag hunt differs from the prisoner's dilemma in that there are two Nash equilibria: both hunters may defect (hunt hares) or cooperate (hunt the stag). Furthermore, both players obtain their optimal outcome by cooperating. It is clear that perfectly rational players will each reason that the other will hunt the stag and that the players will default to mutual cooperation.
However, in real-world situations, a player may be risk averse: he or she may anticipate the other player failing to play the optimal move and thus defect in turn. Imagine, for instance, that the consequence of cooperation when the other player defects was going hungry and dying (i.e., a highly negative payoff). The stag might provide a marginally better payoff than a hare, but each player not be able to tolerate the risk of the other choosing to defect.
Iterated games
In reality, however, when human test subjects are asked to play the prisoner's dilemma, mutual cooperation often results. Does this show that humans are irrational? Perhaps, but it is not hard simply to argue that the simple model presented above fails to capture all the dimensions of the real-world problem. For one, human players may not see the prisoner's dilemma in terms of a simple payoff matrix. Bob, for instance, may decide not to snitch on a fellow prisoner out of a sense of honor.
Even so, simple elaborations on the basic scenario outlined in the prisoner's dilemma can help explain a wide range of behaviors. Consider what happens when individuals play the iterated prisoner's dilemma: suppose Alice and Bob play the prisoner's dilemma \( n \) times in a row. In the case of the iterated game, a strategy is no longer a single move chosen independently of the other player's strategy but, rather, a sequence of moves. Each additional move may be chosen with the previous in mind: for instance, Bob may choose to cooperate if and only if Alice cooperated on the previous move.
For instance, sample strategies might include the following:
- Always cooperate: cooperate on every move.
- Always defect: defect on every move.
- Random: with probability \( 0.5 \), defect; otherwise, cooperate.
- Tit-for-tat: cooperate if the opponent cooperated on the previous move; otherwise, defect. Cooperate on the first move.
With \( n \) fixed, a simple backwards induction argument suffices to show that the Nash equilibrium is to always defect. The last move is the same as the non-iterated prisoner's dilemma: clearly, one should defect on the \( n \)th move because no further moves will be played. Given that mutual defection will be played for the \( n \)th move, then it is also rational to play for the \( (n - 1) \)th move. It follows that both players should defect for every move.
However, if \( n \) is determined probabilistically (perhaps the game has some probability of ending on each move) or infinite, then the "optimal" strategy is not so clear: the set of all possible strategies, the strategy space, is extremely large.
Still, one can make progress by analyzing the iterated prisoner's dilemma through simulation. In 1980, Robert Axelrod solicited entries for an iterated prisoner's dilemma tournament (with the end determined probabilistically). The submissions, which came from both hobbyists and academics alike, specified strategies in the form of computer programs. The clear victor among the fourteen contestants was Anatol Rapoport, who submitted the simplest strategy by far: tit-for-tat. Following on the attention his tournament had garnered, soon after Axelrod ran a second round of his tournament, which attracted over sixty submissions, some rather sophisticated. The victor was once again Rapoport, who had once again submitted tit-for-tat. [1]
More sophisticated means of analyzing the iterated prisoner's dilemma and other iterated games have since been used, but Axelrod's tournament nonetheless provides some heuristic insight into what strategies might prove to be more successful. It turns out to be rather difficult to try to exploit "nice," cooperative strategies because doing so imposes a significant penalty when matched against strategies that reciprocate in kind, such as tit-for-tat. Tit-for-tat fares reasonably well against both highly cooperative and highly defective strategies because it will reciprocate in kind. Although it doesn't do quite as well as highly defective strategies against highly cooperative strategies, tit-for-tat does well against other "tit-for-tat-like" strategies.
The robust nature of tit-for-tat suggests a plausible mechanism for the evolution of cooperation. Many situations in evolutionary biology or the social sciences involve not single-shot prisoner's dilemma games, which would tend to result in non-cooperation, but repeated interactions. Such interactions may be the basis of cooperation engendered by reciprocal strategies similar to tit-for-tat.
Some more types of games
The prisoner's dilemma is only one of many games that are frequently studied. Games need not be played only between two players, and moves need not be simultaneous or even deterministic.
Since what formally constitutes a "game" can be quite broad, it helps to classify games by their various properties.
Players of a game are said to have perfect information if the sequence of moves played by each player is known to all players. A combinatorial game is a deterministic game in which all players have perfect information. Examples include chess, tic-tac-toe, and nim. A combinatorial game is said to be solved when the optimal strategy (if one exists) is known.
A game is said to be a zero-sum game if the sum of the payoffs for all players is constant (including zero). In essence, no player can achieve a higher payoff without decreasing the payoffs of the other players.
A simultaneous game is one in which all players move effectively simultaneously, whereas the moves are non-simultaneous in a sequential game. Chess and tic-tac-toe are sequential. The basic form of the prisoner's dilemma is simultaneous, although one could certainly formulate a form of the iterated prisoner's dilemma in which the moves are staggered (which would be sequential). For the latter case, it would make sense to use a decision tree in which the strategy space and payoffs are drawn on a branched tree enumerating all possible sequences of moves.
 Representation
Representation
Games may also be asymmetric. While both players have an identical choice of moves to be make simultaneously in the prisoner's dilemma, which is symmetric, there are also many examples in which this is not the case. In the ultimatum game, one individual is asked to portion a large sum of money for himself and another player. The second player can then choose to accept or reject the portion that he or she is given.
References
[1] Axelrod, R. "More effective choice in the prisoner's dilemma." The Journal of Conflict Resolution 24: 379-403 (1980).
