Lenz's Law
Lenz's law states that whenever there is a change in the magnetic flux through a conducting loop, a current arises to produce a magnetic field that balances the change, i.e. to keep \(\int_A \vec{B}\cdot \vec{n}\) constant. This is a result of Faraday's law of induction.
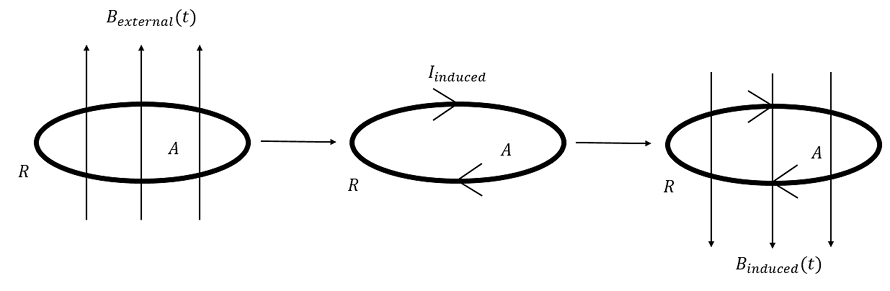 An externally applied magnetic field through an area induces a current. The induced magnetic field due to the induced current opposes the external field by Lenz's law.
An externally applied magnetic field through an area induces a current. The induced magnetic field due to the induced current opposes the external field by Lenz's law.
Lenz's Law and Faraday's Law of Induction
When a magnetic field \(\vec{B}\) goes through a closed conducting loop of area \(A\), it causes a magnetic flux: \[\Phi_B = \vec{B} \cdot \vec{A}\] Here \(\vec{A}\) is the unit vector that points orthogonal to the surface enclosed by the loop everywhere. The dot product above means that a magnetic field at an angle to the loop has less magnetic flux through that loop than if it were orthogonal to the plane of the loop. Formally, if the loop does not lie in a plane, the flux is written as an integral over the surface enclosed by the loop: \[\Phi_B = \int \vec{B} \cdot d\vec{A}\]
If the loop is instead a solenoid or other coil with many turns, each turn of the coil is usually approximated by its circular cross-section and the flux is summed over every turn.
Faraday's law of induction states that when the magnetic flux through a closed conducting loop changes in time, an emf is induced in that loop: \[\varepsilon_{\text{induced}} = -\frac{d\Phi_B}{dt}.\]
Since the loop is conducting, it has some resistance \(R\), and the emf induces a current according to Ohm's law: \[I_{\text{induced}} = \frac{\varepsilon_{\text{induced}}}{R} = -\frac{1}{R} \frac{d\Phi_B}{dt}.\]
In turn, the induced current causes a magnetic field according to Ampere's Law, which itself has a flux through the closed loop. According to Lenz's law, the direction of the induced current and resultantly the induced magnetic flux opposes the original magnetic flux. It is important to note that the direction of the change in flux may be opposite to the direction of the field, for instance, if the strength of the field is decreasing or the field is tilting.
Since the sign of the induced current determines the direction of the induced magnetic flux, the negative sign in Faraday's law is also often referred to as Lenz's law rather than the conceptual statement.
Lenz's law is what allows inductors in circuits to function. Inductors have a large voltage across them when the current is changing rapidly in the circuit. This is because inductors are often solenoids or toroids in which current causes a magnetic flux. When the current changes rapidly, the magnetic flux changes rapidly, and a large emf is induced that opposes the original change in current.
Explain how a simple electric motor works using Lenz's law.
Solution:
As a simple motor, consider a coil of wire that is stationary in a vertical magnetic field such that there is no magnetic flux through the coil:
A coil of wire in a vertical magnetic field. The area vector \(\vec{A}\) for the plane of the wire is perpendicular to the field, so there is no magnetic flux.
If the coil is rotated slightly, the angle between the area vector and the magnetic field is no longer zero. Therefore, the magnetic flux increases in time. By Faraday's law of induction, this induces an emf that causes a current in the coil. This induced current produces a magnetic field that opposes the applied field, since the flux of the applied field is increasing:
As the coil tilts, the area vector \(\vec{A}\) is no longer perpendicular to the applied magnetic field \(\vec{B}\), so the magnetic flux of the applied field increases. This induces an emf and thus a current in the coil which results in an induced magnetic field opposing the applied field.
Recall now that like poles of permanent magnets repel and opposite poles of permanent magnets attract. The reason is derived from the fact that opposite poles have parallel field lines, while like poles have antiparallel field lines. Here, the vertical component of the induced magnetic field from the coil points antiparallel to the applied field, acting as a "like pole." This causes the applied field to push down on the coil, repelling the induced field and causing the coil to spin (provided that the field is weaker on one side of the coil than the other).
Once the coil flips halfway over, the magnetic flux will begin to decrease and the force on the coil will act in the opposite direction To counteract this, one side of the coil is typically covered with insulating material that reduces the amount of current flowing through the coil. As a result, by initially changing the angle of the coil quickly, a very large emf and a large induced magnetic field can be created from the coil that causes the coil to rotate quickly enough to complete a full revolution. The cycle then begins again, driving the coil through another full revolution and so on.
A wire loop in the \(x\)-\(y\) plane sits in an external uniform magnetic field oriented at 30 degrees from the positive \(z\) direction in the \(x\)-\(z\) plane, which increases in strength over time. In which direction does the induced magnetic field at the center of the wire loop point in the \(x\)-\(z\) plane?
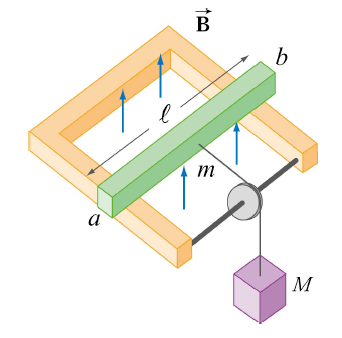 A mass \(M\) pulls the conducting bar through a vertically oriented magnetic field.
A mass \(M\) pulls the conducting bar through a vertically oriented magnetic field.
In the above picture, a mass \(M\) falls under the influence of gravity, pulling with it a conducting bar of mass \(m\), resistance \(R\), and length \(\ell\) that sits on a U-shaped piece of metal in a vertically oriented magnetic field perpendicular to the plane of the U, pointing in the positive-z direction. In which direction does the induced current flow?
Experiment Demonstrating Lenz's Law
A common experiment demonstrating Lenz's law is the "magnet drop" experiment. In this experiment, a(n often powerful, neodymium) magnet is dropped through a conducting tube, often made of copper. The changing magnetic flux as the magnet falls induces a current in the tube which creates a magnetic field opposing the magnetic field of the permanent magnet. Because like poles of a magnet repel and the induced magnetic field appears to be a like pole at either end of the magnet, a magnetic force is exerted on the permanent magnet that slows its fall due to gravity.
![A powerful magnet dropped in a copper tube made to levitate in the tube via Lenz's law; here the short copper tube is rotated repeatedly to keep the magnet suspended [2].](https://d18l82el6cdm1i.cloudfront.net/uploads/h4MOTJI2yo-lenzcopper.gif) A powerful magnet dropped in a copper tube made to levitate in the tube via Lenz's law; here the short copper tube is rotated repeatedly to keep the magnet suspended [2].
A powerful magnet dropped in a copper tube made to levitate in the tube via Lenz's law; here the short copper tube is rotated repeatedly to keep the magnet suspended [2].
A permanent magnet of mass \(M\) is released from rest at the middle of a long copper tube of resistance \(R\) and cross-sectional area \(A\) as above. Make the approximation that the strength of the magnetic field of the permanent magnet falls as in hint 1 below with \(I\) replaced by some constant \(I_0\). Find the velocity of the magnet as a function of time, if the magnet is released at \(t=0\).
Hint 1: The magnitude of a magnetic field caused by a current loop of radius \(\rho\) along the axis of the loop is:
\[B = \frac{\mu_0 I \rho}{2(\rho^2+z^2)^{3/2}}.\]
where \(z\) is the distance along the axis of the loop and \(I\) is the current in the loop.
Hint 2: The force between two magnetic dipole moments is
\[F = |\nabla (\vec{m} \cdot \vec{B})| \]
where the \(B\) field is due to one dipole moment and \(m = IA\) is the the other dipole moment, with \(I\) the effective current and \(A\) the cross-sectional area treating the second dipole as a current loop.
Solution:
At a distance \(r\) down the tube, the magnitude of the rate of change of magnetic flux through a circular cross-section of the tube is:
\[\frac{d\Phi_B}{dt} = A\frac{dB}{dt} = \frac{d}{dt} \left(\frac{\mu_0 I_0 \sqrt{A/\pi}}{2((A/\pi)+r^2(t))^{3/2}}\right) =-\frac{3\mu_0 I_0 r(t) v(t)\sqrt{A} \pi^2}{2(A+\pi r(t)^2)^{5/2}}.\]
where \(I_0\) is a constant that describes the effective strength of the permanent magnet as a magnetic dipole.
The magnitude of the current induced in the copper ring bounding this cross-section is therefore:
\[I(t) = \frac{3\mu_0 I_0 r(t) v(t)\sqrt{A} \pi^2}{2R(A+\pi r(t)^2)^{5/2}}.\]
Below the falling magnet, the magnetic flux is increasing over time. The direction of the current thus creates a magnetic field opposing the field of the permanent magnet, which will manifest itself as a repulsive force. Above the falling magnet, the magnetic flux is decreasing over time. The direction of the current thus creates a magnetic field in the same direction as the permanent magnet, which will manifest itself as an attractive force. These two effects slow the rate of fall of the permanent magnet.
Using hint 2, the force between the dipole moment of a copper ring and the magnetic field of the permanent magnet is:
\[F = AI(t) |\nabla (B(t)| = \frac{3\mu_0 I_0 r(t) v(t)A^{3/2} \pi^2}{2R(A+\pi r(t)^2)^{5/2}} \left( \frac{3\mu_0 I_0 \sqrt{A/\pi}r(t)}{2(A/\pi + r(t)^2)^{5/2}} \right) = \frac{9\mu_0^2 I_0^2 r(t)^2 v(t) A^2 \pi^4}{4R(A+ \pi r(t)^2)^{5}} .\]
This is just the force due to a single current ring on the permanent magnet. To find the total force on the permanent magnet, one must integrate in both directions of \(r(t)\) above and below the permanent magnet. Keeping in mind that the force above is just a magnitude and that the function for the force is even, it suffices to compute the force due to one direction and double it:
\[ \begin{align} F_{\text{total}} &=2 \int_0^{\infty} \frac{9\mu_0^2 I_0^2 r(t)^2 v(t) A^2 \pi^4}{4R(A+ \pi r(t)^2)^{5}} dr =\frac{9\mu_0^2 I_0^2 v(t) A^2 \pi^4}{2R} \int_0^{\infty} \frac{r(t)^2}{(A+ \pi r(t)^2)^{5}} dr \\ &= \frac{9\mu_0^2 I_0^2 v(t) A^2 \pi^4}{2R} \left(\frac{5}{256 \sqrt{\pi} A^{7/2}} \right) = \frac{45\mu_0^2 I_0^2\pi^{3/2}}{512 R A^{3/2}} v(t) \end{align} \]
The form of the force is a viscous damping force proportional to the velocity, which is a good check of the validity of the above discussion.
Finally, writing down Newton's second law will allow the velocity to be found. The magnet is accelerated by gravity, which is opposed by the magnetic force written above:
\[Mv'(t) = Mg - \frac{45\mu_0^2 I_0^2\pi^{3/2}}{512 R A^{3/2}} v(t).\]
Define the constant, dependent on the parameters \(I_0\), \(R\), and \(A\):
\[\kappa = \frac{45\mu_0^2 I_0^2\pi^{3/2}}{512 R A^{3/2}}.\]
Then Newton's second law reads:
\[Mv'(t) = Mg - \kappa v(t).\]
This first order ODE, with the initial condition \(v(0) = 0\) because the permanent magnet is dropped from rest, is solved by:
\[v(t) = \frac{Mg}{\kappa} \left(1- e^{-\frac{\kappa t}{M}}\right) = \frac{512 Mg R A^{3/2}}{45\mu_0^2 I_0^2\pi^{3/2}} \left(1- e^{-\frac{\kappa t}{M}}\right) .\]
At late times, the permanent magnet approaches a terminal velocity \(\frac{Mg}{\kappa}\) exponentially quickly. Furthermore, if the permanent magnet is weak (\(\kappa \approx 0\)) the RHS above can be Taylor expanded:
\[v(t) \approx \frac{Mg}{\kappa} \left(\frac{\kappa t}{M} - \frac{\kappa^2 t^2}{2M^2} \right) = gt - \frac{\kappa g t^2}{2M} .\]
This provides a small negative correction at early times to the usual linear growth \(gt\) of the velocity, as expected.
Many approximations have been made throughout this computation: the approximation of the magnetic dipole as a current loop, the approximation that the tube is long and the cross-section small so that edge effects are insignificant, and the assumption that the interaction of the magnet with each current ring can be modeled by the dipole-dipole interaction well. Nevertheless, the analytic expression obtained above captures the qualitative behavior of the physical scenario very well. If the cross-section of the tube is wide or the resistance high, the induced current is small and the damping is very slow with a higher terminal velocity. If \(I_0\) is large, the permanent magnet is very strong, inducing a strong damping effect, consistent with the small terminal velocity and high speed of damping found above.
The same effect is visible in MRI scanners, which are like tubes that have much more powerful magnetic fields. Below, Lenz's law is demonstrated in the slow motion of an aluminum bar in the magnetic field of an MRI:
![The powerful magnetic field of an MRI induces a magnetic field from the aluminum bar that causes a force acting against gravity. The bar is falling <em>in real time</em> [3].](https://d18l82el6cdm1i.cloudfront.net/uploads/3Pr2BJDnfX-mri.gif) The powerful magnetic field of an MRI induces a magnetic field from the aluminum bar that causes a force acting against gravity. The bar is falling in real time [3].
The powerful magnetic field of an MRI induces a magnetic field from the aluminum bar that causes a force acting against gravity. The bar is falling in real time [3].
Compare the speeds at which a permanent magnet and a piece of metal of the same shape and mass fall through a conducting tube.
The permanent magnet will:
References
[1] Purcell, E.M. Electricity and Magnetism. Third Edition. Cambridge University Press, 2013.
[2] Excerpted from https://www.youtube.com/watch?v=keMpUaoA3Tg using GIPHY.com.
[3] Excerpted from https://www.youtube.com/watch?v=liDjr439-fY using GIPHY.com.