Ampere's Law
One of Maxwell's equations, Ampère's law, relates the curl of the magnetic field to the current density and is particularly useful for current distributions with high degrees of symmetry.
Motivation
The Biot-Savart law requires summing many infinitesimal current elements and thus allows for the direct calculation of any configuration of magnetic field due to current-carrying wires. As with Coulomb's law in electrostatics, this type of sum can get quite complicated.
Analogous to electrostatics, in which Gauss's law allows for the convenient calculation of the electric field of systems with symmetry, in magnetostatics Ampère's law can be used to readily determine the magnetic field of symmetric systems of current elements.
Recall that the motivation for Gauss's law (in its integral form) makes a statement of the relationship between regional charge distribution and the electric field summed over a surface (in the form of electric flux). Likewise, when considering paths of current elements, one might consider the magnetic field over an entire path. \((\)In magnetostatics, it intuitively makes sense to consider paths (and not surfaces as with electrostatics), as one is concerned with current-carrying paths.\()\)
Just as the electric flux is computed over a Gaussian surface, with an alternative statement of the Biot-Savart law, one might aspire to sum the magnetic field over a closed directed path, or a so-called Amperian loop. And, similarly, instead of considering the total charge contained inside a Gaussian surface, here one considers the total current enclosed by an Amperian loop. As with a Gaussian surface, with an Amperian loop there is an orientation to the loop. In general, one defines the positive orientation of the loop as the counterclockwise direction. This convention can be remembered by curling the fingers on one's right hand around one's thumb (the so-called "right-hand rule").
To see how this might be related to current-carrying elements, consider the Amperian loops shown below, which are of different sizes. A single current-carrying wire (pointing out of the page) passes through each figure, as shown.
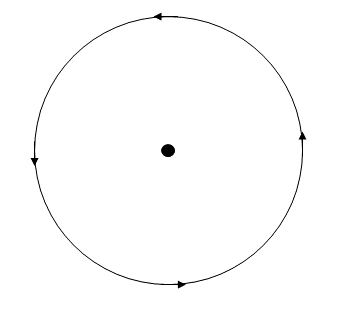

Consider the sum of the magnetic field over the top two loops. In particular, let the component of the magnetic field tangent to each point on the loops be summed continuously over each field, which is represented by the integral
\[ \int_\text{loop} \mathbf{B} \cdot d\mathbf{s}, \]
which is a so-called line integral. In a great many cases \((\)such as constant \( \mathbf{B} \cdot d\mathbf{s}),\) the integral will not have to be computed directly from the definition. Instead, symmetry arguments may suffice to obtain the value of the integral.
In the first loop, the path itself is quite small, but the magnetic field is strong close to the wire. In the large loop below it, the path is much larger, but the magnetic field is much weaker. Indeed, by the Biot-Savart law, one knows that the field weakens by exactly a factor \( 1/r \), where \( r \) is the radius of the loop. Thus, the linear change in the size of a circular loop is exactly balanced out by the decrease in the strength of the magnetic field at the location of the loop. In other words, the sum of the magnetic field over the direction of a circular loop is
\[ 2 \pi r \frac{\mu_0 I}{2 \pi r} = \mu_0 I, \]
which is independent of \( r \). Thus, it is not unreasonable to consider that perhaps the physical dimensions of a loop does not matter so much as the current \( I \) contained with the loop. If a loop is farther away from a current source, then its path is longer, but the corresponding field strength decreases proportionally with the increase in path length.
One might also consider the following Amperian loop:
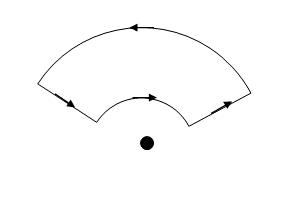
The field through the two circular arc segments cancel by the previous reasoning. Along one of the arcs, the sum of the field over the loop is some fraction of \( \mu_0 I \), while along the other the sum must be the exact opposite (but same magnitude) due to the reversed direction of the path. Furthermore, along the radially oriented segments, the sum of the field must be zero because all of the components of the field are perpendicular to the radial direction. Thus, the sum of the field of the loop is zero. In this case, no current passes through the interior of the loop, and no net magnetic field arises when summed over the loop. A similar argument could be made for any general loop that does not contain any current elements.
Indeed, by drawing an analogy with Gauss's law, one might conjecture the following:
- The integral of the magnetic field over an Amperian loop is independent of the geometry or size of the loop.
- The integral depends only on the current contained within the loop. In particular, the integral is proportional to the current contained inside the loop. (Furthermore, based on the calculation for the circular loops, the constant of proportionality must be \( \mu_0 \).)
- As a corollary, the integral is zero when no current passes through the interior of the loop.
Ampère's Law
The integral form of Ampère's law can be stated as follows. It can be shown to be equivalent to the Biot-Savart law.
Ampère's law (integral form):
Given a counterclockwise-oriented closed loop (Amperian loop) inside which a total current \( I_\text{encl} \) is enclosed,
\[ \int_{\text{loop}} \mathbf{B} \cdot d\mathbf{s} = \mu_0 I_\text{encl}. \]
As with Gauss's law, which can be used to calculate the total charge distribution from the field or vice versa, Ampère's law can be used to determine the field or enclosed current in situations with some symmetry. A clever choice of Amperian loop is often needed to exploit the symmetry of a given system.
Note that care must be taken to orient the loop correctly with respect to the direction of the current. With the loop oriented counterclockwise in the page, all currents passing out of the page are positive, while those going into the page are negative.
Field of a current-carrying wire:
To calculate the magnetic field from a current-carrying wire of current \( I \), we choose a circular Amperian loop of radius \( r \) centered at the wire. Because \( \mathbf{B} \cdot d\mathbf{s} \) is constant, it follows that
\[ B (2\pi r) = \mu_0 I \implies B = \frac{\mu_0 I}{2\pi r}, \]
where \( B \) is the magnitude of the field.
Field of a solenoid:
Suppose that one has a cylindrical solenoid, a coil of wire wrapped around a cylindrical core. A side view of the solenoid is as shown below. If the solenoid (measured along its axis) is long compared to its radius, then the field inside the solenoid near the middle is very nearly constant due to symmetry.

We choose a rectangular Amperian loop such that the one side of the loop is on the interior of the solenoid and one sits outside. The side outside of the loop can be chosen to be sufficiently far away from the solenoid such that it feels a negligible field.
The field integrated over the two sides of the loop perpendicular to the axis of the solenoid must come out to zero, for both sides feel the same field at all corresponding points along their paths but in opposite orientations. If the length of the side of path inside the solenoid is \( L \), then F gives
\[ B L = \mu_0 N I, \]
where \( N \) is the number of turns of wire over the length \( L \). Instead, writing \( n = N/L \) as the density of turns (in number of turns per unit length), one has
\[ B = \mu_0 n I. \]
In other words, the field strength depends only on the current and density of turns, not the total number.
If both sides of the Amperian loop parallel to the axis are instead chosen to reside outside of the solenoid, then instead Ampère's law gives
\[ B L = 0, \]
so there is zero field outside of the solenoid.
Field inside a thick wire:
A thick wire of outer radius \( R \) carries steady current distributed uniformly over the wire. What is the field inside and outside of the wire if the total current is \( I?\)
Once again, we choose a circular Amperian loop of radius \( r \) centered at the axis of the wire.
Outside the wire \( (r > R), \) Ampère's law gives the same result as for a standard thin wire, or
\[ B = \frac{\mu_0 I}{2\pi r}. \]
Inside the wire \( (r \leq R), \) the total current enclosed is \( I\big(r^2/R^2\big) \), so Ampère's law gives
\[ B(2\pi r) = \mu_0 I (r^2/R^2) \implies B = \frac{\mu_0 I r}{2\pi R^2}. \]
Since the total current increases quadratically with \( r \) while the decay of the field (for the current elements inside the loop) occurs proportionally to \( 1/r \), the field as a whole increases linearly with \( r \).
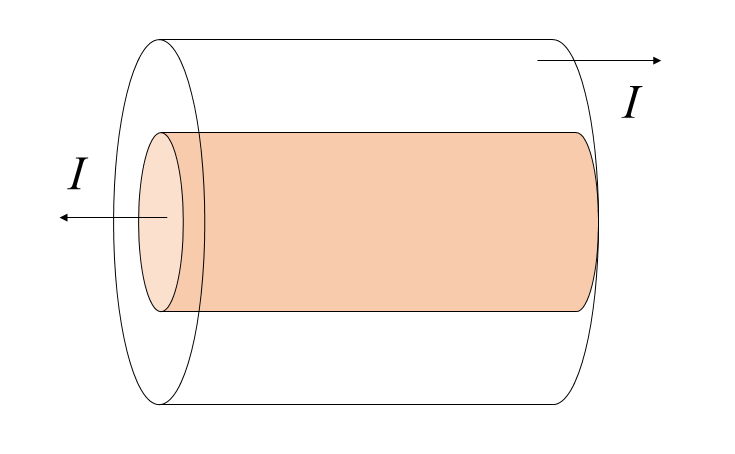
A coaxial cable consists of an inner solid cylindrical wire of radius \( 2 \, \text{mm} \) and an outer conducting hollow cylinder of radius \( 4 \, \text{mm} \), which each carry a current of magnitude \( 100 \, \text{mA} \). If the currents travel in opposite directions, what is the magnitude of the magnetic field outside of the cable a distance of \( 1 \, \text{cm} \) measured perpendicularly from the central axis of the inner wire?

The number of turns of the two solenoids are the same.
Differential Form
To express Ampère's law in a local form, one can use Stokes' theorem to rewrite the line integral \( \int \mathbf{B} \cdot d\mathbf{s} \) in terms of the surface integral of the curl of \( \mathbf{B} \):
\[ \int_\text{loop} \mathbf{B} \cdot d\mathbf{s} = \int_\text{surface} \nabla \times \mathbf{B} \cdot d\mathbf{a}. \]
But Ampère's law says that
\[ \int_\text{loop} \mathbf{B} \cdot d\mathbf{s} = \mu_0 I_\text{encl} = \mu_0 \int_\text{surface} \mathbf{J} \cdot d\mathbf{a}, \]
where \( \mathbf{J} \) is the current density. It is the generalized, continuous version of the current \( I \). Of course, the surface integral in both equations can be taken over any chosen closed surface, so the integrands must be equal:
\[ \nabla \times \mathbf{B} = \mu_0 \mathbf{J}. \]
This is the so-called differential form of Ampère's law, as it expresses Ampère's law in terms of a differential operator, the curl.
Maxwell's Modification
In what is one of the great triumphs of physics, perhaps the most brilliant between the eras of Newton and Einstein, in the mid-nineteenth century Maxwell showed that the "naive" form of Ampère's law that has been used is necessarily inadequate, or at the very least, not fully generalized. As it turns out, analogous to Faraday's law, in which a time-varying magnetic field leads to an electric field, a time-varying electric field also leads to a magnetic field. In other words, a positive curl in the magnetic field can be the result not only of steady currents but also of time-varying electric fields.
Maxwell added a term called the displacement current to represent the contribution of the time-varying electric field to \( \nabla \times \mathbf{B} \). The size of the additional term, he reasoned, must be \( \epsilon_0 \partial \mathbf{E}/\partial t \). In that case, Ampère's law reads
\[ \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}. \]
This is the full form of Ampère's law, complete with Maxwell's modifications. Sometimes it is called the Ampère-Maxwell law, although most of the time it is simply referred to as "Ampère's law" proper. Usually, it is clear when \( \frac{\partial \mathbf{E}}{\partial t}\) is relevant in a given problem, so there is no ambiguity about whether one is referring to the naive or modified form of Ampère's law.
To be sure, in practice the size of the additional term \( \mu_0 \epsilon_0 \partial \mathbf{E}/\partial t \) is sufficiently small so as to be ignored. To see why, note that the speed of an electromagnetic wave is
\[ c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}, \]
so one can also write
\[ \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \frac{1}{c^2} \frac{\partial \mathbf{E}}{\partial t}. \]
In general, \( \partial \mathbf{E}/\partial t \) is much smaller than \( c^2 \), so the term is not easily measured experimentally.
The importance of Maxwell's additional term lies in the fact that it allows one to do the following. For simplicity suppose there is some region of space in which the electric field \( E(x) \) is non-zero only along the \( z \)-axis and the magnetic field \( B(x) \) is non-zero only along the \( y \)-axis, such that both are functions of \( x \) only. Then Faraday's law gives
\[ \frac{\partial E}{\partial x} = -\frac{\partial B}{\partial t}. \]
Even though \( \mathbf{J} = 0 \), with the additional term, Ampere's law now gives
\[ \frac{\partial B}{\partial x} = -\frac{1}{c^2} \frac{\partial E}{\partial t}. \]
Taking the partial derivative of the first equation with respect to \( x \) and the second with respect to \( t \) yields
\[\begin{align} \frac{\partial^2 E}{\partial x^2} &= -\frac{\partial^2 B}{\partial x \partial t} \\ \frac{\partial^2 B}{\partial t \partial x} &= -\frac{1}{c^2} \frac{\partial^2 E}{\partial t^2}. \end{align} \]
Therefore,
\[ \frac{\partial^2 E}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 E}{\partial t^2}. \]
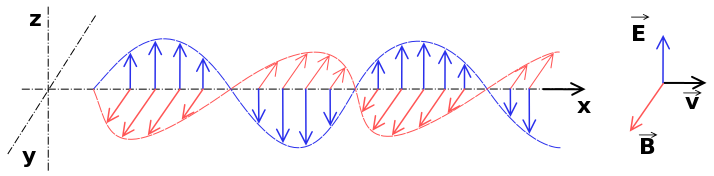
This equation has solutions for \( E(x) \) \(\big(\)and corresponding solutions for \( B(x)\big) \) that represent traveling electromagnetic waves. In fact, the equation that has just been derived is in fact in the same form as the classical wave equation in one dimension. In other words, the laws of electricity and magnetism permit for the electric and magnetic fields to travel as waves, but only if Maxwell's displacement current term is added to Ampère's law. Indeed, Maxwell was the first to provide a theoretical explanation of a classical electromagnetic wave and, in doing so, compute the speed of light.
(The general solution consists of linear combinations of sinusoidal components, as shown below.)
References
[1] Griffiths, D.J. Introduction to Electrodynamics. Fourth edition. Pearson, 2014.
[2] Purcell, E.M. Electricity and Magnetism. Third edition. Cambridge University Press, 2013.