Magnetic Moment
If placed at an angle in a magnetic field, a current loop will experience torque and rotate. The propensity of a current distribution to experience torque in a magnetic field (and also create its own magnetic field) is characterized by its magnetic (dipole) moment.
In electrostatics, electric charge can exist as single (monopole) charges. However, there is no such equivalent in magnetostatics. According to Gauss's law for magnetism, there are no monopole sources of magnetic field. Since there is no magnetic charge, magnetic moment turns out to be a quantity of fundamental importance in describing magnetic phenomena and materials.
Indeed, the magnetization of matter is defined in terms of the dipole moment per unit volume. But fundamental particles, such as the electron and proton, can also carry intrinsic magnetic moment in the form of spin. The fact that particles have spin has profound consequences. In chemistry, for instance, a correct description of spin is needed to obtain a correct description of atomic energies and the bonding of the chemical elements.
Contents
Definition
Consider a square current loop of side length \( l \) placed at some angle \( \phi \) with respect to a uniform magnetic field of magnitude \( B \) as shown below. If some current \( I \) flows counterclockwise in the loop, each segment will feel some force, but there will be no net force on the loop. Rather, the forces on opposite ends of the loop cancel, and there will be no net translation of the center of the loop.
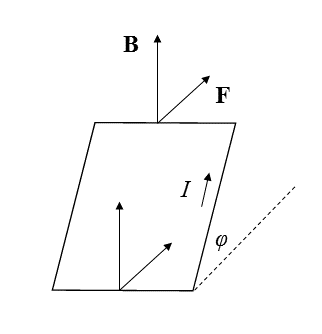
However, there is a torque on the loop. The force on each segment is of magnitude \( I l B \). Two sides of the loop \((\)with no \( F \) labeled in the diagram\()\) contribute no torque, as the force on them lies entirely within the plane of the loop.
The other two sides contribute some nonzero component \( I l B \sin{\phi} \) perpendicular to the loop. Thus, relative to the center of the loop, each segment contributes torque \( I l^2 B \sin{\phi} / 2 \), with the total given by \( I s^2 B \sin{\phi} \). Thus, if the magnetic field is held fixed, the size of the torque on the loop depends only on its area \( s^2 \) and the current \( I \).
A similar argument could be made for a current loop of any geometry. One would find that the torque depends only on the product of \( I \) and the area \( a \). Thus, to characterize how strongly a magnetic field will rotate a given current loop, it makes sense to define the magnetic (dipole) moment of the loop as
\[ \mathbf{m} = I \mathbf{a}. \]
Note that the magnetic dipole moment has been defined as a vector quantity (with the area vector \( a \) defined via the same convention as with electric and magnetic flux) so that instead of writing the torque as \( \mu B \sin{\phi} \), one can simply use the compact vector notation
\[ \mathbf{\tau} = \mathbf{m} \times \mathbf{B}. \]
Consider a simple classical model for a hydrogen atom. Suppose an electron \((\)of charge \( -e \) and mass \( m_e) \) orbits the nucleus \((\)of charge \( + e \) and mass \( M \gg m_e) \) and is confined purely by electrostatic forces to a circular orbit of radius \( R \). What is the magnetic moment of the electron?
The electrostatic attraction of the nucleus provides the entirety of the centripetal force keeping the electron in place. Therefore, the speed \( v \) of the electron is determined by
\[ \frac{m_e v^2}{R} = \frac{1}{4\pi \epsilon_0} \frac{e^2}{R^2}, \]
which implies
\[ v^2 = \frac{1}{4\pi\epsilon_0} \frac{e^2}{R m_e}. \]
To determine the magnetic moment, first note that the period of the electron's motion is \( 2 \pi R / v \). Thus, the current is \( -e / (2 \pi R / v ) = - ev / (2\pi R) \), and the corresponding magnetic moment is
\[ m = -\frac{evR}{2} = - \frac{e^2}{2} \sqrt{\frac{R}{4\pi\epsilon_0 m_e}}. \]
Substituting values for \( e \), \( R \), and \( m_e \) yields \( m = 9.27 \times 10^{-24} \, \text{A} \cdot \text{m}^2 \). (N.B. Keep in mind the fact that the electron is so small; the magnetic moment per mass is rather considerable.)
Find the magnetic moment of circular disk of radius \( R \) and uniform surface charge density \( \sigma \) that rotates at angular velocity \( \omega \).
We divide the disk into many small rings of width \( dr \). The current produced by the ring is the total charge contained divided by the period for one rotation. Thus
\[ dI = \frac{\sigma(2\pi r \, dr)}{\omega/(2\pi)}. \]
Factoring in the area of each ring gives
\[\begin{align} dm &= \big(\pi r^2\big) \frac{\sigma(2\pi r dr)}{\omega/(2\pi)} \\&= \sigma \omega \pi r^3 \, dr \\\\ m &= \int_0^R \sigma \omega \pi r^3 \, dr \\&= \frac{1}{4} \sigma \omega \pi R^4. \end{align}\]
A cylindrical solenoid of length \( 10 \, \text{cm} \) and cross-sectional area \( 9 \, \text{cm}^2 \) makes \( 800 \) turns per meter with a current of \( 50 \, \text{mA} \) flowing through it. If the solenoid is placed in a magnetic field of magnitude \( 0.5 \, \text{mT} \) such that the long axis of the solenoid is perpendicular to the field, determine the total torque on the solenoid in \( \text{N} \cdot \text{m} \).
Force on a Magnetic Dipole
While it is true that a magnetic dipole experiences no net force in a uniform magnetic field, the force is not necessarily zero in a spatially varying magnetic field. It turns out that the force is related to the gradient of the field:
\[ \mathbf{F} = \nabla(\mathbf{m} \cdot \mathbf{B}), \]
in analogy with the similar expression for the force on an electric dipole.
Field of a Magnetic Dipole
Describing the field of a current loop (off of the perpendicular axis through the loop's center) can prove, as direct calculations with the Biot-Savart law show. A neater approach is to use the magnetic vector potential. The general result is
\[ \mathbf{A}_\text{dipole}(\mathbf{r}) = \frac{\mu_0 I}{4\pi r^2} \frac{\mathbf{m} \times \hat{\mathbf{r}}}{r^2}, \]
where \( \hat{\mathbf{r}} \) is directed from the loop to the point in question.
Suppose the loop is oriented such that the perpendicular axis points along the \( z \)-axis. By taking the components of \( \nabla \times \mathbf{A} \), one can show that the field is
\[\begin{align} B_x &= \frac{\mu_0}{4\pi} \frac{3 m \sin{\theta}\cos{\theta}}{r^3} \\ B_z &=- \frac{\mu_0}{4\pi} \frac{m(3\cos^2{\theta} - 1)}{r^3}. \end{align}\]
Note that these expressions are analogous to those of an electric dipole. The magnetic field can also be written in the form
\[ \mathbf{B}(\mathbf{r}) = \frac{\mu_0}{4\pi r^3} [3 (\mathbf{m} \cdot \hat{\mathbf{r}})\hat{\mathbf{r}} - \mathbf{m}]. \]
Given a circular wire loop of radius \( 5 \, \text{cm} \) that carries current \( 500 \, \text{mA} \), let \( B \) be the magnitude of the magnetic field a distance of \(5 \, \text{m} \) from the center of the loop as measured along an axis perpendicular to the plane of the loop that goes through the center of the loop. (Assume that the radius of the loop is much smaller than the distance along the axis.)
Find \( B / \mu_0 \) in \( \text{A}/\text{m} \).
Multipole Expansion
Actually, considering only magnetic dipoles is necessarily an approximation, as a current loop produces a "pure" dipole field only in the limit of small loop area. In reality, for a macroscopic current distribution, there will be additional terms in the expression for the magnetic field.
The multipole expansion of the vector potential in terms of Legendre polynomials yields
\[\mathbf{A}(\mathbf{r}) = \frac{\mu_0 I}{4\pi} \sum_{n=0}^\infty \frac{1}{r^{n+1}} \int r'^n P_n(\cos{\theta}')\, d\mathbf{l}',\]
where \( P_n \) denotes the \( n \)th Legendre polynomial. The first few terms of the sum are
\[\begin{align} \mathbf{A}_\text{monopole}(\mathbf{r}) &= \frac{\mu_0 I}{4\pi} \frac{1}{r} \int d \mathbf{l}' \\&= 0 \\\\ \mathbf{A}_\text{dipole}(\mathbf{r}) &= \frac{\mu_0 I}{4\pi} \frac{1}{r^2} \int r' \cos{\theta'} d \mathbf{l}' \\\\ \mathbf{A}_\text{quadrupole}(\mathbf{r}) &= \frac{\mu_0 I}{4\pi} \frac{1}{r^3} \int \frac{r'^2}{2} \left( 3\cos^2{\theta'} - 1 \right) d \mathbf{l}'. \end{align}\]
Appropriately, the so-called monopole term vanishes, and Gauss's law for magnetism is satisfied.
Clearly, the magnetic dipole term reappears in the multipole expansion, but additional terms (quadrupole, octupole, etc.) appear. To show that the dipole term is consistent with the previous discussion, one can rewrite the cosine term as a dot product:
\[ \mathbf{A}_\text{dipole}(\mathbf{r}) = \frac{\mu_0 I}{4\pi} \frac{1}{r^2} \int \big(\mathbf{r}' \cdot \hat{\mathbf{r}}\big)\, d \mathbf{l}'. \]
One can show that the integral evaluates to \( -\hat{\mathbf{r}} \times \mathbf{a} \), in which case the dipole term becomes
\[ \mathbf{A}_\text{dipole}(\mathbf{r}) = \frac{\mu_0 I}{4\pi r^2} \frac{\mathbf{m} \times \hat{\mathbf{r}}}{r^2}, \]
where \( \mathbf{m} = I \mathbf{a} \) is simply the magnetic dipole moment defined previously. The remaining terms all represent higher-order contributions to the field. In many practical situations, if non-vanishing, the dipole term tends to dominate over all others, and the higher moments may be ignored.
References
[1] Griffiths, D.J. Introduction to Electrodynamics. Fourth edition. Pearson, 2014.
[2] Purcell, E.M. Electricity and Magnetism. Third edition. Cambridge University Press, 2013.