Pascal's Triangle
Pascal's triangle is a triangular array constructed by summing adjacent elements in preceding rows. Pascal's triangle contains the values of the binomial coefficient. It is named after the \(17^\text{th}\) century French mathematician, Blaise Pascal (1623 - 1662).
\[1\\ 1\quad 1\\ 1\quad 2 \quad 1\\ 1\quad 3 \quad 3 \quad 1\\ 1\quad 4 \quad 6 \quad 4 \quad 1\\ 1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1\\ \cdots\]
Pascal's triangle can be used to visualize many properties of the binomial coefficient and the binomial theorem.
Contents
Construction of Pascal's Triangle
Begin by placing a \(1\) at the top center of a piece of paper. The next row down of the triangle is constructed by summing adjacent elements in the previous row. Because there is nothing next to the \(1\) in the top row, the adjacent elements are considered to be \(0:\)

This process is repeated to produce each subsequent row:


This can be repeated indefinitely; Pascal's triangle has an infinite number of rows:

Notation of Pascal's Triangle
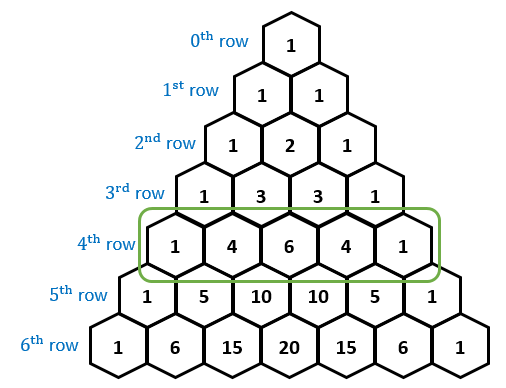
The topmost row in Pascal's triangle is considered to be the \(0^\text{th}\) row. The next row down is the \(1^\text{st}\) row, then the \(2^\text{nd}\) row, and so on. The leftmost element in each row is considered to be the \(0^\text{th}\) element in that row. Then, to the right of that element is the \(1^\text{st}\) element in that row, then the \(2^\text{nd}\) element in that row, and so on.

With this convention, each \(i^\text{th}\) row in Pascal's triangle contains \(i+1\) elements.
The convention of beginning the order with \(0\) may seem strange, but this is done so that the elements in the array correspond to the values of the binomial coefficient.
Let \(x_{i,j}\) be the \(j^\text{th}\) element in the \(i^\text{th}\) row of Pascal's triangle, with \(0\le j\le i\). Then,
\[x_{i,j}=\binom{i}{j}.\]
This property of Pascal's triangle is a consequence of how it is constructed and the following identity:
Let \(n\) and \(k\) be integers such that \(1\le k\le n\). Then,
\[\binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k}.\]
Using Pascal's triangle, what is \(\binom{6}{2}\)?
Look for the \(2^\text{nd}\) element in the \(6^\text{th}\) row. The value of that element will be \(\binom{6}{2}\).

Thus, \(\binom{6}{2}=15\). \(_\square\)
\[\begin{array}{rc} 0^\text{th} \text{ row:} & 1 \\ 1^\text{st} \text{ row:} & 1 \quad 1 \\ 2^\text{nd} \text{ row:} & 1 \quad 2 \quad 1 \\ 3^\text{rd} \text{ row:} & 1 \quad 3 \quad 3 \quad 1 \\ 4^\text{th} \text{ row:} & 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ \vdots \ \ \ & \cdot \quad \cdot \quad \cdot \quad \cdot \quad \cdot \quad \cdot \end{array} \]
Pascal's triangle is shown above for the \(0^\text{th}\) row through the \(4^\text{th}\) row. What is the \(4^\text{th}\) element in the \(10^\text{th}\) row?
\(\)
Note: Each row starts with the \(0^\text{th}\) element. For example, the \(0^\text{th}\), \(1^\text{st}\), \(2^\text{nd}\), and \(3^\text{rd}\) elements of the \(3^\text{rd}\) row are 1, 3, 3, and 1, respectively.
Patterns in Pascal's Triangle
Pascal's triangle is a way to visualize many patterns involving the binomial coefficient. Here are some of the ways this can be done:
The \(n^\text{th}\) row of Pascal's triangle contains the coefficients of the expanded polynomial \((x+y)^n\).
Expand \((x+y)^4\) using Pascal's triangle.
The \(4^\text{th}\) row will contain the coefficients of the expanded polynomial.
\[(x+y)^4=\color{blue}{1}x^4+\color{blue}{4}x^3y+\color{blue}{6}x^2y^2+\color{blue}{4}xy^3+\color{blue}{1}y^4\]
Start at any of the "\(1\)" elements on the left or right side of Pascal's triangle. Sum elements diagonally in a straight line, and stop at any time. Then, the next element down diagonally in the opposite direction will equal that sum.
If you start at the \(r^\text{th}\) row and end on the \(n^\text{th}\) row, this sum is
\[\sum\limits_{k=r}^{n}\binom{k}{r}=\binom{n+1}{r+1}.\]
Using Pascal's triangle, what is \(\displaystyle\sum\limits_{k=2}^{5}\binom{k}{2}?\)
Start at a \(1\) on the \(2^\text{nd}\) row, and sum elements diagonally in a straight line until the \(5^\text{th}\) row:

\[1+3+6+10=20.\]
Or, simply look at the next element down diagonally in the opposite direction, which is \(20\). \(_\square\)
\[ \begin{array}{c} 1 \end{array} \\ \begin{array}{cc} 1 & 1 \end{array} \\ \begin{array}{ccc} 1 & 2 & \color{red}{1}\end{array} \\ \begin{array}{cccc} 1 & 3 & \color{red}{3} & 1\end{array} \\ \begin{array}{ccccc} 1 & 4 & \color{red}{6} & 4 & 1\end{array} \\ \begin{array}{cccccc} \vdots & \hphantom{\vdots} & \vdots & \hphantom{\vdots} & \vdots \end{array}\\ \begin{array}{cccccc} 1 & 25 & \color{red}{300} & 2300 & 12650 & \cdots \end{array} \\ \begin{array}{ccccccc} 1 & 26 & 325 & 2600 & 14950 & \cdots & \hphantom{1000} \end{array} \\ \]
Pascal's triangle is shown above for the \(0^\text{th}\) row through the \(4^\text{th}\) row, and parts of the \(25^\text{th}\) and \(26^\text{th}\) rows are also shown above.
What is the sum of all the \(2^\text{nd}\) elements of each row up to the \(25^\text{th}\) row?
\(\)
Note: The visible elements to be summed are highlighted in red.
Additional clarification: The topmost row in Pascal's triangle is the \(0^\text{th}\) row. Then, the next row down is the \(1^\text{st}\) row, and so on. The leftmost element in each row of Pascal's triangle is the \(0^\text{th}\) element. Then, the element to the right of that is the \(1^\text{st}\) element in that row, and so on.
The sum of the elements in the \(n^\text{th}\) row of Pascal's triangle is equal to \(2^n\).
This is a way to express the identity
\[\sum\limits_{k=0}^{n}\binom{n}{k}=2^n.\]
\[ \begin{array}{c} 1 \end{array} \\ \begin{array}{cc} 1 & 1 \end{array} \\ \begin{array}{ccc} 1 & 2 & 1 \end{array} \\ \begin{array}{cccc} 1 & 3 & 3 & 1\end{array} \\ \begin{array}{ccccc} 1 & 4 & 6 & 4 & 1\end{array} \\ \begin{array}{cccccc} \vdots & \hphantom{\vdots} & \vdots & \hphantom{\vdots} & \vdots \end{array} \\ \]
Pascal's triangle is shown above for the \(0^\text{th}\) row through the \(4^\text{th}\) row.
What is the sum of all the elements in the \(12^\text{th}\) row?
\(\)
Note: The topmost row in Pascal's triangle is the \(0^\text{th}\) row. Then, the next row down is the \(1^\text{st}\) row, and so on.
The following property follows directly from the hockey stick identity above:
The \(2^\text{nd}\) element in the \((n+1)^\text{th}\) row is the \(n^\text{th}\) triangular number.
This is a way to express the identity
\[\sum\limits_{k=1}^{n}{k}=\binom{n+1}{2}.\]
Construct a Pascal's triangle, and shade in even elements and odd elements with different colors. The shading will be in the same pattern as the Sierpinski Gasket:

This is an application of Lucas's theorem.