SAT Right Triangles

To successfully solve problems about right triangles on the SAT, you need to know:

all triangles on the SAT are non-degenerate
how to classify triangles by angles and sides
that the measures of the angles in a triangle add to \(180^\circ\)
the Pythagorean Theorem

Pythagorean Theorem

In a right triangle, the square of the hypotenuse equals the sum of the square of the legs.

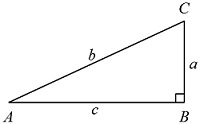
\[b^2 = a^2 + c^2\]

how to determine if a triangle is right, acute, or obtuse, given the lengths of its sides

If \(c^2 = a^2 + b^2,\) then \(m\angle C = 90\) and \(\triangle ABC\) is right.

If \(c^2 < a^2 + b^2,\) then \(m\angle C < 90\) and \(\triangle ABC\) is acute.

If \(c^2 > a^2 + b^2,\) then \(m\angle C > 90\) and \(\triangle ABC\) is obtuse.

the relationship between the sides of the special right triangles

\(30^\circ-60^\circ-90^\circ\) Triangle
In a \(30^\circ-60^\circ-90^\circ\) triangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is \(\sqrt{3}\) times as long as the shorter leg.

\(45^\circ-45^\circ-90^\circ\) Triangle
In a \(45^\circ-45^\circ-90^\circ\) triangle, the hypotenuse is \(\sqrt{2}\) times longer than either of the legs.

Pythagorean Theorem

If the perimeter of a square is 16, which of the following is the length of its diagonal?

(A) \(\ \ 2\sqrt{2}\)
(B) \(\ \ 4\)
(C) \(\ \ 4\sqrt{2}\)
(D) \(\ \ 8\sqrt{2}\)
(E) \(\ \ 16\sqrt{2}\)

Correct Answer: C

Solution:

Tip: Draw a picture.
Tip: Perimeter of a polygon equals the sum of the lengths of its sides.
Tip: Pythagorean Theorem: \(a^2 + b^2 = c^2.\)
A square \(ABCD\) has four sides of equal length. Its perimeter in terms of one of its sides, \(\overline{AB}\), is

\[\begin{align} 4\cdot AB &= P\\ 4\cdot AB &= 16\\ AB &= 4 \end{align}\]

This is shown in the picture below.

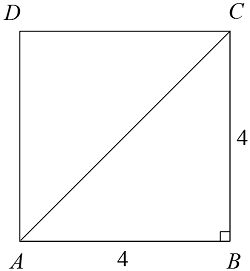
\(\triangle ABC\) is a right triangle whose hypotenuse is the diagonal of the square. To find the length of the hypotenuse, we use the Pythagorean Theorem:

\[\begin{align} 4^2 + 4^2 &= AC^2\\ 16 + 16 &= AC^2\\ 32 &= AC^2\\ \sqrt{32} &= AC\\ 4\sqrt{2} &= AC\\ \end{align}\]

Note that since the length of a segment is a positive number, when square rooting we select the positive root.

Incorrect Choices:

(A)
If you calculate half the length of the diagonal, you will get this wrong answer.

(B)
Tip: The simplest choice may not be the correct one.
This is the length of the side of the square, not the length of its diagonal.

(D)
If you calculate the sum of the lengths of both diagonals, you will get this wrong answer.

(E)
Tip: Read the entire question carefully.
If you think the side of the square equals 16, you will get this wrong answer. The perimeter of the square is equal to 16, and one of its sides equals 4.

Special Right Triangles

In the figure above, every triangle is a \(30^\circ-60^\circ-90^\circ\) triangle and, for each pair of triangles, the hypotenuse of the triangle to the right is twice as long as the long leg of the triangle to the left. If the short leg of the smallest triangle is \(\sqrt{3},\) what is the value of \(a?\)

(A) \(\ \ 3\sqrt{3}\)
(B) \(\ \ 9\)
(C) \(\ \ 8\sqrt{3}\)
(D) \(\ \ 9\sqrt{3}\)
(E) \(\ \ 18\)

Correct Answer: B

Note:

In both solutions, we will refer to the smallest triangle as the 1st \(\triangle\), and working our way clockwise, we will refer to the biggest triangle as the 4th \(\triangle.\)

If you understand the relationship between the triangles and their sides, this problem can be done very quickly, like this:

\[a=\text{short leg of 1st}\ \triangle \cdot \sqrt{3} \cdot \sqrt{3} \cdot \sqrt{3} = \sqrt{3} \cdot \sqrt{3} \cdot \sqrt{3} \cdot \sqrt{3} = 9.\]

Solution 1 arrives at this result by applying the properties of \(30^\circ - 60^\circ - 90^\circ\) triangles for each triangle; Solution 2 explains it using similar triangles.

Solution 1:

Tip: Know the \(30^\circ-60^\circ-90^\circ\) and the \(45^\circ-45^\circ-90^\circ\) Triangles.
We are told that the short leg of the 1st \(\triangle = \sqrt{3}.\) In a \(30^\circ-60^\circ-90^\circ\) triangle, the longer leg is \(\sqrt{3}\) times the shorter leg. Therefore,

\[\text{long leg of 1st}\ \triangle = \sqrt{3} \cdot \sqrt{3} = 3.\]

We are also given that the hypotenuse of each successive triangle is twice the long leg of the triangle with which it overlaps. So,

\[\text{hypotenuse of 2nd}\ \triangle = 2 \cdot \text{long leg of 1st}\ \triangle = 2 \cdot 3 = 6.\]

By the properties of \(30^\circ-60^\circ-90^\circ\) triangles,

\[\text{long leg of 2nd}\ \triangle = \frac{\sqrt{3}}{2} \cdot \text{hypotenuse of 2nd}\ \triangle = \frac{\sqrt{3}}{2} \cdot 6 = 3\sqrt{3}.\]

We apply the given again, this time to the 3rd \(\triangle:\)

\[\text{hypotenuse of 3rd}\ \triangle = 2 \cdot \text{long leg of 2nd}\ \triangle = 2 \cdot 3\sqrt{3} = 6\sqrt{3}\]

and by the properties of \(30^\circ-60^\circ-90^\circ\) triangles:

\[\text{long leg of 3rd}\ \triangle = \frac{\sqrt{3}}{2} \text{hypotenuse of 3rd}\ \triangle = \frac{\sqrt{3}}{2} \cdot 6\sqrt{3} = 9.\]

We apply the given to the 4th \(\triangle:\)

\[\text{hypotenuse of 4th}\ \triangle = 2 \cdot \text{long leg of 3rd}\ \triangle = 2 \cdot 9 = 18\]

and by the \(30^\circ-60^\circ-90^\circ\) Theorem:

\[a=\text{short leg of 1st}\ \triangle = \frac{\text{hypotenuse of 2nd}\ \triangle}{2} = \frac{18}{2} = 9.\]

Solution 2:

Tip: Know the \(30^\circ-60^\circ-90^\circ\) and the \(45^\circ-45^\circ-90^\circ\) Triangles.
Tip: AA Postulate: Two triangles are similar if two angles of one triangle are congruent to two angles of the other triangle.
We are told that the short leg of the 1st \(\triangle = \sqrt{3}.\) In a \(30^\circ-60^\circ-90^\circ\) triangle, the longer leg is \(\sqrt{3}\) times the shorter leg. Therefore,

\[\text{long leg of 1st}\ \triangle = \sqrt{3} \cdot \sqrt{3} = 3.\]

We are also told that the hypotenuse of each successive triangle is twice the long leg of the triangle with which it overlaps. So,

\[\text{hypotenuse of 2nd}\ \triangle = 2 \cdot \text{long leg of 1st}\ \triangle = 2 \cdot 3 = 6.\]

Applying the properties of \(30^\circ-60^\circ-90^\circ\) triangles to the 2nd \(\triangle\),

\[\text{short leg of 2nd}\ \triangle = \frac{\text{hypotenuse of 2nd}\ \triangle}{2} = \frac{6}{2} = 3.\]

By the AA Similarity Postulate, the 2nd \(\triangle\) is similar to the 1st \(\triangle,\) and the factor of proportionality is

\[\frac{\text{short leg of 2nd}\ \triangle}{\text{short leg of 1st}\ \triangle} = \frac{3}{\sqrt{3}}.\]

In fact, by the AA Similarity Postulate, all four triangles are similar. And because the relationship between the sides of each successive pair of triangles is the same, the factor of proportionality between the 3rd and 2nd triangles, and between the 4th and 3rd triangles is also \(\frac{3}{\sqrt{3}}.\) So,

\[\frac{\text{short leg of 3rd}\ \triangle}{\text{short leg of 2nd}\ \triangle} = \frac{3}{\sqrt{3}}\]

\[\text{short leg of 3rd}\ \triangle = \frac{3}{\sqrt{3}} \cdot \text{short leg of 2nd}\ \triangle\]

\[\text{short leg of 3rd}\ \triangle = \frac{3}{\sqrt{3}} \cdot 3 = \frac{9}{\sqrt{3}}\]

and

\[\frac{\text{short leg of 4th}\ \triangle}{\text{short leg of 3rd}\ \triangle} = \frac{3}{\sqrt{3}}\]

\[\text{short leg of 4th}\ \triangle = \frac{3}{\sqrt{3}} \cdot \text{short leg of 3rd}\ \triangle\]

\[a = \text{short leg of 4th}\ \triangle = \frac{3}{\sqrt{3}} \cdot \frac{9}{\sqrt{3}} = 9\]

(A)
Tip: Read diagrams carefully.
If you miscount the number of triangles -- if you stop at the third triangle -- you will get this wrong answer.

(C)
Starting with the smallest triangle, if you think each successive short leg is twice as long as the short leg of the previous triangle, you will get this wrong answer.

(D)
Tip: Read diagrams carefully.
If you count one too many triangles, you will get this wrong answer.

(E)
Tip: Read the entire question carefully.
If you find the hypotenuse of the biggest triangle, instead of \(a,\) you will get this wrong answer.

Review

If you thought these examples difficult and you need to review the material, these links will help:

SAT Tips for Right Triangles

Pythagorean Theorem: \(a^2 + b^2 = c^2.\)

If \(c^2 = a^2 + b^2,\) then \(m\angle C = 90\) and \(\triangle ABC\) is right.

If \(c^2 < a^2 + b^2,\) then \(m\angle C < 90\) and \(\triangle ABC\) is acute.

If \(c^2 > a^2 + b^2,\) then \(m\angle C > 90\) and \(\triangle ABC\) is obtuse.

Know the \(30^\circ-60^\circ-90^\circ\) and the \(45^\circ-45^\circ-90^\circ\) Theorems.

AA Postulate: Two triangles are similar if two angles of one triangle are congruent to two angles of the other triangle.

The measures of the angles in a triangle add to \(180^\circ.\)

Perimeter of a polygon equals the sum of the lengths of its sides.

SAT General Tips

Pythagorean Theorem

Contents