Skip List

The skip list is a probabilisitc data structure that is built upon the general idea of a linked list. The skip list uses probability to build subsequent layers of linked lists upon an original linked list. Each additional layer of links contains fewer elements, but no new elements.

You can think about the skip list like a subway system. There's one train that stops at every single stop. However, there is also an express train. This train doesn't visit any unique stops, but it will stop at fewer stops. This makes the express train an attractive option if you know where it stops.

Skip lists are very useful when you need to be able to concurrently access your data structure. Imagine a red-black tree, an implementation of the binary search tree. If you insert a new node into the red-black tree, you might have to rebalance the entire thing, and you won't be able to access your data while this is going on. In a skip list, if you have to insert a new node, only the adjacent nodes will be affected, so you can still access large part of your data while this is happening.

A skip list starts with a basic, ordered, linked list. This list is sorted, but we can't do a binary search on it because it is a linked list and we cannot index into it. But the ordering will come in handy later.

Then, another layer is added on top of the bottom list. This new layer will include any given element from the previous layer with probability \(p.\) This probability can vary, but oftentimes \(\frac12\) is used. Additionally, the first node in the linked list is often always kept, as a header for the new layer. Take a look at the following graphics and see how some elements are kept but others are discarded. Here, it just so happened that half of the elements are kept in each new layer, but it could be more or less--it's all probabilistic. In all cases, each new layer is still ordered.

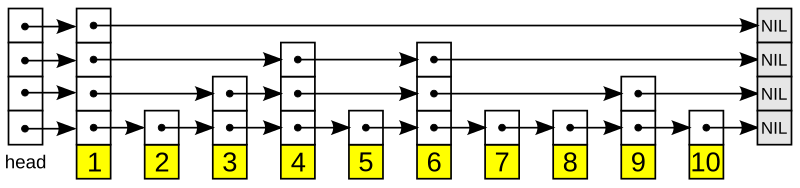An example implementation of a skip list ^[1]

A skip list \(S\) has a few important properties that are referenced in its analysis. It has a height of \(h\) which is the number of linked lists in it. It has a number of distinct elements, \(n.\) And it has a probability \(p,\) which is usually \(\frac12.\)

The highest element (one that appears in the most lists) will appear in \(\log_\frac{1}{p}(n)\) lists, on average--we'll prove this later. This, if we use \(p = \frac12\), there are \(\log_2(n)\) lists. This is the average value of \(h\). Another way of saying "Every element in a linked list is in the linked list below it" is "Every element in level \(S_{i+1}\) exists in level \(S_i.\)"

Each element in the skip list has four pointers. It points to the node to its left, its right, its top, and its bottom. These quad-nodes will allow us to efficiently search through the skip list.

Time

The complexity of a skip list is complicated due to its probabilistic nature. We will prove its time complexity below, but for now we will just look at the results. It is important to note, though, that these bounds are expected or average-case bounds. This is because we use randomization in this data structure:

\[\begin{array} &&\text{Insertion - O}\big(\log(n)\big), &\text{Deletion - O}\big(\log(n)\big), \\ &\text{Indexing - O}\big(\log(n)\big), &\text{Search - O}\big(\log(n)\big).\end{array}\]

The worst-case bounds for the skip list are below, but we won't worry about these for analysis:

\[\begin{array} &&\text{Insertion - O}(n), &\text{Deletion - O}(n), \\ &\text{Indexing - O}(n), &\text{Search - O}(n).\end{array}\]

Space

Space is a little easier to reason about. Suppose we have the total number of positions in our skip list equal to

\[n \sum_{i=0}^{h} \frac{1}{2^i}.\]

That is equal to

\[n \cdot \left(1+\frac12 + \frac14 + \frac18+\cdots\right) = n \cdot 2\]

because of the infinite summation. Therefore, our expected space utilization is simply

\[\begin{array} &&\text{Space - O}(n). \end{array}\]

This is also not concrete. Probabilistically, our skip list could grow much higher. However, this is the expected space complexity.

There are four main operations in the skip list.

Search

The input to this function is a search key, key. The output of this function is a position, p, such that the value at this position is the largest that is less than or equal to key.

1
2
3
4
5
6
7

Search(key)
    p = top-left node in S
    while (p.below != null) do        //Scan down
        p = p.below
        while (key >= p.next) do      //Scan forward
            p = p.next
    return p

Essentially, we are scanning down the skip list, then scanning forward.

Indexing

This functions in the exact same way as Search, so we will omit the code.

Insertion

The input for insertion is a key. The output is the topmost position, p, at which the input is inserted. Note that we are using the Search method from above. We use a function called CoinFlip() that mimics a fair coin and returns either heads or tails. Finally, the function insertAfter(a, b) simply inserts the node a after the node b.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

Insert(key)
    p = Search(key)
    q = null
    i = 1
    repeat
        i = i + 1                   //Height of tower for new element
        if i >= h
            h = h + 1
            createNewLevel()        //Creates new linked list level
        while (p.above == null)
            p = p.prev              //Scan backwards until you can go up
        p = p.above
        q = insertAfter(key, p)     //Insert our key after position p
    until CoinFlip() == 'Tails'
    n = n + 1
    return q

First, we always insert the key into the bottom list at the correct location. Then, we have to promote the new element. We do so by flipping a fair coin. If it comes up heads, we promote the new element. By flipping this fair coin, we are essentially deciding how big to make the tower for the new element. We scan backwards from our position until we can go up, and then we go up a level and insert our key right after our current position.

While we are flipping our coin, if the number of heads starts to grow larger than our current height, we have to make sure to create new levels in our skip list to accommodate this. Lines 7-9 of this function take care of that for us.

Deletion

Deletion takes advantage of the Search operation and is simpler than the Insertion operation. We will save space by writing the pseudocode more verbosely.

1
2
3
4
5
6

Delete(key)
    Search for all positions p_0, ..., p_i where key exists
    if none are found
        return
    Delete all positions p_0, ..., p_i
    Remove all empty layers of skip list

Delete can be implemented in many ways. Since we know when we find our first instance of key, it will be connected to all others instances of key, and we can easily delete them all at once.

Earlier, we said that there will be \(\log_2(n)\) lists in total. But why? If each newly created level is done so probabilistically, how can we know that?

The probability \(P_i\) that an element in skip list \(S\) with \(n\) total elements gets up to level \(i\) is just

\[P_i = \frac1{2^i} \]

because if the probability is \(\frac12,\) then to create a new level, we're tossing a coin for each element to see if it should be included. So, the probability that at least one of the \(n\) elements gets to level \(i\) is

\[P_i \le \frac{n}{2^i}.\]

Let's try some numbers to see what this means. If \(i = \log_2(n),\) then

\[P_i \le \frac{n}{2^{\log_2(n)}} = 1.\]

If \(i\) increases slightly to \(i = 3 \cdot \log_2(n)\), then

\[P_i \le \frac{n}{2^{3\log_2(n)}} = \frac1{n^2}.\]

This means, that if \(n = 1000 \), there is one in a million chance of any one particular element making it to the top layer. This analysis, of course, is not strict, but with a high probability (a word used often in randomized algorithms), \(S\) has a height of \(\log_2(n)\).

As we discussed earlier, the worst-case scenario for skip lists is quite bad. In fact, the height of the skip list can stretch towards \(\infty\) because we are using random coin flips. However, this analysis is not fair because skip lists perform much better on average. Let's take the operation Search. This is the main focus of the skip list because both Insertion and Deletion are proved the same way.

Search

There are two nested while loops in this function. There is the outer loop that is akin to "scanning down" the skip list, and there is the inner loop which is like "scanning forward" in the skip list.

We have proven above that the height \(h\) of the skip list is \(O\big(\log_2(n)\big).\) So, the maximum number of moves down the skip list we can make is \(O\big(\log_2(n)\big).\)

Now, let's bound the number of scans forward we can make. Let's say we scanned \(n_i\) keys at level \(i\) before we dropped down to level \(i-1\). Each subsequent key that we scan after we drop into this level cannot exist in level \(i\), or otherwise we would have already seen it. The probability that any given key in this level is in level \(i\) is \(\frac12.\) That means the expected number of keys we will be encountering in our new level once we've dropped down is 2, a \(O(1)\) operation.

So, our two steps of scanning down and scanning forward take \(O\big(\log_2(n)\big)\) and \(O(1)\) time, respectively. That means our total time for search is \(O\big(\log_2(n)\big).\)

If this analysis feels similar to binary search trees, that's because it is! If you look closely at the skip list, it resembles a tree, with lower levels larger than higher levels.

1. Mula, W. Wikipedia Skip Lists. Retrieved April 20, 2016, from https://en.wikipedia.org/wiki/Skip_list