Incenter

The incenter of a triangle is the center of its inscribed circle. It has several important properties and relations with other parts of the triangle, including its circumcenter, orthocenter, area, and more.

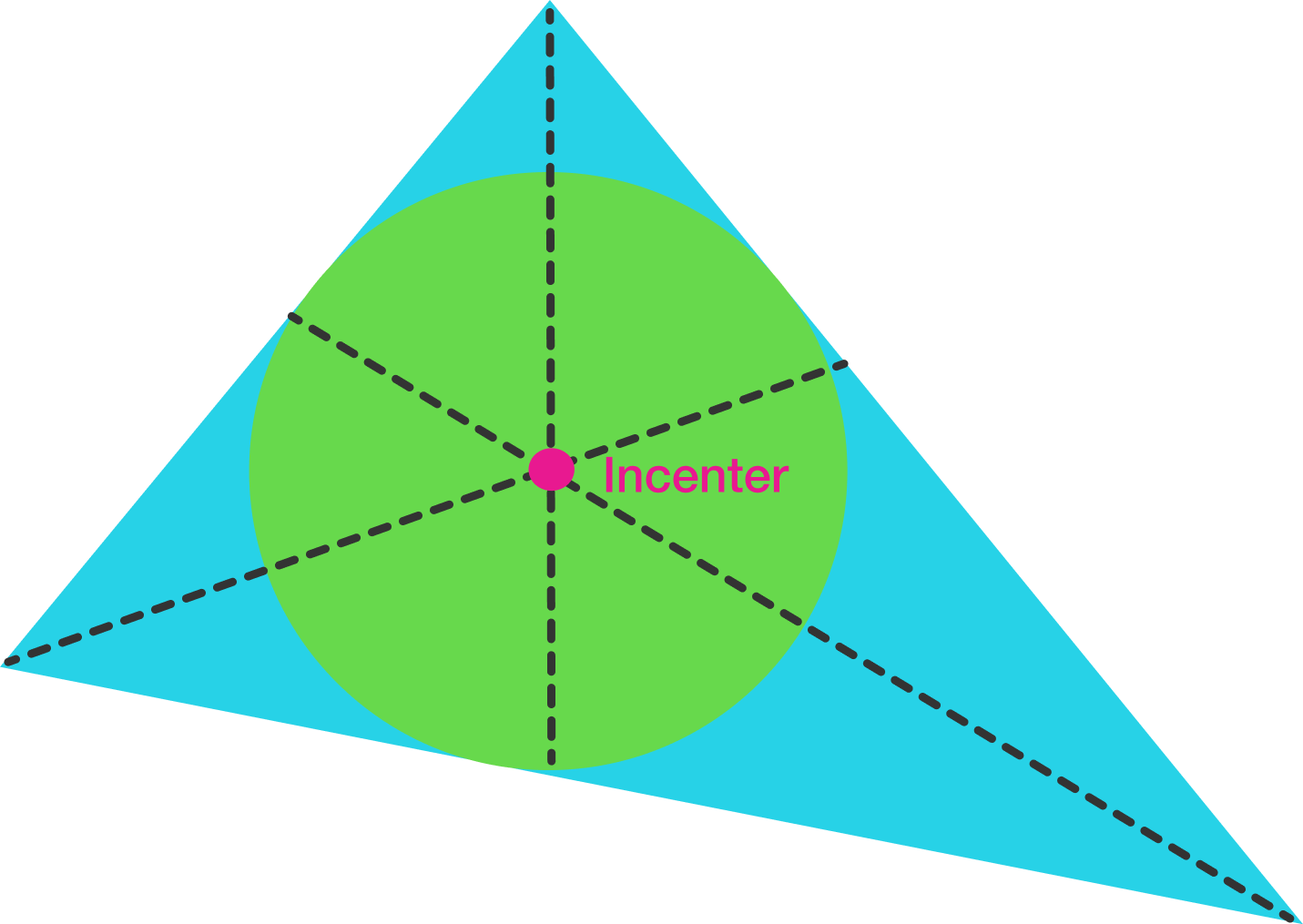
The incenter is typically represented by the letter $I$.

All triangles have an incenter, and it always lies inside the triangle. One way to find the incenter makes use of the property that the incenter is the intersection of the three angle bisectors, using coordinate geometry to determine the incenter's location. Unfortunately, this is often computationally tedious.

Generally, the easiest way to find the incenter is by first determining the inradius, or radius of the incircle, usually denoted by the letter $r$ (the letter $R$ is reserved for the circumradius). This can be done in a number of ways, detailed in the 'Basic properties' section below. Once the inradius is known, each side of the triangle can be translated by the length of the inradius, and the intersection of the resulting three lines will be the incenter. This, again, can be done using coordinate geometry.

Alternatively, the following formula can be used. For a triangle with side lengths $a,b,c$, with vertices at the points $(x_1, y_1), (x_2, y_2), (x_3, y_3)$, the incenter lies at

$$\left(\dfrac{ax_1+bx_2+cx_3}{a+b+c}, \dfrac{ay_1+by_2+cy_3}{a+b+c}\right).$$

A triangle has vertices at $A=(0,0), B=(14,0)$, and $C=(5,12)$. What are the coordinates of the incenter?

---

The lengths of the sides (using the distance formula) are $$a=\sqrt{(14-5)^2+(12-0)^2}=15, b=\sqrt{(5-0)^2+(12-0)^2}=13, c=\sqrt{(14-0)^2+(0-0)^2}=14.$$ Now the above formula can be used: $$I = \left(\dfrac{15 \cdot 0+13 \cdot 14+14 \cdot 5}{13+14+15}, \dfrac{15 \cdot 0+13 \cdot 0+14 \cdot 12}{13+14+15}\right)=\left(6, 4\right).\ _\square$$

The simplest proof is a consequence of the trigonometric version of Ceva's theorem, which states that $AD, BE, CF$ concur if and only if

$$\frac{\sin\angle BAD}{\sin\angle ABE} \cdot \frac{\sin \angle CBE}{\sin \angle BCF} \cdot \frac{\sin\angle ACF}{\sin \angle CAD} = 1.$$

In this case, $D,E,F$ are the feet of the angle bisectors, so $\angle BAD=\angle CAD$, $\angle ABE=\angle CBE$, and $\angle ACF=\angle BCF$. As a result,

$$\frac{\sin\angle BAD}{\sin\angle CAD} \cdot \frac{\sin\angle ABE}{\sin\angle CBE} \cdot \frac{\sin\angle ACF}{\sin\angle BCF} = 1 \cdot 1 \cdot 1 = 1$$

and rearranging the left hand side gives

$$\frac{\sin\angle BAD}{\sin\angle ABE} \cdot \frac{\sin \angle CBE}{\sin \angle BCF} \cdot \frac{\sin\angle ACF}{\sin \angle CAD} = 1.$$

Therefore, the three angle bisectors intersect at a single point, $I$.

Furthermore, since $I$ lies on the angle bisector of $\angle BAC$, the distance from $I$ to $AB$ is equal to the distance from $I$ to $AC$. Similarly, this is also equal to the distance from $I$ to $BC$. Therefore, $I$ is the center of the inscribed circle, proving the existence of the incenter.

An alternate proof involves the length version of Ceva's theorem and the angle bisector theorem.

It's been noted above that the incenter is the intersection of the three angle bisectors.

For a triangle with semiperimeter (half the perimeter) $s$ and inradius $r$,

The area of the triangle is equal to $sr$.

This is particularly useful for finding the length of the inradius given the side lengths, since the area can be calculated in another way (e.g. Heron's formula), and the semiperimeter is easily calculable.

As a corollary,

In a right triangle with integer side lengths, the inradius is always an integer.

If $D$ is the point where the incircle touches $BC$, and similarly $E,F$ are where the incircle touches $AC$ and $AB$ respectively, then $AE=AF=s-a, BD=BF=s-b, CD=CE=s-c$. As a corollary,

$AE+BF+CD=s$, and also $r = \sqrt{\dfrac{AE \cdot BF \cdot CD}{AE+BF+CD}}.$

Furthermore $AD, BE,$ and $CF$ intersect at a single point, called the Gergonne point.

If the altitudes of a triangle have lengths $h_1, h_2, h_3$, then

$$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\dfrac{1}{h_3}=\dfrac{1}{r}.$$

Let the sides of the triangle be $a,b,c$. Then, since $\frac{1}{2} a h_1= \Delta$, and similarly for other sides, $\sum \frac{1}{h_1} = \sum \frac{a}{2 \Delta} = \frac{2s}{2 \Delta} = \frac{1}{ \Delta/s}= \frac{1}{r}.$

The incircle and circumcircle are also intimately related. According to Euler's theorem,

$$(R-r)^2 = d^2+r^2,$$

where $R$ is the circumradius, $r$ the inradius, and $d$ the distance between the incenter and the circumcenter. Equivalently, $d=\sqrt{R(R-2r)}$. This also proves Euler's inequality: $R \geq 2r$. Equality holds only for equilateral triangles.

Additionally,

$$rR=\frac{abc}{2(a+b+c)}, ~\text{ and }~ IA \cdot IB \cdot IC = 4Rr^2.$$

Incircles also relate well with themselves. If $r_1, r_2, r_3$ are the radii of the three circles tangent to the incircle and two sides of the triangle, then

$$r=\sqrt{r_1r_2}+\sqrt{r_2r_3}+\sqrt{r_3r_1}.$$

On a different note, if the circumcircle of $ABC$ is drawn, and $M$ is the midpoint of minor arc $BC$, then

$M$ is also the circumcenter of $\triangle BIC$.

Equivalently, $MB=MI=MC$. This is known as "Fact 5" in the Olympiad community.

Similarly, if point $E$ lies on the circumcircle of $BCI$ so that $BC=EC$, then $\angle BCE=\angle BAC$. $EC$ is also perpendicular to $CO$, where $O$ is the circumcenter of $ABC$.

All triangles have an incircle, and thus an incenter, but not all other polygons do. When one exists, the polygon is called tangential. As in a triangle, the incenter (if it exists) is the intersection of the polygon's angle bisectors.

In the case of quadrilaterals, an incircle exists if and only if the sum of the lengths of opposite sides are equal: Both pairs of opposite sides sum to $a+b+c+d$

• Circumcenter
• Orthocenter
• Centroid