Bearing - Word Problems

Most bearing word problems involving trigonometry and angles can be reduced to finding relationships between angles and the measurements of the sides of a triangle. In this case, finding the right basic trigonometric functions to relate the angles and measurements are crucial for setting up and solving the problem correctly.

Trigonometry of angles and sides can be used on a daily basis in the workplace like in carpentry, construction work, engineering, etc.

Before jumping to the word problems, here are the basic definitions you need to be familiar with:

The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (also known as the line of sight).

The angle of elevation in the above diagram is $\alpha^\circ$.

If the object is below the level of the observer, then the angle between the horizontal and the observer's line of sight is called the angle of depression.

The angle of depression in the above diagram is $\beta^\circ$.

It is often useful to draw a diagram and remember how the basic trigonometric functions relate the angles and measurements of sides in a right triangle. Finding the right trigonometric function to relate the angles and measurements is crucial to solving the problems. We will demonstrate the principle of setting up and solving trigonometric word problems by working through several examples.

A surveyor in a helicopter at an elevation of 1000 meters measures the angle of depression to the far edge of an island as $24^\circ$ and the angle of depression to the near edge as $31^\circ$. How wide is the island, to the nearest meter?

---

Let the horizontal distance between the helicopter and the island be $d$, and the width of the island $w$. Then $\tan 24^\circ = \frac{1000}{d+w}$ and $\tan 31^\circ = \frac{1000}{d}$, implying $d = \frac{1000}{\tan 31^\circ}$. Substituting this into $\tan 24^\circ = \frac{1000}{d+w}$ gives

$$\begin{aligned} \tan 24^\circ &= \frac{1000}{\frac{1000}{\tan 31^\circ}+w} \\ \tan 24^\circ \left(\frac{1000}{\tan 31^\circ}+w \right) &= 1000 \\ w &= \frac{1000\left( 1 - \frac{\tan 24^\circ}{ \tan 31^\circ }\right)}{\tan 24^\circ} \\\\ & \approx 581.75 . \end{aligned}$$

Thus, the width of the island is 582 meters

Alternatively, you can calculate the difference between $\cot 24^\circ$ and $\cot 31^\circ$ (which is 0.581757292) and multiply it by 1000 meters. $_\square$

Andrew was flying a kite on a hill, but he dumped his kite into the pond below. If the length of the string of his kite is 150 meters and the angle of depression from his position to the kite is $30^\circ$, then how high is the hill where he is standing?

---

Let's first draw a diagram for a better understanding of the problem:

So it is a right triangle with base angle $30^\circ$, hypotenuse 150 meters, and the side $h$ opposite to the given angle being the same as the height of the hill. We use the sine ratio to find the height:

$$\begin{aligned} \sin 30^\circ&=\dfrac{h}{150} \\ \dfrac 12 &=\dfrac{h}{150} \\ \\ \Rightarrow h&=75 \text{ (m)}. \end{aligned}$$

Hence the hill is 75 meters above the lake. $_\square$

The angle of elevation of the top of an incomplete vertical pillar at a horizontal distance of 100 meters from its base is 45 degrees. If the angle of elevation of the top of the complete pillar from the same spot is to be 60 degrees, then by how much the height of the incomplete pillar should be increased?

---

Let's draw a diagram to figure out the situation:

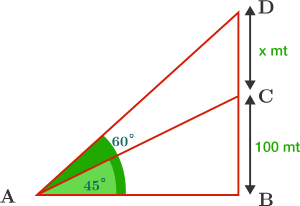
Let $BC$ be the height of the incomplete pillar, and $BD$ the height of the complete pillar. We are given that $BC=100\text{ m}, \angle BAC = 45^\circ,$ and $\angle BAD = 60^\circ$. And we assume that the length of $CD$ is $x$ meters.

In triangle $ABC$, we know that

$$\begin{aligned} \tan 45^\circ & =\frac{BC}{AB} \\\\ AB & =BC \\ & =100 \text{ m}.\end{aligned}$$

Similarly, in triangle $ABD$, we know that

$$\begin{aligned} \tan 60^\circ & =\frac{BD}{AB} \\ \sqrt 3 & = \frac{BD}{100} \\\\ \Rightarrow BD & =100 \sqrt 3 \text{ m}.\end{aligned}$$

And from the above figure,

$$\begin{aligned} BD&=BC+CD \\ 100\sqrt3 &=100+x \\\\ \Rightarrow x&=100 \big( \sqrt3 -1 \big) \text{ m}. \end{aligned}$$

Hence the height of the incomplete pillar is to be increased by $100 \big( \sqrt3 -1 \big) \text{ m}$ to complete the pillar. $_\square$

Jim and Ted live on one side of the river, and Martha lives on the other side. The distance across the river is 100 yards. Ted, who lives downstream from Matha, measures an angle of 35 degrees between the shoreline and a straight line leading to Martha's house. Jim, who lives upstream from Martha, measures an angle of 60 degrees. How far apart do Ted and Jim live?

---

First off, a picture will help (to get your "bearing"--no pun intended).

The relative positions of Martha, Jim, and Ted are represented in this picture:

Now, it is much easier to visualize what is going on. The distance in yards from Jim to the position directly across the stream from Matha is given as

$$\tan 60^\circ = \frac{100}{x}.$$

And the distance in yards from Jim to the position directly across the stream from Matha is given as

$$\tan 35^\circ = \frac{100}{y}.$$

So, the distance from Ted to Jim is given by

$$\begin{aligned} \text{Distance} &= x + y \\ &= \frac{100}{\tan 60^\circ} + \frac{100}{\tan 35^\circ}\\\\ &= 57.7 + 142.8 \\ &= 200.5 \text{ (yards)}.\ _\square \end{aligned}$$

A private plane flies for 1.3 hours at 110 mph on a bearing of 40°. Then it turns and continues another 1.5 hours at the same speed, but on a bearing of 130°. At the end of this time, how far is the plane from its starting point?

---

The bearings tell us the angles from "due north" in a clockwise direction. Since 130 – 40 = 90, the two bearings give us a right triangle. From the times and rates, we have

$$\begin{aligned} 1.3 × 110 &= 143\\ 1.5 × 110 &= 165. \end{aligned}$$

Now, let's give the geometrical shape to our problem and set up a triangle:

Using the Pythagorean theorem, we get

\[\begin{align} m^2 & =143^2 + 165^2 \\
& =20449 + 27225 \\ & =47674 \\\\ \Rightarrow m & = 218.34. \end{align} \]

Hence the plane is approximately 218 miles away at the end of the time. $_\square$

Try the following bearing word problems:

This section is meant to enhance the problem-solving skills of bearing word problems. Here an example is illustrated followed by some problems for you to attempt:

A six-meter-long ladder leans against a building. If the ladder makes an angle of $60^\circ$ with the ground,

(1) how far up the wall does the ladder reach, and
(2) how far from the wall is the base of the ladder?

---

To understand the situation, let's draw a diagram:

• (1) From the above diagram, we get the following equation to obtain the value of $h:$ $$\begin{aligned} \sin 60^\circ & =\dfrac h6 \\ \Rightarrow h & =6 \times \sin 60^\circ \\ & =3 \sqrt 3. \end{aligned}$$ So the ladder can reach $3\sqrt3$ meters up the wall. $$$$

• (2) Similarly, we can get the value of $b$ as follows: $$\begin{aligned} \cos 60^\circ &=\dfrac b6 \\ \Rightarrow b&=6 \times \cos 60^\circ \\ &=3. \end{aligned}$$ Hence the base of the ladder is 3 meters from the wall. $_\square$

Here are the problems to gain a strong grab over the bearing concept:

• Lengths in Right Triangles

• Sine Rule

• Trigonometric Equations