Feedforward Neural Networks
 A feedforward neural network with information flowing left to right
A feedforward neural network with information flowing left to right
Feedforward neural networks are artificial neural networks where the connections between units do not form a cycle. Feedforward neural networks were the first type of artificial neural network invented and are simpler than their counterpart, recurrent neural networks. They are called feedforward because information only travels forward in the network (no loops), first through the input nodes, then through the hidden nodes (if present), and finally through the output nodes.
Feedfoward neural networks are primarily used for supervised learning in cases where the data to be learned is neither sequential nor time-dependent. That is, feedforward neural networks compute a function \(f\) on fixed size input \(x\) such that \(f(x) \approx y\) for training pairs \((x, y)\). On the other hand, recurrent neural networks learn sequential data, computing \(g\) on variable length input \(X_k = \{x_1, \dots, x_k\}\) such that \(g(X_k) \approx y_k\) for training pairs \((X_n, Y_n)\) for all \(1 \le k \le n\).
Singe-layer Perceptron
The simplest type of feedforward neural network is the perceptron, a feedforward neural network with no hidden units. Thus, a perceptron has only an input layer and an output layer. The output units are computed directly from the sum of the product of their weights with the corresponding input units, plus some bias.
Historically, the perceptron's output has been binary, meaning it outputs a value of \(0\) or \(1\). This is achieved by passing the aforementioned product sum into the step function \(H(x)\). This is defined as
\(H(x) = \begin{cases} 1 && \mbox{if }\ x \ge 0 \\ 0 && \mbox{if }\ x \lt 0. \end{cases}\)
For a binary perceptron with \(n\)-dimensional input \(\vec{x}\), \(n\)-dimensional weight vector \(\vec{w}\), and bias \(b\), the \(1\)-dimensional output \(o\) is
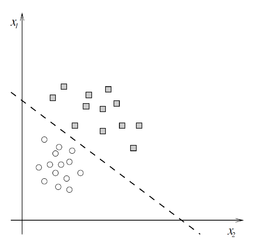 A linear classifier, where squares evaluate to 1 and circles to 0
A linear classifier, where squares evaluate to 1 and circles to 0
\(o = \begin{cases} 1 && \mbox{if }\ \vec{w} \cdot \vec{x} + b \ge 0 \\ 0 && \mbox{if }\ \vec{w} \cdot \vec{x} + b \lt 0. \end{cases}\)
Since the perceptron divides the input space into two classes, \(0\) and \(1\), depending on the values of \(\vec{w}\) and \(b,\) it is known as a linear classifier. The diagram to the right displays one such linear classifier. The line separating the two classes is known as the classification boundary or decision boundary. In the case of a two-dimensional input (as in the diagram) it is a line, while in higher dimensions this boundary is a hyperplane. The weight vector \(\vec{w}\) defines the slope of the classification boundary while the bias \(b\) defines the intercept.
More general single-layer peceptrons can use activation functions other than the step function \(H(x)\). Typical choices are the identity function \(f(x) = x,\) the sigmoid function \(\sigma(x) = \left(1 + e^{-x}\right)^{-1},\) and the hyperbolic tangent \(\tanh (x) = \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}}.\) Use of any of these functions ensures the output is a continuous number (as opposed to binary), and thus not every activation function yields a linear classifier.
Generally speaking, a perceptron with activation function \(g(x)\) has output
\[o = g(\vec{w} \cdot \vec{x} + b).\]
In order for a perceptron to learn to correctly classify a set of input-output pairs \((\vec{x}, y)\), it has to adjust the weights \(\vec{w}\) and bias \(b\) in order to learn a good classification boundary. The figure below shows many possible classification boundaries, the best of which is the boundary labeled \(H_2\). If the perceptron uses an activation function other than the step function (e.g. the sigmoid function), then the weights and bias should be adjusted so that the output \(o\) is close to the true label \(y\).
 An example of binary classified data and multiple classification boundaries
An example of binary classified data and multiple classification boundaries
Error Function
Typically, the learning process requires the definition of an error function \(E\) that quantifies the difference between the computed output of the perceptron \(o\) and the true value \(y\) for an input \(\vec{x}\) over a set of multiple input-output pairs \((\vec{x}, y)\). Historically, this error function is the mean squared error (MSE), defined for a set of \(N\) input-output pairs \(X = \{(\vec{x_1}, y_1), \dots, (\vec{x_N}, y_N)\}\) as
\[E(X) = \frac{1}{2N} \sum_{i=1}^N \left(o_i - y_i\right)^2 = \frac{1}{2N} \sum_{i=1}^N \left(g(\vec{w} \cdot \vec{x_i} + b) - y_i\right)^2,\]
where \(o_i\) denotes the output of the perceptron on input \(\vec{x_i}\) with activation function \(g\). The factor of \(\frac{1}{2}\) is included in order to simplify the calculation of the derivative later. Thus, \(E(X) = 0\) when \(o_i = y_i\) for all input-output pairs \((\vec{x_i}, y_i)\) in \(X\), so a natural objective is to attempt to change \(\vec{w}\) and \(b\) such that \(E(X)\) is as close to zero as possible. Thus, minimizing \(E(X)\) with respect to \(\vec{w}\) and \(b\) should yield a good classification boundary.
Delta Rule
\(E(X)\) is typically minimized using gradient descent, meaning the perceptron adjusts \(\vec{w}\) and \(b\) in the direction of the negative gradient of the error function. Gradient descent works for any error function, not just the mean squared error. This iterative process reduces the value of the error function until it converges on a value, usually a local minimum. The values of \(\vec{w}\) and \(b\) are typically set randomly and then updated using gradient descent. If the random initializations of \(\vec{w}\) and \(b\) are denoted \(\vec{w_0}\) and \(b_0\), respectively, then gradient descent updates \(\vec{w}\) and \(b\) according to the equations
\[\vec{w_{i+1}} = \vec{w_i } - \alpha \frac{\partial E(X)}{\partial \vec{w_i}}\\ b_{i+1} = b_i - \alpha \frac{\partial E(X)}{\partial b_i},\]
where \(\vec{w_i}\) and \(b_i\) are the values of \(\vec{w}\) and \(b\) after the \(i^\text{th}\) iteration of gradient descent, and \(\frac{\partial f}{\partial x}\) is the partial derivative of \(f\) with respect to \(x\). \(\alpha\) is known as the learning rate, which controls the step size gradient descent takes each iteration, typically chosen to be a small value, e.g. \(\alpha = 0.01.\) Values of \(\alpha\) that are too large cause learning to be suboptimal (by failing to converge), while values of \(\alpha\) that are too small make learning slow (by taking too long to converge).
The weight delta \(\Delta \vec{w} = \vec{w_{i+1}} - \vec{w_{i}}\) and bias delta \(\Delta b = b_{i+1} - b_i\) are calculated using the delta rule. The delta rule is a special case of backpropagation for single-layer perceptrons, and is used to calculate the updates (or deltas) of the perceptron parameters. The delta rule can be derived by consistent application of the chain rule and power rule for calculating the partial derivatives \(\frac{\partial E(X)}{\partial \vec{w_i}}\) and \(\frac{\partial E(X)}{\partial b_i}.\) For a perceptron with a mean squared error function and activation function \(g\), the delta rules for the weight vector \(\vec{w}\) and bias \(b\) are
\[\Delta \vec{w} = \frac{1}{N} \sum_{i=1}^N \alpha (y_i - o_i) g'(h_i) \vec{x_i}\\\\ \Delta b = \frac{1}{N} \sum_{i=1}^N \alpha (y_i - o_i) g'(h_i),\]
where \(o_i = g(\vec{w} \cdot \vec{x_i} + b)\) and \(h_i = \vec{w} \cdot \vec{x_i} + b\). Note that the presence of \(\vec{x_i}\) on the right side of the delta rule for \(\vec{w}\) implies that the weight vector's update delta is also a vector, which is expected.
Training the Perceptron
Thus, given a set of \(N\) input-output pairs \(X = \left\{\big(\vec{x_1}, y_1\big), \ldots, \big(\vec{x_N}, y_N\big)\right\},\) learning consists of iteratively updating the values of \(\vec{w}\) and \(b\) according to the delta rules. This consists of two distinct computational phases:
1. Calculate the forward values. That is, for \(X = \left\{\big(\vec{x_1}, y_1\big), \ldots, \big(\vec{x_N}, y_N\big)\right\},\) calculate \(h_i\) and \(o_i\) for all \(\vec{x_i}\).
2. Calculate the backward values. Using the partial derivatives of the error function, update the weight vector and bias according to gradient descent. Specifically, use the delta rules and the values calculated in the forward phase to calculate the deltas for each.
The backward phase is so named because in multi-layer perceptrons there is no simple delta rule, so calculation of the partial derivatives proceeds backwards from the error between the target output and actual output \(y_i - o_i\) (this is where backpropagation gets its name). In a single-layer perceptron, there is no backward flow of information (there is only one "layer" of parameters), but the naming convention applies all the same.
Once the backward values are computed, they may be used to update the values of the weight vector \(\vec{w}\) and bias \(b\). The process repeats until the error function \(E(X)\) converges. Once the error function has converged, the weight vector \(\vec{w}\) and bias \(b\) can be fixed, and the forward phase used to calculate predicted values \(o\) of the true output \(y\) for any input \(x\). If the perceptron has learned the underlying function mapping inputs to outputs \(\big(\)i.e. not just remembered every pair of \((\vec{x_i}, y_i)\big),\) it will even predict the correct values for input-output pairs it was not trained on, known as generalization. Ultimately, generalization is the primary goal of supervised learning, since it is desirable and a practical necessity to learn an unknown function based on a small sample of the set of all possible input-output pairs.
Limitations
It was mentioned earlier that single-layer perceptrons are linear classifiers. That is, they can only learn linearly separable patterns. Linearly separable patterns are datasets or functions that can be separated by a linear boundary (a line or hyperplane). Marvin Minsky and Seymour Papert showed in their seminal 1969 book Perceptrons that it was impossible for a perceptron to learn even simple non-linearly separable functions such as the XOR function. The XOR, or "exclusive or", function is a simple function on two binary inputs and is often found in bit twiddling hacks. A plot of and truth table for XOR is below.
 XOR function, with white dots and black dots representing outputs of \(0\) and \(1\), respectively
XOR function, with white dots and black dots representing outputs of \(0\) and \(1\), respectively
| \(X_1\) | \(X_2\) | \(XOR\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Notice that, for the plot of the XOR function, it is impossible to find a linear boundary that separates the black and white inputs from one another. This is because XOR is not a linearly separable function, and by extension, perceptrons cannot learn the XOR function. Similar analogs exist in higher dimensions, i.e. more than two inputs.
Many other (indeed, most other) functions are not linearly separable, so what is needed is an extension to the perceptron. The obvious extension is to add more layers of units so that there are nonlinear computations in between the input and output. For a long time, it was assumed by many in the field that adding more layers of units would fail to solve the linear separability problem (even though Minsky and Papert knew that such an extension could learn the XOR function), so research in the field of artificial neural networks stagnated for a good decade. Indeed, this assumption turned out to be very wrong, as multi-layer perceptrons, covered in the next section, can learn practically any function of interest.
Multi-layer Perceptron
The mulit-layer perceptron (MLP) is an artificial neural network composed of many perceptrons. Unlike single-layer perceptrons, MLPs are capable of learning to compute non-linearly separable functions. Because they can learn nonlinear functions, they are one of the primary machine learning techniques for both regression and classification in supervised learning.
Layers
MLPs are usually organized into something called layers. As discussed in the sections on neural networks as graphs and neural networks as layers, the generalized artificial neural network consists of an input layer, some number (possibly zero) of hidden layers, and an output layer. In the case of a single-layer perceptron, there are no hidden layers, so the total number of layers is two. MLPs, on the other hand, have at least one hidden layer, each composed of multiple perceptrons. An example of a feedforward neural network with two hidden layers is below.
 A four-layer feedforward neural network
A four-layer feedforward neural network
It was mentioned in the introduction that feedforward neural networks have the property that information (i.e. computation) flows forward through the network, i.e. there are no loops in the computation graph (it is a directed acyclic graph, or DAG). Another way of saying this is that the layers are connected in such a way that no layer's output depends on itself. In the above figure, this is clear since each layer (other than the input layer) is only connected to the layer directly to its left. Feedforward neural networks, by having DAGs for their computation graphs, have a greatly simplified learning algorithm compared to recurrent neural networks, which have cycles in their dependency graphs.
Generally speaking, if one is given a graph representing a feedforward network, it can always be grouped into layers such that each layer depends only on layers to its left. This can be done by performing a topological sort on the nodes and grouping nodes with the same depth into the same layer, where layer \(l_i\) consists of all nodes in the graph with depth \(i\) in the topological sort. Then, arranging layers \(l_0, \dots, l_k\) from left to right, each layer's nodes will only depend on nodes from layers to its left.
Formal Definition
The following defines a prototypical \(m\)-layer \((\)meaning \(m-2\) hidden layers\()\) MLP that computes a one-dimensional output \(o\) on an \(n\)-dimensional input \(\vec{x} = \{x_1, \dots, x_n\}\).
Assume that
- The output perceptron has an activation function \(g_o\) and hidden layer perceptrons have activation functions \(g\).
- Every perceptron in layer \(l_i\) is connected to every perceptron in layer \(l_{i-1};\) layers are "fully connected." Thus, every perceptron depends on the outputs of all the perceptrons in the previous layer (this is without loss of generality since the weight connecting two perceptrons can still be zero, which is the same as no connection being present).
- There are no connections between perceptrons in the same layer.
 A fully connected MLP on three inputs with two hidden layers, each with four perceptrons
A fully connected MLP on three inputs with two hidden layers, each with four perceptrons
and use the following denotation:
\(w_{ij}^k:\) weight for perceptron \(j\) in layer \(l_k\) for incoming node \(i\) \((\)a perceptron if \(k \ge 1)\) in layer \(l_{k - 1}\)
\(b_i^k:\) bias for perceptron \(i\) in layer \(l_k\)
\(h_i^k:\) product sum plus bias for perceptron \(i\) in layer \(l_k\)
\(o_i^k:\) output for node \(i\) in layer \(l_k\)
\(r_k:\) number of nodes in layer \(l_k\)
\( \)
\(\vec{w_i^k}:\) weight vector for perceptron \(i\) in layer \(l_k\), i.e. \(\vec{w}_i^k = \big\{w_{1i}^k, \ldots, w_{r_ki}^k\big\}\)
\(\vec{o^k}:\) output vector for layer \(l_k\), i.e. \(\vec{o^k} = \big\{o_1^k, \ldots, o_{r_k}^k\big\}\)
Then, computation of the MLP's output \(o\) proceeds according to the following steps:
Initialize the input layer \(l_0\)
Set the values of the outputs \(o_i^0\) for nodes in the input layer \(l_0\) to their associated inputs in the vector \(\vec{x} = \{x_1, \dots, x_n\}\), i.e. \(o_i^0 = x_i\).Calculate the product sums and outputs of each hidden layer in order from \(l_1\) to \(l_{m-1}\)
For \(k\) from \(1\) to \(m-1,\)
a. compute \(h_i^k = \vec{w_i^k} \cdot \vec{o^{k-1}} + b_i^k = b_i^k + \sum_{j = 1}^{r_{k-1}} w_{ji}^k o_j^{k-1}\) for \(i = 1, \ldots, r_k;\)
b. compute \(o_i^k = g\big(h_i^k\big)\) for \(i = 1, \ldots, r_k.\)Compute the output \(y\) for output layer \(l_m\)
a. Compute \(h_1^m = \vec{w_1^m} \cdot \vec{o^{m-1}} + b_1^m = b_1^m + \sum_{j = 1}^{r_{m-1}} w_{j1}^k o_j^{k-1}.\)
b. Compute \(o = o_1^m = g_o(h_1^m).\)
Training MLPs
Like the single-layer-perceptron, given a set of \(N\) input-output pairs \(X = \left\{\big(\vec{x_1}, y_1\big), \ldots, \big(\vec{x_N}, y_N\big)\right\},\) learning consists of iteratively updating the values of \(\vec{w_i^k}\) and \(b_i^k\) in order to minimize the mean squared error (MSE)
\[E(X) = \frac{1}{2N} \sum_{i=1}^N \left(o_i - y_i\right)^2,\]
where \(o_i\) denotes the output \(o\) (the result of step 3 in the computation above) of the MLP on input \(\vec{x_i}\). Analogous to the single-layer perceptron, minimizing \(E(X)\) with respect to all \(w_{ij}^k\) and \(b_i^k\) will yield a good classification boundary. Using gradient descent to adjust the parameters \(w_{ij}^k\) and \(b_i^k\) with a learning rate of \(\alpha\) yields the following delta equations for each iteration:
\[\Delta w_{ij}^k = - \alpha \frac{\partial E(X)}{\partial w_{ij}^k}\\\\ \Delta b_i^k = - \alpha \frac{\partial E(X)}{\partial b_i^k}.\]
The expansion of the right-hand side of the delta rules can be found using backpropagation, so called because the gradient information flows backwards through the network (i.e. in the direction opposite the output computation flow). This gradient flow originates in the final layer \(l_m\), proportional to the difference between the target output \(y\) and actual output \(o\).
Thus, one iteration of training for MLPs consists of two distinct computational phases:
Here is a tutorial helps you to understand how Python implements feed forward neural networks using Numpy.
- Calculate the forward values. That is, for \(X = \left\{\big(\vec{x_1}, y_1\big), \ldots, \big(\vec{x_N}, y_N\big)\right\},\) calculate all \(h_i^k\) and \(o_i^k\) for all \(\vec{x_i}\).
- Calculate the backward values. Using the partial derivatives of the error function, update the weights \(w_{ij}^k\) and biases \(b_i^k\) according to gradient descent. Specifically, use backpropagation and the values calculated in the forward phase to calculate the deltas for each.