Hungarian Maximum Matching Algorithm

The Hungarian matching algorithm, also called the Kuhn-Munkres algorithm, is a $O\big(|V|^3\big)$ algorithm that can be used to find maximum-weight matchings in bipartite graphs, which is sometimes called the assignment problem. A bipartite graph can easily be represented by an adjacency matrix, where the weights of edges are the entries. Thinking about the graph in terms of an adjacency matrix is useful for the Hungarian algorithm.

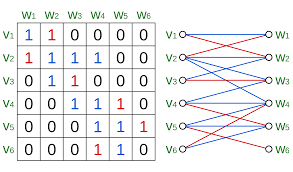A matching corresponds to a choice of 1s in the adjacency matrix, with at most one 1 in each row and in each column.

The Hungarian algorithm solves the following problem:

In a complete bipartite graph $G$, find the maximum-weight matching. (Recall that a maximum-weight matching is also a perfect matching.)

This can also be adapted to find the minimum-weight matching.

Say you are having a party and you want a musician to perform, a chef to prepare food, and a cleaning service to help clean up after the party. There are three companies that provide each of these three services, but one company can only provide one service at a time (i.e. Company B cannot provide both the cleaners and the chef). You are deciding which company you should purchase each service from in order to minimize the cost of the party. You realize that is an example of the assignment problem, and set out to make a graph out of the following information:

$\quad$ Company$\quad$	$\quad$ Cost for Musician$\quad$	$\quad$ Cost for Chef$\quad$	$\quad$ Cost for Cleaners$\quad$
$\quad$ Company A$\quad$	$\quad$ $108$\quad$	$\quad$ $125$\quad$	$\quad$ $150$\quad$
$\quad$ Company B$\quad$	$\quad$ $150$\quad$	$\quad$ $135$\quad$	$\quad$ $175$\quad$
$\quad$ Company C$\quad$	$\quad$ $122$\quad$	$\quad$ $148$\quad$	$\quad$ $250$\quad$

Can you model this table as a graph? What are the nodes? What are the edges?

Show Answer

The nodes are the companies and the services. The edges are weighted by the price.

What are some ways to solve the problem above? Since the table above can be thought of as a $3 \times 3$ matrix, one could certainly solve this problem using brute force, checking every combination and seeing what yields the lowest price. However, there are $n!$ combinations to check, and for large $n$, this method becomes very inefficient very quickly.

With the cost matrix from the example above in mind, the Hungarian algorithm operates on this key idea: if a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an optimal assignment for the original cost matrix.

The Hungarian Method ^[1]

1. Subtract the smallest entry in each row from all the other entries in the row. This will make the smallest entry in the row now equal to 0.

2. Subtract the smallest entry in each column from all the other entries in the column. This will make the smallest entry in the column now equal to 0.

3. Draw lines through the row and columns that have the 0 entries such that the fewest lines possible are drawn.

4. If there are $n$ lines drawn, an optimal assignment of zeros is possible and the algorithm is finished. If the number of lines is less than $n$, then the optimal number of zeroes is not yet reached. Go to the next step.

5. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3.

Solve for the optimal solution for the example in the introduction using the Hungarian algorithm described above.

---

Here is the initial adjacency matrix:

Subtract the smallest value in each row from the other values in the row:

Now, subtract the smallest value in each column from all other values in the column:

Draw lines through the row and columns that have the 0 entries such that the fewest possible lines are drawn:

There are 2 lines drawn, and 2 is less than 3, so there is not yet the optimal number of zeroes.

Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3.

2 is the smallest entry.

First, subtract from the uncovered rows:

Now add to the covered columns:

Now go back to step 3, drawing lines through the rows and columns that have 0 entries:

There are 3 lines (which is $n$), so we are done. The assignment will be where the 0's are in the matrix such that only one 0 per row and column is part of the assignment.

Replace the original values:

The Hungarian algorithm tells us that it is cheapest to go with the musician from company C, the chef from company B, and the cleaners from company A.

We can verify this by brute force.

• 108 + 135 + 250 = 493
• 108 + 148 + 175 = 431
• 150 + 125 + 250 = 525
• 150 + 148 + 150 = 448
• 122 + 125 + 175 = 422
• 122 + 135 + 150 = 407.

We can see that 407 is the lowest price and matches the assignment the Hungarian algorithm determined. $_\square$

The Hungarian algorithm can also be executed by manipulating the weights of the bipartite graph in order to find a stable, maximum (or minimum) weight matching. This can be done by finding a feasible labeling of a graph that is perfectly matched, where a perfect matching is denoted as every vertex having exactly one edge of the matching.

How do we know that this creates a maximum-weight matching?

A feasible labeling on a perfect match returns a maximum-weighted matching.

Suppose each edge $e$ in the graph $G$ connects two vertices, and every vertex $v$ is covered exactly once. With this, we have the following inequality: $$w(M’) = \sum_{e\ \epsilon\ E} w(e) \leq \sum_{e\ \epsilon\ E } \big(l(e_x) + l(e_y)\big) = \sum_{v\ \epsilon\ V} l(v),$$ where $M’$ is any perfect matching in $G$ created by a random assignment of vertices, and $l(x)$ is a numeric label to node $x$.

This means that $\sum_{v\ \epsilon\ V}\ l(v)$ is an upper bound on the cost of any perfect matching.

Now let $M$ be a perfect match in $G$, then $$w(M) = \sum_{e\ \epsilon\ E} w(e) = \sum_{v\ \epsilon\ V}\ l(v).$$

So $w(M’) \leq w(M)$ and $M$ is optimal. $_\square$

Start the algorithm by assigning any weight to each individual node in order to form a feasible labeling of the graph $G$. This labeling will be improved upon by finding augmenting paths for the assignment until the optimal one is found.

A feasible labeling is a labeling such that

$l(x) + l(y) \geq w(x,y)\ \forall x \in X, y \in Y$, where $X$ is the set of nodes on one side of the bipartite graph, $Y$ is the other set of nodes, $l(x)$ is the label of $x$, etc., and $w(x,y)$ is the weight of the edge between $x$ and $y$.

A simple feasible labeling is just to label a node with the number of the largest weight from an edge going into the node. This is certain to be a feasible labeling because if $A$ is a node connected to $B$, the label of $A$ plus the label of $B$ is greater than or equal to the weight $w(x,y)$ for all $y$ and $x$.

A feasible labeling of nodes, where labels are in red ^[2].

Imagine there are four soccer players and each can play a few positions in the field. The team manager has quantified their skill level playing each position to make assignments easier.

How can players be assigned to positions in order to maximize the amount of skill points they provide?

The algorithm starts by labeling all nodes on one side of the graph with the maximum weight. This can be done by finding the maximum-weighted edge and labeling the adjacent node with it. Additionally, match the graph with those edges. If a node has two maximum edges, don’t connect them.

Although Eva is the best suited to play defense, she can't play defense and mid at the same time!

If the matching is perfect, the algorithm is done as there is a perfect matching of maximum weights. Otherwise, there will be two nodes that are not connected to any other node, like Tom and Defense. If this is the case, begin iterating.

Improve the labeling by finding the non-zero label vertex without a match, and try to find the best assignment for it. Formally, the Hungarian matching algorithm can be executed as defined below:

The Hungarian Algorithm for Graphs ^[3]

Given: the labeling $l$, an equality graph $G_l = (V, E_l)$, an initial matching $M$ in $G_l$, and an unmatched vertex $u \in V$ and $u \notin M$

Augmenting the matching

1. A path is augmenting for $M$ in $G_l$ if it alternates between edges in the matching and edges not in the matching, and the first and last vertices are free vertices, or unmatched, in $M$. We will keep track of a candidate augmenting path starting at the vertex $u$.

2. If the algorithm finds an unmatched vertex $v$, add on to the existing augmenting path $p$ by adding the $u$ to $v$ segment.

3. Flip the matching by replacing the edges in $M$ with the edges in the augmenting path that are not in $M$ $($in other words, the edges in $E_l - M).$

Improving the labeling

1. $S \subseteq X$ and $T \subseteq Y,$ where $S$ and $T$ represent the candidate augmenting alternating path between the matching and the edges not in the matching.

2. Let $N_l(S)$ be the neighbors to each node that is in $S$ along edges in $E_l$ such that $N_l(S) = \{v|\forall u \in S: (u,v) \in E_l\}$.

3. If $N_l(S) = T$, then we cannot increase the size of the alternating path (and therefore can't further augment), so we need to improve the labeling.

4. Let $\delta_l$ be the minimum of $l(u) + l(v) - w(u,v)$ over all of the $u \in S$ and $v \notin T$.

5. Improve the labeling $l$ to $l'$:

   • If $r \in S,$ then $l'(r) = l(r) - \delta_l,$
   • If $r \in T,$ then $l'(r) = l(r) + \delta_l.$
   • If $r \notin S$ and $r \notin T,$ then $l'(r) = l(r).$

$l'$ is a valid labeling and $E_l \subset E_{l'}.$

Putting it all together: The Hungarian Algorithm

1. Start with some matching $M$, a valid labeling $l$, where $l$ is defined as the labelling $\forall x \in X, y \in Y| l(y) = 0, l(x) = \text{ max}_{y \in Y}(w\big(x, y)\big)$.

2. Do these steps until a perfect matching is found $($when $M$ is perfect$):$

   • (a) Look for an augmenting path in $M.$
   • (b) If an augmenting path does not exist, improve the labeling and then go back to step (a).

Each step will increase the size of the matching $M$ or it will increase the size of the set of labeled edges, $E_l$. This means that the process will eventually terminate since there are only so many edges in the graph $G$.^[4]

When the process terminates, $M$ will be a perfect matching. By the Kuhn-Munkres theorem, this means that the matching is a maximum-weight matching.

The algorithm defined above can be implemented in the soccer scenario. First, the conflicting node is identified, implying that there is an alternating tree that must be reconfigured.

There is an alternating path between defense, Eva, mid, and Tom.

To find the best appropriate node, find the minimum $\delta_l$, as defined in step 4 above, where $l_u$ is the label for player $u,$ $l_v$ is the label for position $v,$ and $w_{u, v}$ is the weight on that edge.

The $\delta_l$ of each unmatched node is computed, where the minimum is found to be a value of 2, between Tom playing mid $(8 + 0 - 6 = 2).$

The labels are then augmented and the new edges are graphed in the example. Notice that defense and mid went down by 2 points, whereas Eva’s skillset got back two points. However, this is expected as Eva can't play in both positions at once.

Augmenting path leads to relabeling of nodes, which gives rise to the maximum-weighted path.

These new edges complete the perfect matching of the graph, which implies that a maximum-weighted graph has been found and the algorithm can terminate.

The complexity of the algorithm will be analyzed using the graph-based technique as a reference, yet the result is the same as for the matrix-based one.

Algorithm analysis^[3]

• At each $a$ or $b$ step, the algorithm adds one edge to the matching and this happens $O\big(|V|\big)$ times.

• It takes $O\big(|V|\big)$ time to find the right vertex for the augmenting (if there is one at all), and it is $O\big(|V|\big)$ time to flip the matching.

• Improving the labeling takes $O\big(|V|\big)$ time to find $\delta_l$ and to update the labelling accordingly. We might have to improve the labeling up to $O\big(|V|\big)$ times if there is no augmenting path. This makes for a total of $O\big(|V|^2\big)$ time.

• In all, there are $O\big(|V|\big)$ iterations each taking $O\big(|V|\big)$ work, leading to a total running time of $O\big(|V|^3\big)$.

• Matching Algorithms

1. Bruff, D. The Assignment Problem and the Hungarian Method. Retrieved June 26, 2016, from http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf
2. Golin, M. Bipartite Matching & the Hungarian Method. Retrieved Retrieved June 26th, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
3. Grinman, A. The Hungarian Algorithm for Weighted Bipartite Graphs. Retrieved June 26, 2016, from http://math.mit.edu/~rpeng/18434/hungarianAlgorithm.pdf
4. Golin, M. Bipartite Matching & the Hungarian Method. Retrieved June 26, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf