Matching Algorithms (Graph Theory)

Matching algorithms are algorithms used to solve graph matching problems in graph theory. A matching problem arises when a set of edges must be drawn that do not share any vertices.

Graph matching problems are very common in daily activities. From online matchmaking and dating sites, to medical residency placement programs, matching algorithms are used in areas spanning scheduling, planning, pairing of vertices, and network flows. More specifically, matching strategies are very useful in flow network algorithms such as the Ford-Fulkerson algorithm and the Edmonds-Karp algorithm.

Graph matching problems generally consist of making connections within graphs using edges that do not share common vertices, such as pairing students in a class according to their respective qualifications; or it may consist of creating a bipartite matching, where two subsets of vertices are distinguished and each vertex in one subgroup must be matched to a vertex in another subgroup. Bipartite matching is used, for example, to match men and women on a dating site.

Alternating and Augmenting Paths

Graph matching algorithms often use specific properties in order to identify sub-optimal areas in a matching, where improvements can be made to reach a desired goal. Two famous properties are called augmenting paths and alternating paths, which are used to quickly determine whether a graph contains a maximum, or minimum, matching, or the matching can be further improved.

$Graph\ 1$ shows all the edges, in blue, that connect the bipartite graph. The goal of a matching algorithm, in this and all bipartite graph cases, is to maximize the number of connections between vertices in subset $A$, above, to the vertices in subset $B$, below.

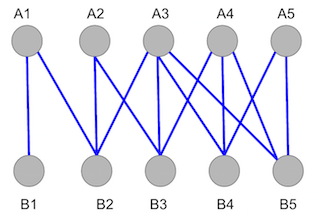$$Graph\ 1$. Unmatched bipartite graph$ $Graph\ 1$. Unmatched bipartite graph

Most algorithms begin by randomly creating a matching within a graph, and further refining the matching in order to attain the desired objective.

$Random initial matching , $M$, of Graph 1 represented by the red edges$ Random initial matching , $M$, of Graph 1 represented by the red edges

$Graph\ 1$, with the matching, $M$, is said to have an alternating path if there is a path whose edges are in the matching, $M$, and not in the matching, in an alternating fashion. An alternating path usually starts with an unmatched vertex and terminates once it cannot append another edge to the tail of the path while maintaining the alternating sequence.

$An alternating path in Graph 1 is represented by red edges, in $M$, joined with green edges, not in $M$.$ An alternating path in Graph 1 is represented by red edges, in $M$, joined with green edges, not in $M$.

An augmenting path, then, builds up on the definition of an alternating path to describe a path whose endpoints, the vertices at the start and the end of the path, are free, or unmatched, vertices; vertices not included in the matching. Finding augmenting paths in a graph signals the lack of a maximum matching.

The matching, $M$, for $Graph\ 1$, does not start and end on free vertices, so it does not have an augmenting path. This implies that the matching $M$ is a maximum matching.

If there exists an augmenting path, $p$, in a matching, $M$, then $M$ is not a maximum matching. Alternatively, if $M$ is a maximum matching, then it has no augmenting path.

Does the matching in this graph have an augmenting path, or is it a maximum matching?

Try to draw out the alternating path and see what vertices the path starts and ends at.

The graph does contain an alternating path, represented by the alternating colors below.

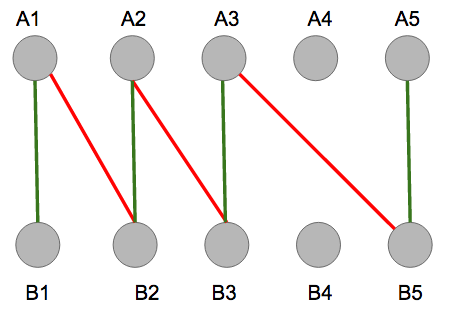
Once the path is built from $B1$ to node $A5$, no more red edges, edges in $M$, can be added to the alternating path, implying termination. Notice that the end points are both free vertices, so the path is alternating and this matching is not a maximum matching.

Augmenting paths in matching problems are closely related to augmenting paths in maximum flow problems, such as the max-flow min-cut algorithm, as both signal sub-optimality and space for further refinement. In max-flow problems, like in matching problems, augmenting paths are paths where the amount of flow between the source and sink can be increased. ^[1]

Graph Labeling

The majority of realistic matching problems are much more complex than those presented above. This added complexity often stems from graph labeling, where edges or vertices labeled with quantitative attributes, such as weights, costs, preferences or any other specifications, which adds constraints to potential matches.

A common characteristic investigated within a labeled graph is a known as feasible labeling, where the label, or weight assigned to an edge, never surpasses in value to the addition of respective vertices’ weights. This property can be thought of as the triangle inequality.

Feasible Labeling

$l(x) + l(y) \geq w(x,y), \forall x \in X,\ \forall y \in Y$

Where $l(x)$ is the label of $x$, $w(x,y)$ is the weight of the edge between $x$ and $y$, $X$ is the set of nodes on one side of the bipartite graph, and $Y$ is the set of nodes on the other side of the graph.

A feasible labeling acts opposite an augmenting path; namely, the presence of a feasible labeling implies a maximum-weighted matching, according to the Kuhn-Munkres Theorem.

The Kuhn-Munkres Theorem

If there is a feasible labeling within items in $M$, and $M$ is a perfect matching, then $M$ is a maximum-weight matching.

Conversely, if the labeling within $M$ is feasible and $M$ is a maximum-weight matching, then $M$ is a perfect matching.

When a graph labeling is feasible, yet vertices’ labels are exactly equal to the weight of the edges connecting them, the graph is said to be an equality graph.

Equality Graph

An equality graph for a graph $G = (V, E_t)$ contains the following constraint for all edges in a matching:

$E_l = \{(x,y)\} : l(x) + l(y) = w(x,y)\}$

Equality graphs are helpful in order to solve problems by parts, as these can be found in subgraphs of the graph $G$, and lead one to the total maximum-weight matching within a graph.

If an equality subgraph, $G_l$, has a perfect matching, $M'$, then $M'$ is a maximum-weight matching in $G$.

A variety of other graph labeling problems, and respective solutions, exist for specific configurations of graphs and labels; problems such as graceful labeling, harmonious labeling, lucky-labeling, or even the famous graph coloring problem.

Hungarian Maximum Matching Algorithm

A common bipartite graph matching algorithm is the Hungarian maximum matching algorithm, which finds a maximum matching by finding augmenting paths. More formally, the algorithm works by attempting to build off of the current matching, $M$, aiming to find a larger matching via augmenting paths. Each time an augmenting path is found, the number of matches, or total weight, increases by 1. The main idea is to augment $M$ by the shortest augmenting path making sure that no constraints are violated.

The algorithm starts with any random matching, including an empty matching. It then constructs a tree using a breadth-first search in order to find an augmenting path. If the search finds an augmenting path, the matching gains one more edge. Once the matching is updated, the algorithm continues and searches again for a new augmenting path. If the search is unsuccessful, the algorithm terminates as the current matching must be the largest-size matching possible.^[2]

The time complexity of the original algorithm is $O(|V|^4)$, where $|V|$ is the total number of vertices in the graph. The algorithm was later improved to $O(|V|^3)$ time using better performing data structures.

Blossom Algorithm

Unfortunately, not all graphs are solvable by the Hungarian Matching algorithm as a graph may contain cycles that create infinite alternating paths. In this specific scenario, the blossom algorithm can be utilized to find a maximum matching. Also known as the Edmonds’ matching algorithm, the blossom algorithm improves upon the Hungarian algorithm by shrinking odd-length cycles in the graph down to a single vertex in order to reveal augmenting paths and then use the Hungarian Matching algorithm.

A blossom is a cycle in $G$ consisting of $2k + 1$ edges of which exactly $k$ belong to $M$, and where one of the vertices, $v$, the base, in the cycle is at the head of an alternating path of even length, the path being named stem, to an exposed vertex, $w$^[3].

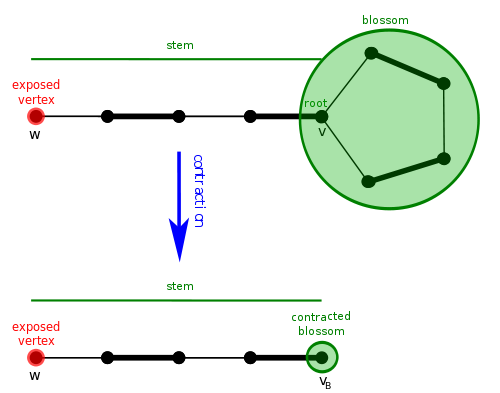Shrinking of a cycle using the blossom algorithm.^[4]

The blossom algorithm works by running the Hungarian algorithm until it runs into a blossom, which it then shrinks down into a single vertex. Then, it begins the Hungarian algorithm again. If another blossom is found, it shrinks the blossom and starts the Hungarian algorithm yet again, and so on until no more augmenting paths or cycles are found. ^[5]

The total runtime of the blossom algorithm is $O(|E||V|^2)$, for $|E|$ total edges and $|V|$ total vertices in the graph. ^[6]

Hopcroft–Karp Algorithm

The poor performance of the Hungarian Matching Algorithm sometimes deems it unuseful in dense graphs, such as a social network. Improving upon the Hungarian Matching algorithm is the Hopcroft–Karp algorithm, which takes a bipartite graph, $G(E,V)$, and outputs a maximum matching. The time complexity of this algorithm is $O(|E| \sqrt{|V|})$ in the worst case scenario, for $|E|$ total edges and $|V|$ total vertices found in the graph.

The Hopcroft-Karp algorithm uses techniques similar to those used in the Hungarian algorithm and the Edmonds’ blossom algorithm. Hopcroft-Karp works by repeatedly increasing the size of a partial matching via augmenting paths. Unlike the Hungarian Matching Algorithm, which finds one augmenting path and increases the maximum weight by of the matching by $1$ on each iteration, the Hopcroft-Karp algorithm finds a maximal set of shortest augmenting paths during each iteration, allowing it to increase the maximum weight of the matching with increments larger than $1$.

In practice, researchers have found that Hopcroft-Karp is not as good as the theory suggests — it is often outperformed by breadth-first and depth-first approaches to finding augmenting paths.^[1]

References

, . Hopcroft–Karp algorithm. Retrieved June 19, 2016, from https://en.wikipedia.org/wiki/Hopcroft%E2%80%93Karp_algorithm
, . The Hungarian Maximum Matching Algorithm. Retrieved June 19, 2016, from http://demonstrations.wolfram.com/TheHungarianMaximumMatchingAlgorithm/
, . Blossom Algorithm. Retrieved June 19, 2016, from https://en.wikipedia.org/wiki/Blossom_algorithm
, A. Edmonds blossom.svg. Retrieved June 19, 2016, from https://en.wikipedia.org/wiki/File:Edmonds_blossom.svg
Kusner, M. Edmonds’ Blossom Algorithm. Retrieved June 19, 2016, from http://matthewkusner.com/MatthewKusner_BlossomAlgorithmReport.pdf
Shoemaker, A., & Vare, S. Edmonds’ Blossom Algorithm. Retrieved June 19, 2016, from http://stanford.edu/~rezab/dao/projects_reports/shoemaker_vare.pdf

Computer Science Fundamentals

Contents