Matching (Graph Theory)

In graph theory, a matching in a graph is a set of edges that do not have a set of common vertices. In other words, a matching is a graph where each node has either zero or one edge incident to it.

Graph matching is not to be confused with graph isomorphism. Graph isomorphism checks if two graphs are the same whereas a matching is a particular subgraph of a graph.

The subset of edges colored red represent a matching in both graphs. ^{[1] [2]}

Graph matching has applications in flow networks, scheduling and planning, modeling bonds in chemistry, graph coloring, the stable marriage problem, neural networks in artificial intelligence and more.

Many graph matching algorithms exist in order to optimize for the parameters necessary dictated by the problem at hand.

Say there is a group of candidates and a set of jobs, and each candidate is qualified for at least one of the jobs. We can use graph matching to see if there is a way we can give each candidate a job they are qualified for. The graph below shows all of the candidates and jobs and there is an edge between a candidate and each job they are qualified for.

Is there a way to assign each person to a single job they are qualified such that every job has only one person assigned to it?

Show Answer

Yes, there is a way to assign each person to a single job by matching each worker with a designated job. Although the solution to this problem can be solved quickly without any efficient algorithms, problems of this type can get rather complicated as the number of nodes increases, such as in a social network.

Matching

Given a graph $G = (V, E)$, a matching is a subgraph of $G$, $P$, where every node has a degree of at most 1. The matching consists of edges that do not share nodes.

Maximal matching

A matching, $P$, of graph, $G$, is said to be maximal if no other edges of $G$ can be added to $P$ because every node is matched to another node. In other words, if an edge that is in $G$ and is not in $P$ is added to $P$, it would cause $P$ to no longer be a matching graph, as a node will have more than one edge incident to it. $P$ is also a maximal matching if it is not a proper subset of any other matching in $G$; if every edge in $G$ has a non-empty intersection with at least one edge in $P$ ^[3]. Note that a maximal matching is not necessarily the subgraph that provides the maximum number of matches possible within a graph.

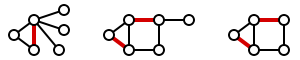Maximal matchings shown by the subgraph of red edges. ^[4]

Maximum matching

A matching is a maximum matching if it is a matching that contains the largest possible number of edges matching as many nodes as possible. Simply stated, a maximum matching is the maximal matching with the maximum number of edges. Every maximum matching is maximal, but not every maximal matching is a maximum matching.

In weighted graphs, sometimes it is useful to find a matching that maximizes the weight.

A group of students are being paired up as partners for a science project. Each student has determined his or her preference list for partners, ranking each classmate with a number indicating preference, where 20 is the highest ranking one can give a best friend, and rankings cannot be repeated as there are 21 students total. The teacher decides to model this problem as a graph by making an edge between each student, assigning a weight to each edge equal to the average of each student’s ranking of each other. The teacher realizes that in order to maximize the class’ overall happiness, she must find the maximum matching for the entire class.

Minimum weight matchings can also be performed if the purpose of a maximal matching is to minimize the overall weight of the graph; if the teacher in the example above asked students to rank their best friends in ascending order.

A graph may contain more than one maximum matching if the same maximum weight is achieved with a different subset of edges. The size, or total weight, of the maximum matching in a graph is called the matching number.

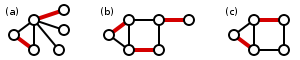Maximum matchings shown by the subgraph of red edges.^[5]

Perfect matching

A perfect matching is a matching where every vertex is connected to exactly one edge; where the matching matches all vertices in the graph. In an unweighted graph, every perfect matching is a maximum matching and is, therefore, a maximal matching as well. If the graph is weighted, there can be many perfect matchings of different matching numbers. Formally speaking, a matching of a graph $G = (V, E)$ is perfect if it has $\frac{|V |} {2}$ edges.

A near-perfect matching, on the other hand, can occur in a graph that has an odd number of vertices. In this case, it is clear that a perfect matching as described above is impossible as one node will be left unmatched. This scenario also results in a maximum matching for a graph with an odd number of nodes.

In order to model matching problems more clearly, graphs are usually transformed into bipartite graph, where its vertex set is divided into two disjoint sets, $V_1$ and $V_2$, where $V = V_1 \cup V_2$ and all edges connect vertices between $V_1$ and $V_2$.

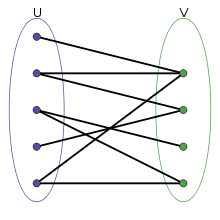A bipartite graph is represented by grouping vertices into two disjoint sets, $U$, and $V$.^[6]

Find a matching graph within the bipartite graph above.

Show Answer

Here’s one possible matching in the graph. Another matching may be present — remember it is any subgraph where each of the vertices in the subgraph has only one edge coming out of it. This is a near-perfect matching since only one vertex is not included in the matching, but remember a matching is any subgraph of a graph where any node in the subgraph has one edge coming out of it.

The matching process is generally used to answer questions related to graphs, such as the vertex cover, or network, such as flow or social networks; the most famous problem of this kind being the stable marriage problem.

The Stable Marriage Problem

The purpose of the stable marriage problem is to facilitate matchmaking between two sets of people. Given a list of potential matches among an equal number of brides and grooms, the stable marriage problem gives a necessary and sufficient condition on the list for everyone to be married to an agreeable match. This theorem can be applied to any situation where two vertices must be matched together so as to maximize utility, or overall happiness.

There are $6$ gifts labeled $1,2,3,4,5,6$) under the Christmas tree, and $5$ children receiving them: Alice, Bob, Charles, Danielle, and Edward. Can the gifts be distributed to each person so that each one of them gets a gift they’ll like?

If none of them like any of the gifts, then the solution may be impossible and nobody will enjoy their presents. Even if slight preferences exist, distribution can be quite difficult if, say, none of them like gifts $5$ or $6$, then only $4$ gifts will be have to be distributed amongst the $5$ children. On another scenario, suppose that

Alice wants gifts 1, 3.
Bob wants gifts 2, 4, 5, 6.
Charles wants gifts 2, 3.
Dot wants gifts 1, 2, 3.
Edward wants gifts 2.

How can each kid’s happiness be maximized given their respective gift preferences?

There is still no way to distribute the gifts to make everyone happy. In fact, notice that four of the children, Alice, Charles, Danielle, and Edward, only want one of the first three gifts, which makes it clear that the problem is impossible and one of them will be stuck with a gift they will not enjoy.

It turns out, however, that this is the only way for the problem to be impossible. As long as there isn't a subset of children that collectively like fewer gifts than there are children in the subset, there will always be a way to give everyone something they want. This is the crux of Hall's marriage theorem.

This is just a brief overview of the problem. For more on Hall’s Stable Marriage Theorem, refer to the Stable Marriage page and the applications of the Stable Marriage Theorem page.

Vertex Cover

Vertex cover, sometimes called node cover, is a famous optimization problem that uses matching. For a graph $G = (V,E)$, a vertex cover is a set of vertices $V' \in V$ such that every edge in the graph has at least one endpoint that is in $V'$. Below are two graphs and their vertex cover sets represented in red. Basically, a vertex cover "covers" all of the edges.

The vertex covers above do not contain the minimum number of vertices for a vertex cover^[7]

An art museum is filled with famous paintings so security must be airtight. It is of paramount importance to assure nobody can steal these expensive artworks, so the security personnel must install security cameras to closely monitor every painting. To determine where to place these cameras in the hallways so that all paintings are guarded, security can look at a map of the museum and model it as a graph where the hallways are the edges and the corners are the nodes. If there are five paintings lined up along a single wall in a hallway with no turns, a single camera at the beginning of the hall will guard all five paintings. This way, the security staff can determine the vertex cover set to find out where to place the cameras.

To further improve upon the placement of cameras, the security staff can minimize the number of cameras needed to protect the entire museum by implementing an algorithm called minimum vertex cover.

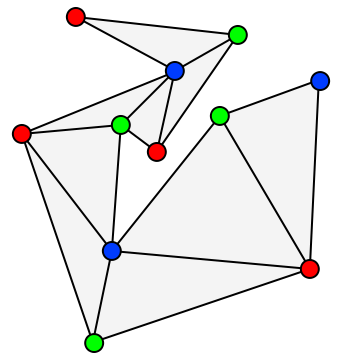The vertex cover is not unique. Each set vertices; blue, green, and red, form a vertex cover. ^[8]

A more theoretical concept relating to vertex cover is Konig's theorem that states that for any bipartite graph, the maximum size of a matching is equal to the minimum size of a vertex cover.

Transportation Theory

Matching algorithms also have tremendous application in resource allocation problems, also known as flow network problems. In mathematics and economics, the study of resource allocation and optimization in travel is called transportation theory. ^[9]

In a large city, $N$ factories make computers and $N$ stores sell computers. Each factory can ship its computers to only one store, and each store will receive a shipment from exactly one factory. If the location of a factory is $x$ and the location of a store is $y$, then the cost to transport the computers from $x$ to $y$ can be modeled by the matching between computers to stores, $C(x,y)$. The optimal transport plan ensures that each factory will supply exactly one store and each store will be supplied by exactly one factory and that the overall cost of transporting computers from factories to stores is minimized. This problem is equivalent to finding a minimum weight matching in a bipartite graph. The graph is bipartite because there are $n$ factories and $n$ stores, and the weighted edges between the stores and factories are the costs of moving computers between those nodes.

• Graph Matching Algorithms

• Graphs

• Graph theory

• Hall’s Stable Marriage Problem

• Applications of the Stable Marriage Theorem

1. , R. Matching (graph theory). Retrieved June 19, 2016, from https://commons.wikimedia.org/wiki/File:Matching_(graph_theory).jpg
2. , I. Bipartite graph with matching. Retrieved June 19, 2016, from https://commons.wikimedia.org/wiki/File:Bipartite_graph_with_matching.svg
3. , . Matching (graph theory). Retrieved June 18, 2016, from https://en.wikipedia.org/wiki/Matching_(graph_theory)
4. , M. Maximal-matching.svg. Retrieved June 18, 2016, from https://en.wikipedia.org/wiki/File:Maximal-matching.svg
5. , M. Maximum-matching-labels.svg. Retrieved June 18, 2016, from https://en.wikipedia.org/wiki/File:Maximum-matching-labels.svg
6. , M. Simple-bipartite-graph.svg. Retrieved June 18, 2016, from https://en.wikipedia.org/wiki/File:Simple-bipartite-graph.svg
7. , M. Vertex-cover.svg. Retrieved June 25, 2016, from https://en.wikipedia.org/wiki/File:Vertex-cover.svg
8. , D. Triangulation_3-coloring.svg. Retrieved June 25, 2016, from https://en.wikipedia.org/wiki/File:Triangulation_3-coloring.svg
9. , . Transportation theory (mathematics). Retrieved June 24, 2016, from https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)