Projectile Motion
When first getting a grip on classical mechanics, it is important to digest certain formative examples. One of these examples is that of a projectile: an object that is subject only to the force of gravity. A surprising number of common physical scenarios can be closely modeled with this premise.
Since it is only subject to gravity, the projectile cannot be in contact with any surface. A projectile is always in non-propelled flight, or free-fall. However, this does not mean projectiles always move downward. Consider a classic example: a ball that has been thrown into the air. If it is thrown upward, its motion begins by moving higher, not by falling. But once it is released from the hand throwing it, the ball is only under the influence of gravity, and it is therefore considered a projectile.
Studying projectile motion allows for full application of kinematics, various equations of kinematic-motion and vector geometry.
 A dropped ball will hit the ground at the same time as one flicked horizontally, because vertical motion is independent of horizontal motion.
A dropped ball will hit the ground at the same time as one flicked horizontally, because vertical motion is independent of horizontal motion.
Contents
Examples of Projectile Motion
- A glass accidentally falling off a table.
- A phone tossed into a bed.
- A missile deployed from a military aircraft from level flight.
- A javelin thrown by an athlete.
Assumptions of Projectile Motion
- There is no friction due to air.
- The effect due to the curvature of the earth is negligible.
- The effect due to the rotation of the earth is negligible.
- The entire trajectory is near the surface of the earth.
- For all points of the trajectory, the acceleration due to gravity \(g\) is constant in magnitude \(\big(9.8\text{ m/s}^2\big)\) and direction (toward the earth).
Velocity and Acceleration in Projectile Motion
Consider the diagram shown below. It shows that the velocity of a projectile is changing. Remember that the velocity is always tangential to the path. As the path curves, velocity also changes direction.

When the projectile is in air and air resistance is neglected, the only force acting on it is gravitational force. At all times the acceleration of the particle is constant in magnitude as well as direction, i.e. \(g\) downwards.
Principle of Physical Independence of Motions
Projectile motion is a planar motion in which at least two position coordinates change simultaneously.
Principles of Physical Independence of Motions
- The motion of a projectile is a two-dimensional motion. So, it can be discussed in two parts: horizontal motion and vertical motion. These two motions take place independent of each other. This is called the principle of physical independence of motions.
- The velocity of the projectile can be resolved into two mutually perpendicular components: the horizontal component and the vertical component.
- Acceleration changes velocity. If acceleration in a particular direction is zero, then velocity in that direction remains the same. Thus, in projectile motion, the horizontal component of velocity remains unchanged throughout the flight. The horizontal motion is a uniform motion.
- The force of gravity continuously affects the vertical component, so the vertical motion is a uniformly accelerated motion.
Projectiles can be thrown in various ways: on a level ground, from a high tower to ground, from an aeroplane, etc. The following section discusses some cases in detail.
Oblique Projectiles on Level Ground
In the diagram, a particle is thrown with speed \(u\) at an angle of \(\theta\) with the horizontal.

An analysis of the motion of the projectile starts by breaking the components of initial velocity and acceleration into horizontal (along \(x\)-axis) and vertical (along \(y\)-axis) components. Breaking the velocity and acceleration into independent components helps to study a 2-D projectile motion as two independent 1-D motions.
- The horizontal component of velocity \( {u_x} = u\cos \theta.\)
- The vertical component of velocity \( {u_y} = u\sin \theta. \)
- The horizontal component of acceleration \( {a_x} = 0. \)
- The vertical component of acceleration \( {a_y} = - g. \) (Negative sign shows that the acceleration is in a downward direction.)
Time of Flight
The total time spent in the air is \(T = \frac{{2u\sin \theta }}{g}\).
We have
\[{S_y} = {u_y}t + \frac{1}{2}{a_y}{t^2}.\]
The projectile lands back at the same height, so the displacement in vertical direction is zero:
\[\begin{align} 0 &= u\sin \theta T - \dfrac{1}{2}g{T^2}\\ \Rightarrow T &= \dfrac{{2u\sin \theta }}{g}.\ _\square \end{align}\]
Important Point: The time of flight is independent of the horizontal component of velocity. The faster a projectile is thrown up, the longer it will stay in the air.
Maximum Height
The maximum height a projectile reaches above its release point is \({H_{\max }} = \frac{{{u^2}{{\sin }^2}\theta }}{{2g}}\).
(Avoid this pitfall: The velocity at the highest point in projectile motion is not zero, although the vertical component of velocity is 0.)
For the motion in the vertical direction,
\[v_y^2 = u_y^2 + 2{a_y}{S_y}.\]
At the highest point, the vertical component of velocity is zero:
\[\begin{align} 0 &= {(u\sin \theta )^2} - 2g{H_{\max }}\\ \Rightarrow {H_{\max }} &= \frac{{{u^2}{{\sin }^2}\theta }}{{2g}}.\ _\square \end{align}\]
- The maximum height is independent of the horizontal component of velocity. The faster a projectile is thrown upwards, the higher it will go in an upward direction, i.e. the longer it will resist the downward pull of gravity.
- Both time of flight and maximum height depend on the vertical component of velocity, so the relation between them can be expressed as \(\frac{{{H_{\max }}}}{{{T^2}}} = \frac{g}{8}.\)
Horizontal Range
The net displacement in the horizontal direction for an object with no vertical displacement is \(R = \frac{{{u^2}\sin 2\theta }}{g}.\)
For the motion in the horizontal direction,
\[{S_x} = {u_x}t + \frac{1}{2}{a_x}{t^2}.\]
Acceleration in horizontal direction is zero:
\[\begin{align} R& = (u\cos \theta )T\\ & = (u\cos \theta )\frac{{2u\sin \theta }}{g}\\ & = \frac{{2{u^2}\sin \theta \cos \theta }}{g} \\ &= \frac{{{u^2}\sin 2\theta }}{g}.\ _\square \end{align}\]
- The horizontal range depends upon both the horizontal and vertical components of velocity.
- For a specified speed of projection, the range will max out at an angle of projection equal to \(45^\circ\).
- For projectiles moving at equal speed, the range will be equal when both projectiles have complementary angles of projection.
- The relation between range, maximum height, and time of flight is \(R\tan \theta = \frac{1}{2}g{T^2} = 4H\).
Equation of Trajectory
The equation of the path followed by a projectile is \(y = x\tan \theta \left( {1 - \frac{{gx}}{{{u^2}\sin 2\theta }}} \right).\)
The equation of a curve in two-dimensional space is a relation between \(x\)- and \(y\)-coordinates. By using the equations of motion in the horizontal and vertical directions, respectively, we can find the relations between \(x\) and \(t\) and between \(y\) and \(t.\) Then by eliminating \(t,\) we can find the relationship between \(x\) and \(y.\)
For the motion in the \(x\)-direction,
\[\begin{align} {S_x} &= {u_x}t + \frac{1}{2}{a_x}{t^2}\\ x &= u\cos \theta \ t\\ \Rightarrow t &= \frac{x}{{u\cos \theta }}. \end{align}\]
For the motion in the \(y\)-direction,
\[\begin{align} {S_y} &= {u_y}t + \frac{1}{2}{a_y}{t^2}\\ y &= u\sin \theta \,t - \frac{1}{2}g{t^2}. \end{align}\]
Eliminating \(t\) from the equations,
\[\begin{align} y &= u\sin \theta \frac{x}{{u\cos \theta }} - \frac{1}{2}g{\left( {\frac{x}{{u\cos \theta }}} \right)^2}\\ &= x\tan \theta \left( {1 - \frac{{gx}}{{{u^2}\sin 2\theta }}} \right).\ _\square \end{align}\]
Observe that the equation is in the form of a parabola \(y=ax^2+bx,\) where
\[a=u\tan\theta, \quad b= \dfrac{g}{2u^2\cos^2\theta}.\]
The equation of trajectory can also be written as
\[y = x\tan \theta \left( {1 - \frac{x}{R}} \right),\]
where \(R\) is the horizontal range.
What is the shape of the curve?
As \(y\) depends on the square of \(x,\) the curve must be a parabola. Therefore, when an object is thrown under gravity \((\)at some angle other than \(90^\circ\) to the horizontal plane\(),\) it follows a parabolic path. This also implies that whenever an object moves with constant acceleration with its initial velocity, not in the direction of acceleration, the particle follows a parabolic path.
A particle is thrown from the ground with speed \(20\text{ m/s}\) at an angle of \(30^\circ\) with the horizontal. Find the horizontal range, maximum height, and time of flight of the projectile.
We have
\[\begin{align} R &= \dfrac{{{u^2}\sin 2\theta }}{g}\\ &= \dfrac{{{{(20)}^2}\sin {{60}^0}}}{{10}}\\ &= 20\sqrt{3}\text{ m},\\\\ H &= \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}\\ &= \dfrac{{{{(20)}^2}{{\sin }^2}(30)}}{{2 \times 10}}\\ &= 5\text{ m}, \\\\ T &= \dfrac{{2u\sin \theta }}{g}\\ &= \dfrac{{2 \times 20\sin {{30}^0}}}{{10}} \\ &= 2\text{ s}.\ _\square \end{align}\]
The equation of trajectory of a projectile is \(y = 16x - \frac{{5{x^2}}}{4}\). Find the horizontal range.
The equation of a projectile motion is \(y = x\tan \theta \left[ {1 - \frac{x}{R}} \right].\)
The given equation can be rewritten as \(y = 16x\left[ {1 - \frac{\hspace{3mm} x\hspace{3mm} }{\frac{64}5}} \right].\)
By comparing the above 2 equations, we have \(R = \frac{{64}}{5}=12.8\text{ m}.\ _\square\)
In a projectile motion, which of the following is true about the components of velocity of the system?
Assume the system is a ground projectile.
In a cricket match, a 2-meter-tall pace bowler throws a yorker ball with a horizontal velocity of \(20\text{ m/s}\). The batsman hits the ball with twice the horizontal velocity of the ball at an angle of \({45}^\circ\) with the horizontal. The ball lands just in front of a fielder, who kicks the ball with his foot at an angle of \({30}^\circ\) with the horizontal in such a way that it lands just in front of the foot of the bowler. Find the velocity with which the fielder kicked the ball.

Details and Assumptions:
- The air friction is negligible.
- The positions of the batsman, bowler, and fielder are collinear and the batsman hits the ball in the collinear line.
- The bowler throws the ball by stretching his hand just above the top of his head.
- The bowler does not move from his position after releasing the ball from the crease line.
- Take \(g=10{\text{ m/s}}^2\) the acceleration due to gravity.
- Round your answer \((\)in \(\text{m/s})\) off to the nearest integer.
Ball \(A\) of mass \(1\text{ kg}\) is thrown at an angle of \({45}^\circ\) with the horizontal with kinetic energy \(50\text{ J}\) such that it hits ball \(B\) of the same mass placed on the top of a pole. In this collision, half of the kinetic energy of ball \(A\) at that instant is transferred to ball \(B,\) causing ball \(B\) to move in a forward direction. If it is known that the height at which ball \(B\) was placed is the maximum height that the initial projectile of ball \(A\) would have traveled, then find the distance of the final position of ball \(B\) from the foot of the pole.
The figure below would help in understanding the situation:
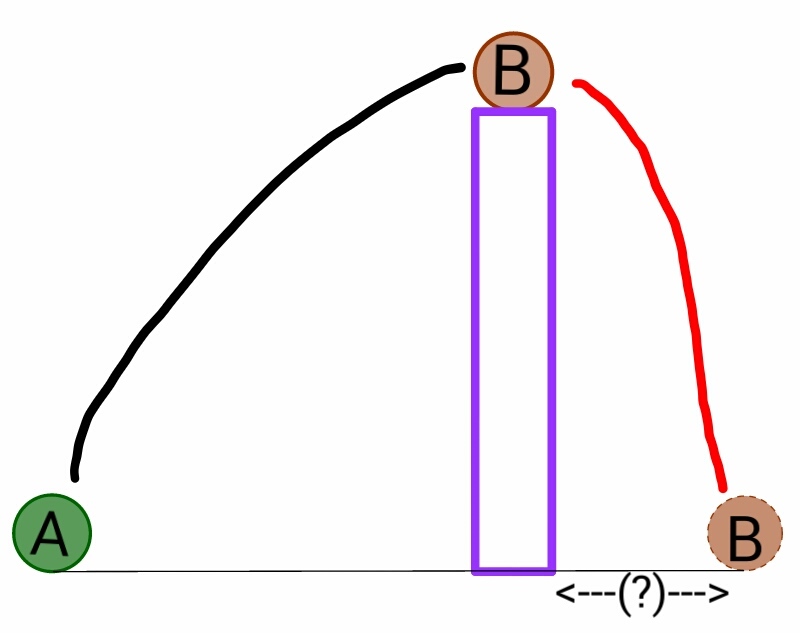
Details and Assumptions:
- Ball \(B\) does not rebound after hitting the ground.
- Air friction is negligible.
- Take \(g=10\text{ m/s}^2\) as the acceleration due to gravity.
- Give your answer (in \(\text{m}\)) to two decimal places.
Projectile from a Height
A projectile is thrown from a tower of height \(h\) horizontally with speed \(u:\)

The horizontal direction is taken as positive, while the vertical, downward direction is taken as negative. The components of initial velocity and acceleration along the \(x\)-axis and \(y\)-axis will be as follows:
- initial velocity along the \(x\)-axis: \({u_x} = u\)
- initial velocity along the \(y\)-axis: \({u_y} = 0\)
- acceleration along the \(x\)-axis: \( 0\)
- acceleration along the \(y\)-axis: \( +g.\)
Time of Flight:
For the motion in the \(y\)-direction, we have
\[{S_y} = {u_y}t + \frac{1}{2}{a_y}{t^2}.\]
Finally, the particle lands on ground and travels distance \(h\) (equal to the height of tower) in vertically downward direction. Therefore, the displacement in the \(y\)-direction is \({S_y} = h,\) so
\[h = \dfrac{1}{2}g{T^2}\implies T= \sqrt {\dfrac{{2h}}{g}}.\]
Horizontal Range:
For the displacement in the horizontal direction, we have
\[\begin{align}
{S_x} &= {u_x}t + \dfrac{1}{2}{a_x}{t^2}\\
R &= uT\\
&= u\sqrt {\dfrac{{2h}}{g}}.
\end{align}\]
A ball rolls off the top of a staircase with a horizontal velocity of \(u\text{ m/s}.\) If the steps are \(h\) meters high and \(b\) meters wide, the ball will just hit the edge of the \(n^\text{th}\) step. What is \(n?\)

If the ball hits the \(n^\text{th}\) step, then the displacement in the vertical, downward direction will be \(nh\) and the displacement in the horizontal direction will be \(nb.\) Therefore,
\[\begin{align} R &= u\sqrt {\dfrac{{2h}}{g}}\\ nb &= u\sqrt {\dfrac{{2nh}}{g}} \\ \Rightarrow n &= \dfrac{{2{u^2}h}}{{{b^2}g}}.\ _\square \end{align}\]
A body is projected horizontally from the top of a tower with initial velocity \(18\text{ m/s}.\) If it hits the ground at angle \(45^\circ,\) what is its vertical component of velocity when it strikes the ground?

As the projectile hits the ground at angle \({45^\circ},\)
\[\tan {45^\circ} = \frac{{{v_y}}}{{{v_x}}}.\]
The vertical and horizontal components of velocity are equal and the horizontal component of velocity always remains the same, so
\[{v_y} = {v_x} = 18\text{ m/s}.\ _\square\]

Two bullets of equal masses are fired horizontally with speeds of 10 m/s and 20 m/s from the same height at the same time. Which bullet will hit the ground first?
Neglect air resistance, the curvature of the earth, lift effects on the bullet, etc.

A ball of mass \(2 \text{ kg}\) is placed in front of a spring having constant \(20 \text{ N/m}\) and compression \(20 \text{ m}\) at a height of \(100 \text{ m}\) above the ground.
Now, the spring is released, giving the ball a horizontal velocity.
Find the total displacement (in meters) of the ball from the spring when it hits the ground.
Details and Assumptions:
- The ball does not rebound after hitting the ground first.
- Air friction is negligible.
- The spring is 100% efficient.
- Take \(g=10 {\text{ m/s}}^2\) as the acceleration due to gravity.