Proof by Contradiction

Proof by contradiction (also known as indirect proof or the method of reductio ad absurdum) is a common proof technique that is based on a very simple principle: something that leads to a contradiction can not be true, and if so, the opposite must be true. It's a principle that is reminiscent of the philosophy of a certain fictional detective:

"When you have eliminated the impossible, whatever remains, however improbable, must be the truth."

"Sherlock Holmes" in the novel The Sign of the Four (1890) by Sir Arthur Conan Doyle

To prove a statement by contradiction, start by assuming the opposite of what you would like to prove. Then show that the consequences of this premise are impossible. This means that your original statement must be true.

Prove that there is no largest number.

---

Suppose that a largest number does exist. Let it be $L.$ If $L$ really is the largest number, then there can be no number larger than $L.$

Consider the number $L+1.$ This number is larger than $L,$ but it was just stated that there cannot be any number larger than $L$. This is a contradiction. The premise that there existed a largest number cannot be true, because the consequence of this premise is absurd. Therefore, there is no largest number. $_\square$

G. H. Hardy called proof by contradiction "one of a mathematician's finest weapons," saying, "It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game."

Contradiction proofs are often used when there is some binary choice between possibilities:

• $\sqrt{2}$ is either rational or irrational.

• There are infinitely many primes or there are finitely many primes.

• Either a line tangent to a circle is perpendicular to the radius of the circle containing the point of tangency, or it is not.

When writing a proof by contradiction, you need to have an idea about which possibility is correct.

• One suspects that $\sqrt{2}$ is irrational, because there doesn't seem to be any rational number that, when squared, equals 2.

• One suspects that there are infinitely many primes, because although they are rare, one can always seem to find more.

• One suspects that a line tangent to a circle is always perpendicular to the radius, because it always seems that way when it is drawn.

Proof by Contradiction Process

• Negate the conclusion: Begin with the premise that whatever you are attempting to prove, the opposite is true. In the introduction example, the goal was to prove that there is no largest number, so the proof begins with the premise that there is a largest number.

• Analyze the consequences of this premise: This step involves putting that premise in some mathematical form. In the introduction example, the largest numbers was given a name, $L.$ It's not necessary to find a specific value for $L;$ it's sufficient to show that it exists in some form.

• Look for a contradiction: A contradiction is something that doesn't make sense given the negated conclusion premise. In the introduction example, a number was found that was larger than $L$. This goes against the premise that $L$ is the largest number.

As soon as a contradiction is found, the proof is complete. You can conclude that what you were trying to prove was correct.

Proof by contradiction isn't very useful for proving formulas or equations. Proof by contradiction needs a specific alternative to whatever you are trying to prove. For example, you wouldn't use proof by contradiction to prove the quadratic formula. There isn't any specific alternative equation to the quadratic equation, so proof by contradiction doesn't help to prove it.

However, proof by contradiction can sometimes be used to prove the converse of a formula or equation. The proof of the converse of the Pythagorean theorem is an example of this.

Proof by contradiction is common in number theory because many proofs require some kind of binary choice between possibilities.

Prove that $\sqrt{2}$ is irrational.

---

Suppose that $\sqrt{2}$ is rational. If it were rational, it could be expressed as the ratio of two co-prime integers $p$ and $q$. Since $p$ and $q$ are co-prime, both of them can not be even.

If $\sqrt{2}=\dfrac{p}{q}$, then $2q^2=p^2$. Since the left hand side is even, so is the right hand side. By Euclid's lemma, $p$ must be even.

If $p$ is even, $p^2$ is a multiple of $4$. This in turn means $2q^2$ is a multiple of $4.$ In other words, $q^2$ is a multiple of $2$. By the same reasoning as above, we conclude that $q$ is even.

That's a contradiction! It was stated that both $p$ and $q$ can't be even.

Assuming that $\sqrt{2}$ is rational led to a contradiction. This means $\sqrt{2}$ can't be rational. We've proved that $\sqrt{2}$ is irrational. $_\square$

Prove that there is no least positive rational number.

---

Suppose that there is a least positive rational number. Call it $k$.

$\frac{k}{2}$ is a positive rational strictly less than $k$. But this contradicts $k$ being the smallest positive rational number. $k,$ in fact, does not exist. In other words, there is no such thing as the least positive rational. $_\square$

Note: This result gives an intuition that any dense subset of $\mathbb{R}$ cannot have a least positive element.

Prove that there are infinitely many prime numbers.

---

Suppose that there are finitely many prime numbers. Then it would be possible to list all of the prime numbers, in order:

$\text{{the set of all prime numbers}}=\{p_1,p_2,p_3,\cdots,p_{n-1},p_{n}\},$

where $p_1<p_2<p_3<\ldots<p_{n-1}<p_n$.

Now consider the product of all of those prime numbers:

$p_1p_2p_3 \cdots p_{n-1}p_n.$

This number is divisible by all of the prime numbers. Now, add 1 to this number:

$p_1p_2p_3 \cdots p_{n-1}p_n+1.$

This number is not divisible by any of the prime numbers, because dividing it by any prime always results in a remainder of $1.$

This implies that this number is a prime number. However, this number is larger than $p_n.$ This contradicts the assertion that $p_n$ is the largest prime number.

Therefore, there is no largest prime number. There are infinitely many prime numbers. $_\square$

Prove that the sum of a rational number and an irrational number is irrational.

---

Suppose that the sum of a rational number and an irrational number is rational. The first rational number can be expressed as $\frac{p}{q},$ where $p$ and $q$ are co-prime integers. Let the irrational number be $a.$ Their sum can be expressed as $\frac{r}{s},$ where $r$ and $s$ are co-prime integers. Then,

$\frac{p}{q}+a=\frac{r}{s}.$

Subtracting $\frac{p}{q}$ from both sides of this equation gives

$\begin{aligned} a &= \frac{r}{s}-\frac{p}{q} \\ \\ &= \frac{qr-ps}{qs}. \end{aligned}$

$qr-ps$ is an integer, and so is $qs.$ Therefore, $a$ is a rational number. However, $a$ was defined to be irrational. This is a contradiction.

Hence, the sum of a rational number and an irrational number is irrational. $_\square$

If $a$, $b$ and $c$ are all odd integers, prove that $ax^2+bx+c=0$ can't have a rational solution.

---

Assume that a rational number $\frac{p}{q}$ is the solution to $ax^2+bx+c=0,$ with $p$ and $q$ co-prime. As with a previous example, this means that both of $p$ and $q$ can't be even. At least one of them has to be odd.

If $\frac{p}{q}$ is indeed a solution to the quadratic, then

$\begin{aligned} a\left(\frac{p}{q}\right)^2+b\frac{p}{q}+c&=0\\ ap^2+bpq+cq^2&=0. \end{aligned}$

Now the right hand side is even, so the left hand side has to be even too. But since $a$, $b$, $c$ are all odd, that can happen only if both $p$ and $q$ are even, and it was made very clear that they are not.

Therefore, a rational number $\frac{p}{q}$ can't be a solution to $ax^2+bx+c=0$ if $a$, $b$ and $c$ are all odd. $_\square$

Prove that the harmonic series diverges.

The harmonic series is

$\sum\limits_{k=1}^\infty{\frac{1}{k}}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\cdots.$

---

Suppose that the harmonic series converges, and consider the following series:

${\large\sum\limits_{k=1}^\infty{2^{-\left\lceil\log_2{k}\right\rceil}}}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\cdots,$

where the $\lceil \ \rceil$ grouping symbols denote the ceiling function.

Each term in this sequence is positive and less than or equal to the corresponding term in the harmonic series:

$\text{For any positive integer }k, \ 0<2^{-\left\lceil\log_2{k}\right\rceil} \le \frac{1}{k}.$

Then if the harmonic series converges, this series converges as well.

However, this series does not converge. Grouping the like terms gives a repeated sum of $\frac{1}{2}:$

${\large\sum\limits_{k=1}^\infty{2^{-\left\lceil\log_2{k}\right\rceil}}}=1+\frac{1}{2}+\underbrace{\frac{1}{4}+\frac{1}{4}}_{\frac{1}{2}}+\underbrace{\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}}_{\frac{1}{2}}+\cdots.$

The fact that this series diverges is a contradiction. Therefore, the harmonic series diverges. $_\square$

When contradiction proofs are used for geometry, it often leads to figures that look absurd. This is to be expected, because a proof by contradiction always begins with a premise that goes against what is believed to be true.

Prove that a line tangent to a circle is perpendicular to the radius of the circle that contains the point of tangency.

---

We are given circle $\text{O},$ tangent line $m,$ and point of tangency $\text{A}.$

Suppose that the tangent line is not perpendicular to the radius containing the point of tangency. Then there exists some other point, $\text{B}$ on line $m$ such that $\overline{\text{OB}}\perp m.$

Since $\text{A}$ is the point of tangency, $\text{B}$ must be outside of the circle. Therefore, $\text{OB}>\text{OA}.$

However, $\Delta \text{OBA}$ is a right triangle, and $\overline{\text{OA}}$ is the hypotenuse of this triangle. Therefore, $\text{OA}>\text{OB}.$ This contradicts the previous assertion that $\text{OB}>\text{OA}.$

Therefore, a line tangent to a circle is always perpendicular to the radius of the circle that contains the point of tangency. $_\square$

Given the Pythagorean theorem, prove the converse of the Pythagorean theorem. That is, if a triangle contains side lengths $a,$ $b,$ and $c$ such that $a^2+b^2=c^2,$ then the triangle is a right triangle.

---

Suppose that there exists a triangle with $a^2+b^2=c^2$ that is not a right triangle. The triangle can either be acute or obtuse.

Assume that the triangle is acute.

Let point $\text{D}$ be the point such that $\text{CD}=b$ and $\angle BCD = 90^\circ .$

$\Delta BCD$ is a right triangle with side lengths $a$ and $b$. It is given that $a^2+b^2=c^2,$ so by the Pythagorean theorem, $BD=c.$

Note that $\Delta ABD$ and $\Delta ACD$ are isosceles triangles. Thus, $\angle ADB \cong \angle DAB$ and $\angle ADC \cong \angle DAC.$

It is also apparent that $\angle DAB>\angle DAC$ and $\angle ADC > \angle ADB.$ However, this cannot be true given the previous assertion about congruent angles.

A similar contradiction arises if one assumes that the triangle is obtuse.

Thus, if a triangle has side lengths $a,$ $b,$ and $c$ such that $a^2+b^2=c^2,$ then the triangle is a right triangle. $_\square$

Euclid's Elements, Book 1, Proposition 6. Prove that if two angles of a triangle are congruent, then the sides opposite them are congruent.

Note: This proof is the converse of Proposition 5 (If two sides of a triangle are congruent, then the angles opposite them are congruent), and it also follows from Proposition 4 (SAS congruence). There are other ways to prove this theorem, but this proof is notable for requiring very few prerequisite propositions.

---

Suppose that there exists a triangle with two congruent angles, but the sides opposite those angles are not congruent. If the sides are not congruent, then one of them must be longer.

In the triangle above, $\angle A \cong \angle C$ and $AB>BC.$

Since $\overline{AB}$ is longer than $\overline{BC},$ let $D$ be placed on $\overline{AB}$ such that $AD=BC.$

Now these congruences can be observed:

• $\overline{AD} \cong \overline{BC},$ which is given by how point $D$ was defined.
• $\angle A \cong \angle ACB,$ also given.
• $\overline{AC} \cong \overline{AC},$ by the reflexive property of congruence.

These congruences suggest that $\Delta ABC \cong \Delta CDA$ by SAS triangle congruence. However, this cannot be true, because $\Delta ABC$ is clearly larger.

Hence, if two angles of a triangle are congruent, then the sides opposite them are congruent. $_\square$

Pigeonhole Principle:
5 points are placed within a unit equilateral triangle. Prove that two of those points must be a maximum distance of $\frac{1}{2}$ from each other.

---

Suppose that for any pair of points among the 5, the distance between the points is greater than $\frac{1}{2}$. Now consider the partition of the triangle into 4 smaller equilateral triangles.

Note that the maximum distance between two points within one of these smaller triangles is $\frac{1}{2}.$ A point could be placed within each of the triangles (the 4 blue points) such that each point is further than $\frac{1}{2}$ from the other points. However, the $5^\text{th}$ point (the red one) would have to be placed within the same triangle as another point.

Thus, if 5 points are placed within a unit equilateral triangle, two of those points must be at most $\frac{1}{2}$ away from each other. $_\square$

Ramsey's Theorem:
Prove that out of a party of 6 people, there exists a group of 3 mutual friends or a group of 3 mutual non-friends.

---

Suppose that given any group of 3 people among the 6, there are at most 2 friendships or 2 non-friendships. Let the 6 people be labeled with $\text{A},$ $\text{B},$ $\text{C},$ $\text{D},$ $\text{E},$ and $\text{F}.$ The possible relationships are shown with dashed lines below.

Begin with person $\text{A}.$ Suppose that $\text{A}$ is friends with at least 3 people, and suppose 3 of those people are $\text{B},$ $\text{C},$ and $\text{D}.$

Let a friendship be denoted with a blue line, and let a non-friendship be denoted with a red line. If any pair of $\text{B},$ $\text{C},$ or $\text{D}$ are friends, then they form a group of 3 mutual friends with $\text{A}.$

If $\text{B},$ $\text{C},$ and $\text{D}$ are all non-friends, then they form a group of 3 mutual non-friends.

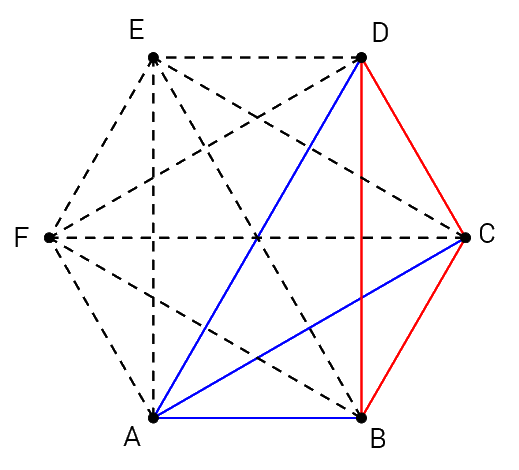
Without loss of generality, this same contradiction arises with any combination of 4 people including $\text{A}.$

When you consider what happens when $\text{A}$ has at least 3 non-friends among the group, a similar contradiction arises. Note that $\text{A}$ must have at least 3 friends or have at least 3 non-friends.

Therefore, given any party of 6 people, there exists a group of 3 mutual friends or a group of 3 mutual non-friends. $_\square$

Graph Theory:
Prove that it is impossible to traverse the following graph by traveling along each path exactly once. Any of the vertices may be selected as the starting vertex or ending vertex, and vertices may be passed more than once.

---

Suppose that it is possible to traverse the graph by traveling along each path exactly once. Consider how many times each vertex would be passed through. For every time a vertex is entered, it is also exited. Therefore, if each path is traveled exactly once, then each vertex should have an even number of paths coming from it. The exceptions to this are the starting vertex and ending vertex. These vertices should have an odd number of paths coming from them. There can only be one starting vertex and one ending vertex. However, the graph above has 4 vertices with an odd number of paths coming from them.

Thus, it is impossible to traverse the above graph by traveling along each path exactly once. $_\square$

Hall's marriage theorem is often used in problems that require matchmaking between elements in a set. Its application in the following problem isn't entirely obvious, but consider this: in order for a $1\times 2$ domino to be placed in the figure, a white tile must be "matched" with an adjacent blue tile.

Main Article: Fermat's Method of Infinite Descent

Fermat's method of infinite descent is a special kind of proof by contradiction. It is based on the fact that there exists a smallest positive integer, $1$. If a premise leads to infinitely many positive integer solutions such that each solution is successively smaller, then this is a contradiction.

Prove that if $k$ is a positive integer and $\sqrt{k}$ is not an integer, then $\sqrt{k}$ is irrational.

---

Suppose that $\sqrt{k}$ is rational. Then it can be expressed as $\frac{p}{q}$, where $p$ and $q$ are positive co-prime integers. Let $n$ be the largest integer that is less than $\sqrt{k}$, then $\sqrt{k}-n$ is a positive number that is less than $1:$

$\begin{aligned} \sqrt{k} &= \frac{p}{q} \\ &= \frac{p\left(\sqrt{k}-n\right)}{q\left(\sqrt{k}-n\right)} \\ &= \frac{p\sqrt{k}-pn}{q\sqrt{k}-qn}. \end{aligned}$

Note that the above expression is equivalent to $\sqrt{k},$ but the numerator and denominator are each smaller than $p$ and $q$, respectively, because $\sqrt{k}-n$ is less than $1.$

Substitute $p=q\sqrt{k}$ into the numerator and $\sqrt{k}=\frac{p}{q}$ into the denominator:

$\begin{aligned} \sqrt{k} &= \frac{q\sqrt{k}\sqrt{k}-pn}{q\left(\frac{p}{q}\right)-qn} \\ &= \frac{qk-pn}{p-qn}. \end{aligned}$

Recall that $k,$ $p,$ $q,$ and $n$ are integers. Also recall that the numerator of the above expression is positive and less than $p,$ and likewise the denominator of the above expression is positive and less than $q.$ This implies that there exist positive integers $p'$ and $q'$ such that

$\begin{aligned} p'&=qk-pn, \ \, p'<p\\\\ q'&=p-qn, \ \, q'<q\\\\ \sqrt{k}&=\frac{p'}{q'}. \end{aligned}$

The process above could be repeated indefinitely to produce positive integers $p^*$ and $q^*$ that are successively smaller after each step. However, there exists a smallest positive integer, $1.$ This is a contradiction, because one would not be able to indefinitely find smaller positive integers if a smallest positive integer exists.

Hence, if $k$ is a positive integer and $\sqrt{k}$ is not an integer, then $\sqrt{k}$ is irrational. $_\square$