Edge Cover
An edge cover of a graph \(G\) is a set of edges \(E_c\) where every vertex in \(G\) is incident (touching) with at least one of the edges in \(E_c\). This means that each node in the graph is touching at least one of the edges in the edge covering. Edge cover is a topic in graph theory that has applications in matching problems and optimization problems . An edge cover might be a good way to solve a problem if the answer needs to include all nodes of a graph.
Many times, themes from edge covering are adapted and integrated into other problems. Ideas from edge cover are seen in spanning trees, minimum spanning trees, edge coloring, and the clique problem — all are very useful topics in computer science due to their applications in shortest-path finding algorithms, flow network algorithms, and more abstract problems in computability and complexity theory.
Edge Cover
An edge cover of a graph \(G\) is a set of edges \(E_c\) where every vertex in \(G\) is incident with at least one of the edges in \(E_c\). This means that each node in the graph is touching at least one of the edges in the edge covering.
In the image below, the red edges represent the edges in the edge cover of the graph.
 Edge covering[1]
Edge covering[1]
Say you are going on a road trip, and there are five cities you want to visit. The cities are connected via roads. If this situation were modeled as a graph, what would the edges and nodes be?
The nodes would be the cities and the edges would be the roads.How does edge cover apply to finding a route that will take you to each city?
Since edge cover involves finding a set of edges that will touch each node, and we want to go to each node (city), using edge cover, we can determine the roads to take (edges) that will bring us to each city.
Minimum Edge Cover
A minimum edge covering is an edge covering using the smallest possible number of edges. In the graphs below, the minimum edge covering is indicated by red edges. The edge covering number is is the size of the smallest edge cover of \(G\) and is denoted by \(\rho(G)\). If any of the red edges were deleted from the edge covering, there would be vertices not connected to the edge covering, making the edge coloring invalid.
Edge cover is a type of optimization problem that can be solved in polynomial time.
Say you are having a party, but your guests are very picky eaters. You have the following list detailing which foods each guest will and will not eat.
Name Food William Pizza, Rice, Apples Emma Potatoes, Rice, Peas Ray Cheese, Apples, Steak Robert Pizza Katherine Peas, Cheese Vivian Cheese, Potatoes Divya Apples You want to minimize the number of groceries you buy while still making sure that each guest will have at least one food item that he or she will eat. You think that this problem can be solved using a edge cover (possibly slightly modified). What does the graph look like? Which foods should you buy?
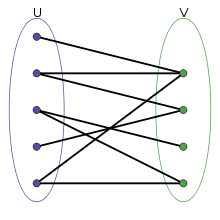
Try a bipartite graph!Here's an example of a bipartite graph that might give you some ideas.
Here, we really only care that each person has a food they will eat. We don't care if we don't have every food item that each person likes. The only requirement is that each person have at least one food item. While we can use a bipartite graph to help show each person's food preferences, the only nodes we will be using in our covering are the nodes indicating the people. That is, our edge cover need only connect each person node with some food item node — there must be at least one edge per person.Here is one way to model this as a graph.
 Of course a trivial solution to this problem would be to add all of the edges into the edge cover — buy all of the food so everyone is sure to be happy. But this is not optimal for minimizing the number of items you must buy. Here is one configuration that minimizes the number of items you have to buy (there are a few optimal solutions).
Of course a trivial solution to this problem would be to add all of the edges into the edge cover — buy all of the food so everyone is sure to be happy. But this is not optimal for minimizing the number of items you must buy. Here is one configuration that minimizes the number of items you have to buy (there are a few optimal solutions).

A perfect matching is also a minimum edge cover. This means that the size of a maximum matching cannot be larger than the size of a minimum edge cover.
Matching
Matching is a particular, is a type of altered edge cover. A matching in a graph is a set of edges that do not have a set of common vertices. In other words, a matching is a graph where each node has only one edge coming from it. This means that a matching doesn't necessarily have to include all nodes or edges.
Here is an example of a matching graph (the matching is indicated by red edges) that is not an edge covering.
What single edge can you color red to make this matching into an edge cover?
The added edge is colored blue.

Together, the red and blue edges form an edge cover because every vertex in the graph is connected to one of those edges.
A maximum matching is a matching that contains the largest possible number of edges (and therefore, as many vertices are matched as possible). In other words, a maximum matching is the maximal matching with the maximum number of edges. Every maximum matching is maximal, but not every maximal matching is a maximum matching.
A maximum matching is different from edge cover, but the two concepts are closely related. In the graph below, the red edges indicate a maximum matching and blue edges are added to show the edges that need to be added to the maximum matching in order to complete the edge cover set of edges.
The graph on the right is both a maximum matching and an edge cover since all of the lines in the matching (indicated by the red edges) touch all of the vertices in the graph. The graph on the left, however, needs some additional edges (the blue ones) to be added to its maximum matching in order to become an edge cover.
Finding An Edge Covering
An edge covering can be found in polynomial time by finding a maximum matching and extending it using a greedy algorithm until all vertices are covered by the edges in the edge cover set.
Applications
The topics listed below have more constraints than just edge covering, but do use ideas present in edge covering in their problem approaches.
Minimum Spanning Trees
A spanning tree is a subgraph in a graph that has several properties.I think what would make your statement clearer is: First, if T is a spanning tree of graph G , then T must contain every vertex in G and T must be said to connect each vertex with a continuous path of edges. This has elements of edge cover because every vertex in G must be in T , and because the edges of T touch every vertex at least once they would then represent an edge cover.
Here is a set of examples of spanning trees.
Spanning trees are important in path-finding algorithms such as Dijkstra's shortest path algorithm and A* search algorithm. Spanning trees are calculated as sub-parts in those algorithms. It is also used in network routing protocols. The spanning tree protocol is one example.
Minimum spanning trees are a variant of the spanning tree. A minimum spanning tree for an unweighted graph, G, is a spanning tree that minimizes the number of edges or edge weights. A minimum spanning tree for a weighted graph, G, is a spanning tree that minimizes the weights of the edges in the tree.
Minimum spanning trees are very helpful in many applications and algorithms. They are often used in water networks, electrical grids, and computer networks. They are also used in graph problems like the traveling salesperson problem, and they are used in important algorithms such as the min cut max flow algorithm.
Here is a minimum spanning tree, indicated by the thicker black line, in the overall graph.
This path connects all the vertices together using the shortest length. The sum of the lengths of each edge for this spanning tree is smaller than the sum of any other other possible spanning trees.
Graph Coloring
A coloring on a graph can involve it's edges or it's vertices . Many day-to-day problems, like minimizing conflicts in scheduling, are also equivalent to graph colorings.
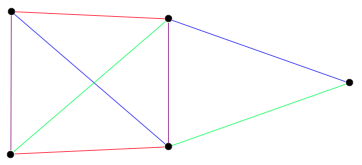 A proper edge coloring with 4 colors
A proper edge coloring with 4 colors
The most common type of edge coloring is analogous to graph (vertex) colorings. Each edge of a graph has a color assigned to it in such a way that no two adjacent edges are the same color (this is an augmenting path). Such a coloring is a proper edge coloring. With cycle graphs, the analogy becomes an equivalence, as there is an edge-vertex duality. In general, however, the chromatic number is not related to the minimal \(k\) such that a proper edge \(k\)-coloring exists.
Another type of edge coloring is used in Ramsey Theory and similar problems. In such cases, edges of the graph are colored one of \(k\) colors and mathematicians investigate the resulting colored graph substructures to determine what sizes of complete subgraphs exist.
A final type of edge coloring is used in the study of spanning trees. Edges are colored in such a way that there does not exist a cycle of the same color, and the minimal number of colors required for such an edge coloring of a given graph is known as its arboricity.
References
- , M. Edge-cover.svg. Retrieved July 3, 2016, from https://en.wikipedia.org/wiki/File:Edge-cover.svg
- , M. Minimum-edge-cover.svg. Retrieved July 3, 2016, from https://en.wikipedia.org/wiki/File:Minimum-edge-cover.svg
- , M. Simple-bipartite-graph.svg. Retrieved June 18, 2016, from https://en.wikipedia.org/wiki/File:Simple-bipartite-graph.svg
- , B. . Retrieved July 4, 2016, from http://math.stackexchange.com/questions/933988/cubic-3-edge-connected-graph-has-edge-cover-that-can-omit-2-3-of-all-edges-over
- , I. Bipartite graph with matching. Retrieved June 19, 2016, from https://commons.wikimedia.org/wiki/File:Bipartite_graph_with_matching.svg
- , M. Minimum-edge-cover-from-maximum-matching.svg. Retrieved July 3, 2016, from https://en.wikipedia.org/wiki/File:Minimum-edge-cover-from-maximum-matching.svg
- , Q. File:Spanning Trees qtl1.svg. Retrieved July 5, 2016, from https://commons.wikimedia.org/wiki/File:Spanning_Trees_qtl1.svg
- , D. Minimum spanning tree.svg. Retrieved July 5, 2016, from https://en.wikipedia.org/wiki/File:Minimum_spanning_tree.svg