Pairing Heap
Pairing heaps are a specific implementation of the heap data structure. They have fast amortized running times for their operations. Pairing heaps are a type of self-adjusting binomial heap. Self-adjusting structures rearrange themselves when operations happen to remain balanced, for example, an AVL tree is an example of a self-adjusting or rebalancing binary search tree.
Though pairing heaps are very simple to implement, they can be difficult to analyze. In fact, finding the exact bounds on the running time of pairing heap operations is still an open problem[1], but the current best guesses for running times are listed in the complexity section.
Pairing heaps are used in algorithms associated with minimum spanning trees, and like other heaps, pairing heaps can be used to implement priority queues.
Contents
Structure of a Pairing Heap
A pairing heap can be (a) an empty heap or (b) a root and a list of pairing heaps (which may be empty). Pairing heaps maintain a min-heap property that all parent nodes always have a smaller value than their children (and maintains the max-heap property if the pairing heap is a max heap).
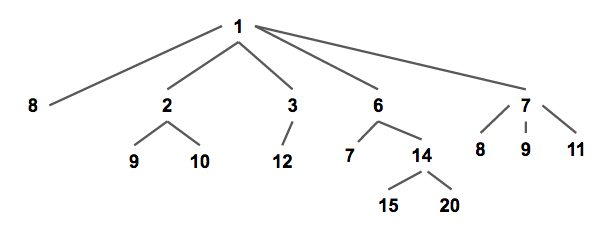
Each node keeps track of the following information: a pointer to its leftmost child node and pointers to its sibling nodes. The pointers in the pairing heap shown above look like this.

Minimum Functionalities
Here is how pairing heaps implement the basic functionalities of heaps and the time complexity of each operation. These operations describe a min pairing heap, but could be easily rearranged to work for max pairing heaps.
Find Minimum
In a pairing heap, finding the minimum element is very simple — just return the top element of the heap.
Here is pseudocode describing this operation.[2]
1 2 3 4 5 | |
Merge
If merging occurs between a non-empty pairing heap and an empty pairing heap, merge just returns the non-empty pairing heap. If both pairing heaps are non-empty, the merge function returns a new heap where the smallest root of the two heaps is the root of the new combined heap and adds the other heap to the list of sub-heaps.
](https://ds055uzetaobb.cloudfront.net/brioche/uploads/tGArb9KgZO-mergeabpairfina.png?width=1200) Inspired by this
Inspired by this
Here is pseudocode describing this operation.[2]
1 2 3 4 5 6 7 8 9 | |
Extract Minimum
In a min heap, the minimum element is the root of the heap. To delete this element, delete the root node. If the root had two or more subtrees, these must be merged together into a single tree. Because there are no parent pointers, it is more difficult to tell if a deletion will cause a heap property violation (unlike in other heap implementations). There are many ways to check if a heap violation is caused, but the simplest is called a two-pass pairing or a two-pass merge. On the first pass, the two-pass pairing moves left to right merging pairs of trees, and on the second pass, it moves right to left and merges the rightmost subtree with the remaining subtrees, one tree at a time. Two-pass pairing was inspired by splay trees.
These images show how the two-pass merge works.
](https://ds055uzetaobb.cloudfront.net/brioche/uploads/EPiOJWdnxK-pass1.png?width=1200) Inspired by this
Inspired by this
](https://ds055uzetaobb.cloudfront.net/brioche/uploads/mBBY5uj9lA-pass2.png?width=1200) Inspired by this
Inspired by this
Here is pseudocode describing this operation.[2]
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
Insert
Inserting an element is like merging the element with the heap.
Here is an example where the added node does not violate the min-heap property.
](https://ds055uzetaobb.cloudfront.net/brioche/uploads/aowLdvcH7g-insert3pair.png?width=1200) Inspired by this
Inspired by this
Here is an example where the inserted node does violate the min-heap property (since it is smaller than the root), and must become the root.
](https://ds055uzetaobb.cloudfront.net/brioche/uploads/1zpTW0Hjla-insert1pair.png?width=1200) Inspired by this
Inspired by this
Here is pseudocode describing this operation.[2]
1 2 | |
Remove
To delete a node \(n\), detach the subtree that is rooted at node \(n\). Then, delete \(n\) from the tree and merge its subtrees into one subtree using a two-pass method (as described in the extract-min section). Merge the detached subtree with the subtree resulting from the two-pass.
Let's say we want to delete the root node, \(1\), from this pairing heap. We will think about the heap in terms of its pointers.[3]
The starting heap.

After we remove \(1\), \(8\), \(2\), \(3\), \(6\), and \(7\) are no longer siblings. So remove the pointer from \(1\) to \(2\), and then remove the sibling points between \(8\), \(2\), \(3\), \(6\), and \(7\).

The passings occur.


And finally, they are merged together.

Decrease Key
To decrease the key of node \(n\), if \(n\) is already the root or if \(n\) is a new key that is greater than or equal to its parent, no additional steps are needed. If \(n\) is a new key and is less than the value of its parent, to maintain the min-heap property, action must be taken to produce a valid heap.
In pairing heaps, the corrective action is as follows.
Remove the subtree rooted at \(n\)
Merge the resulting two trees together
Implementation
Here is a pseudocode implementation of pairing heaps.[4]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | |
Python implementations of pairing heaps can be quite long, but here are a few examples of Python pairing heaps: here, here, and here.
Summary of the Running Times of Pairing Heaps
Here is a table[5] describing the amortized running times of operations on pairing heaps.
| Operation | Actual Running Time | Amortized Running Time |
| Insert | \(O(1)\) | \(O(1)\) |
| Remove | \(O(n)\) | \(O(\log n)\) |
| Find Min | \(O(1)\) | \(O(1)\) |
| Extract Min | \(O(n)\) | \(O(\log n)\) |
| Decrease Key | \(O(1)\) | \(O(\log n)\) |
| Merge | \(O(1)\) | \(O(\log n)\) |
In practice, pairing heaps are faster than binary heaps and Fibonacci heaps.[2]. Many studies have shown pairing heaps to perform better than Fibonacci heaps in implementations of Dijkstra’s algorithm and Prim’s minimum spanning tree algorithms.[5]
See Also
References
- Fredman, M., Sedgewick, R., Sleator, D., & Tarjan, R. The Pairing Heap: A New Form of Self-Adjusting Heap. Retrieved June 7, 2016, from https://www.cs.cmu.edu/~sleator/papers/pairing-heaps.pdf
- , . Pairing Heaps. Retrieved June 7, 2016, from https://en.wikipedia.org/wiki/Pairing_heap
- Allan , S. Merging Priority Queues . Retrieved July 3, 2016, from http://digital.cs.usu.edu/~allan/DS/Notes/Ch23.pdf
- Fredman , M. Binomial, Fibonacci, and Pairing Heaps. Retrieved June 7, 2016, from http://web.onda.com.br/abveiga/capitulo7-ingles.pdf
- , . Priority Queues. Retrieved June 7, 2016, from http://www.uqac.ca/azinflou/Fichiers840/pairing.pdf