Pi

\(\pi\) is the ratio between a circle's circumference and diameter. That is,
\[\dfrac{\text{circumference}}{\text{diameter}}=\pi.\]
\(\pi\) is a fundamental constant in mathematics, especially in geometry, trigonometry, and calculus. The first 10 digits of \( \pi\) (sometimes written as "pi" and pronounced as "pie") are \(3.141592653...\), but any finite list of digits is an approximation of \(\pi\). This is because \( \pi\) is an irrational number \(\big(\)meaning it is not perfectly equivalent to any ratio of whole numbers, \(\frac{a}{b}\big),\) as well as a transcendental number.
Contents
- Applications of \( \pi\) in Geometry
- Approximating \( \pi\) using Polygons
- Approximating \( \pi\) by Statistical Techniques
- Applications of \( \pi\) in Complex Numbers, Trigonometry, and Euler's Formula
- Exactly Defining \( \pi\) as an Infinite Series
- Exactly Defining \(\pi\) as an Integral
- More Digits
Applications of \( \pi\) in Geometry
Common geometric formulae involving \(\pi:\)
- \(\pi = \frac{C}{d}, \) where \(C\) is the circumference of a circle and \(d\) is the diameter.
- \(A = \pi r^2, \) where \(A\) is the area of a circle and \(r\) is the radius.
- \(V = \frac{4}{3}\pi r^3, \) where \(V\) is the volume of a sphere and \(r\) is the radius.
- \(SA = 4\pi r^2,\) where \(SA\) is the surface area of a sphere and \(r\) is the radius.
- \(A = \pi a b, \) where \(A\) is the area of an ellipse and \(a\) and \(b\) are the semi-minor and semi-major axes.
 A circle is inscribed in a square. What is the ratio of the area of the circle to the area of the square?
A circle is inscribed in a square. What is the ratio of the area of the circle to the area of the square?
Approximating \( \pi\) using Polygons
By measuring the perimeter of these polygons, we can approximate the perimeter of the circle.

The perimeters of these \(n\)-gons can be obtained from regular polygons trigonometry and we can then use small-angle approximation to find the limit, \(2\pi.\)
An approximation for \(\pi\) can be derived from the perimeters of a circumscribed square and an inscribed square.

Let \(P_1\) be the perimeter of the larger square, \(P_2\) the perimeter of the smaller square, and \(C\) the circumference of the circle.
The circumference of the circle can then be approximated by the average of the two perimeters:
\[C\approx \frac{P_1+P_2}{2}.\]
If \(d\) is the diameter of the circle, then the length of a side of the larger square is also \(d\). The length of a side of the smaller square can be found using a special right triangle. This length is \(\frac{\sqrt{2}}{2}d\). Now we have
\[\begin{align} P_1&=4d\\ P_2&=2\sqrt{2}d. \end{align}\]
So, our approximation for the circumference is \(C\approx\big(2+\sqrt{2}\big)d\). Dividing this equation by \(d\) yields us an approximation for \(\pi:\)
\[\pi\approx 2+\sqrt{2}.\]
This isn't a particularly good approximation! However, better approximations can be obtained using a similar method with regular polygons with more sides.
Approximating \( \pi\) by Statistical Techniques
There are many simulations and statistical techniques that can be used to approximate \(\pi\). Long before computers were invented, the French mathematicians Buffon \((1707-1788)\) and Laplace \((1749-1827)\) proposed using a stochastic simulation to estimate the value of \(π\).
"Buffon's needle" famously approximates \(\pi\) using the fact that a straight needle is equally likely to land at any angle when it is tossed onto a plane.
Suppose \(n\) needles of length 1 are dropped onto a floor with strips of wood 1 unit apart. The expected value for the number of needles which cross two strips of wood is \(\frac{2}{\pi}\cdot n.\)

The crux of the proof is the idea of breaking up each needle into small segments. Loosely speaking, linearity of expectation tells us that the expected number of times that the needle will cross between two strips of wood is proportional to the length of the needle.
Thus, as a function of the length \(l,\) the expected number of crossings is \(cl\) for some constant \(c.\) However, consider a circle with diameter 1 (so circumference \(\pi\)); with probability 1, this circle will intersect exactly 2 of the wood-crossings. Hence, \(c\pi = 2,\) so \(c = \frac{2}{\pi}.\) If one is uncomfortable with the idea of a circle, consider approximating the circle by combining a bunch of very, very small linear segments. \(_\square\)
This results in an easy simulation technique for approximating \(\pi.\) Simply throw \(n\) needles on the floor, count the number of needles \(x\) which cross two strips of wood, and then \(\pi \approx \frac{2n}{x}.\) This type of simulation technique is known as a Monte Carlo simulation.
Another approximation is even simpler. Think about inscribing a circle in a square with sides of length \(2\), so that the radius \(r\) of the circle is of length \(1\).
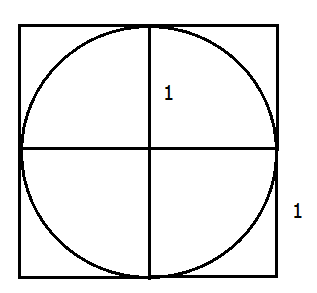
The true area of the circle is \(\pi r^{2}=\pi\). Buffon suggested that he could estimate the area of a circle by a dropping a large number of needles (which he argued would follow a random path as they fell) in the vicinity of the square. The ratio of the number of needles with tips lying within the square to the number of needles with tips lying within the circle could then be used to estimate the area of the circle:
\[\frac { { A }_{ c } }{ { A }_{ s } } =\frac { \pi { r }^{ 2 } }{ 4{ r }^{ 2 } } \implies \pi =4\frac { { A }_{ c } }{ { A }_{ s } }.\]

Applications of \( \pi\) in Complex Numbers, Trigonometry, and Euler's Formula
The number \(\pi\) is important in trigonometry, as it provides a more natural interpretation of angles than degrees do. Specifically, radians are defined so that \(2\pi\) radians are equivalent to a full circle (in other words, \(\pi\), understood as \(\pi\) radians, is commonly equal to 180 degrees when used in trigonometry); in this way, an angle of \(\theta\) corresponds to an arc length of \(\theta \cdot r\), where \(r\) is the radius of the circle. Equivalently, radians are defined so that one radian corresponds to an arc length equal to the radius of the circle.

This also allows for easy evaluation of trigonometric functions:
| \(\theta\) (in radians) | \(\sin\theta \hspace{10mm}\) | \(\cos\theta \hspace{10mm}\) | \(\tan\theta \hspace{10mm}\) |
| 0 | 0 | 1 | 0 |
| \(\frac{\pi}{6}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{3}}{3}\) |
| \(\frac{\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| \(\frac{\pi}{2}\) | 1 | 0 | undefined |
| \(\pi\) | 0 | -1 | 0 |
This also allows complex numbers to be presented in polar coordinates, meaning that any complex number can be written in the form \(re^{i\theta}\) for some real numbers \(r\) and \(\theta\). The number \(\pi\) plays a key role in their analysis, as this complex number is equivalent to
\[re^{i\theta}=r(\cos\theta + i\sin\theta)\]
as both sides represent the same point in the complex plane. Setting \(\theta = \pi\) gives the famous identity
\[e^{i\pi} + 1 = 0.\]
It is conjectured that this is the only nontrivial relation between the numbers \(e, i,\) and \(\pi\), making this result (known as Euler's formula) even more remarkable.
Exactly Defining \( \pi\) as an Infinite Series
Though \(\pi\) cannot be represented as any finite series of rational numbers (as a consequence of being irrational), there are many ways to express \(\pi\) as an infinite series. The "first," historically speaking, of these sequences was an infinite product:
\[\frac{2}{\pi} = \frac{\sqrt{2}}{2} \times \frac{\sqrt{2+\sqrt{2}}}{2} \times \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \times \cdots, \]
which, since the \(n^\text{th}\) term of the infinite product is \(\cos\frac{\pi}{2^n}\) by repeated application of the half-angle formula, is equivalent to the statement
\[\lim_{n \rightarrow \infty} \frac{1}{2^n\sin\frac{\pi}{2^{n+1}}} = \frac{2}{\pi},\]
which is true, as \(\sin\frac{\pi}{2^{n+1}}\approx \frac{\pi}{2^{n+1}}\) for large \(n\).
More useful series involves infinite sums rather than products, because calculating the first few terms of an infinite expression of \(\pi\) gives good approximations of its value. The simplest is the Gregory-Leibniz series, which uses the evaluation of the Taylor series of \(\arctan x\) at 1:
\[\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots.\]
However, this converges slowly, meaning that a large number of terms are necessary to get a good approximation of \(\pi\). Better series include Machin-like formulae:
\[\begin{align} \frac{\pi}{4} &= 4\arctan\frac{1}{5}-\arctan\frac{1}{239}\\ \frac{\pi}{4} &= 22\arctan\frac{24478}{873121}+17\arctan\frac{685601}{69049993}. \end{align}\]
In the modern computer era, even better series are known:
\[\frac{1}{\pi} = \frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{k!^4(396^{4k})},\]
which can be used to calculate millions of digits of \(\pi\).
Exactly Defining \(\pi\) as an Integral
\(\pi\) can also be defined in terms of integrals. The simplest are those that represent the area or perimeter of a circle:
\[\int_{-1}^1\sqrt{1-x^2}dx = \frac{\pi}{2},\]
as \(\left(x,\sqrt{1-x^2}\right)\) represents the top half of a circle over \([-1,1]\).
More complicated integrals come from statistics, such as the area under the normal distribution:
\[\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}\]
and the Cauchy distribution:
\[\int_{-\infty}^{\infty}\frac{1}{x^2+1}dx=\pi.\]
Finally, \(\pi\) appears in various expressions involving the gamma function, which is an extension of the factorial function defined as
\[\Gamma(t) = \int_0^{\infty}x^{t-1}e^{-x}dx,\]
which contains \(\pi\) when evaluated on half-integers. For example,
\[\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}, ~~\Gamma\left(\frac{5}{2}\right)=\frac{3}{4}\sqrt{\pi}.\]
More Digits
The first 500 digits of \( \pi\) are
\(\small 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 \\ \small 8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196 \\ \small 4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273 \\ \small 7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094 \\ \small 3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912...\)
For more digits, follow the link by clicking here.