Combinatorics
Combinatorics is the mathematics of counting and arranging. Of course, most people know how to count, but combinatorics applies mathematical operations to count quantities that are much too large to be counted the conventional way.
Combinatorics is especially useful in computer science. Combinatorics methods can be used to develop estimates about how many operations a computer algorithm will require. Combinatorics is also important for the study of discrete probability. Combinatorics methods can be used to count possible outcomes in a uniform probability experiment.
Contents
Rule of Product and Sum
Main Articles: Rule of Product and Rule of Sum
Combinatorics is often concerned with how things are arranged. In this context, an arrangement is a way objects could be grouped. The most basic rules regarding arrangements are the rule of product and the rule of sum. These rules govern how to count arrangements using the operations of multiplication and addition, respectively.
The rule of product governs how to count arrangements using multiplication.
Rule of Product
If there are \(m\) ways to arrange something, and then \(n\) ways to arrange something else after that, then the number of ways to arrange both of those things is \(m \times n.\)
The rule of sum governs how to count arrangements using addition. The language for these rules may seem similar. The main difference is that arrangements counted with the rule of product happen consecutively or simultaneously, while arrangements counted with the rule of sum cannot happen consecutively or simultaneously.
Rule of Sum
If there are \(m\) ways to arrange something, and there are \(n\) ways to arrange something else, and these arrangements cannot both happen, then the number of ways to arrange either of those things is \(m + n.\)
Many problems in combinatorics can be solved by applying these simple rules. In fact, the more advanced formulas in combinatorics are just extensions of these rules. One potential pitfall in counting problems is the concept of double counting. Double counting is an error in which the same object or arrangement is counted more than once.
How many integers between 1 and 100 are divisible by 7 or 13?
The number of integers between 1 and 100 that are divisible by 7 is \(\left\lfloor \frac{100}{7} \right\rfloor=14.\)
The number of integers between 1 and 100 that are divisible by 13 is \(\left\lfloor \frac{100}{13} \right\rfloor=7.\)It might seem like the rule of sum would be applicable here, and that the answer would be \(7+14=21.\) However, this would be an error in double counting. One must consider that it's possible for an integer to be divisible both by 7 and 13.
The number of integers between 1 and 100 that are divisible by 7 and 13 is \(\left\lfloor \frac{100}{7\times 13} \right\rfloor=1.\)
To account for the double counting, this amount is subtracted from the original answer of 21. Thus, there are \(20\) integers between 1 and 100 that are divisible by 7 or 13. \(_\square\)
The process of "removing" elements that are double counted is formalized with the principle of inclusion and exclusion.
Permutations and Combinations
Main Articles: Permutations and Combinations
See Also: Binomial Coefficient
A permutation is an arrangement of objects with regard to order. In combinatorics, the focus is usually on counting the number of elements in a set of permutations.
How many permutations are there of the letters \(\text{ABC}?\)
The permutations are
\[\begin{array}{lll} \text{ABC} & \text{ACB} & \text{BAC} \\ \text{BCA} & \text{CAB} & \text{CBA.} \end{array}\]
There are \(\boxed{6}\) permutations. \(_\square\)
Given a set of \(n\) distinct objects, let the set of permutations of those objects be \(P.\) Then,
\[|P|=n!,\]
where \(!\) is the factorial operator.
There are \(n\) ways to choose the first object in the order. Then, there are \(n-1\) ways to choose the second object in the order. This continues until there is only \(1\) way to select the last object in the order. By the rule of product, the number of permutations of \(n\) objects is
\[n \times (n-1) \times (n-2) \times \cdots \times 2 \times 1=n!.\ _\square\]
Permutations of a subset of objects can also be considered.
How many permutations are there of 2 letters from \(\text{ABCD}?\)
The permutations are
\[\begin{array}{lll} \text{AB} & \text{AD} & \text{BD} \\ \text{BA} & \text{DA} & \text{DB} \\ \text{AC} & \text{BC} & \text{CD} \\ \text{CA} & \text{CB} & \text{DC.} \end{array}\]
There are \(\boxed{12}\) permutations. \(_\square\)
Given a set of \(n\) objects, let the set of permutations of \(k\) of those objects be \(S.\) Then,
\[|S|=\frac{n!}{(n-k)!}.\]
A combination is an arrangement of objects without regard to order.
Given a set of \(n\) distinct objects, let \(C\) be the set of combinations of \(k\) of those objects. Then,
\[|C|=\binom{n}{k}=\frac{n!}{k!(n-k)!},\]
where \(\binom{\cdot}{\cdot}\) is the binomial coefficient operator.
The number of permutations of \(k\) objects from a set of \(n\) objects is \(\frac{n!}{(n-k)!}.\) For each subset of \(k\) objects from the set of \(n\) objects, there are \(k!\) permutations of that subset. Therefore, the number of combinations of \(k\) objects from a set of \(n\) objects is
\[\frac{n!}{(n-k)!} \div k!=\frac{n!}{k!(n-k)!}=\binom{n}{k}.\ _\square\]
The binomial coefficient operator received its name because of its application to the binomial theorem below. However, this operator has a wide use for computing numbers of combinations.
Combinations can be used to count outcomes in a probability experiment. This is especially useful when the probability experiment is uniform. In this case, the probability is just a ratio of numbers of combinations.
Binomial Theorem
Main Article: Binomial Theorem
The binomial theorem gives the polynomial expansion of a binomial raised to a positive integer power.
\[\begin{align} (a+b)^n &= \sum\limits_{k=0}^{n}\binom{n}{k}a^{n-k}b^k \\ \\ &= \binom{n}{0}a^n+\binom{n}{1}a^{n-1}b+ \cdots +\binom{n}{n-1}ab^{n-1}+\binom{n}{n}b^n \end{align}\]
One can establish a bijection between the products of a binomial raised to \(n\) and the combinations of \(n\) objects. Each product which results in \(a^{n-k}b^k\) corresponds to a combination of \(k\) objects out of \(n\) objects. Thus, each \(a^{n-k}b^k\) term in the polynomial expansion is derived from the sum of \(\binom{n}{k}\) products. \(_\square\)
These are the expansions of \( (x+y)^n \) for small values of \( n: \)
\[ \begin{eqnarray} (x+y)^0 &=& 1 \\ (x+y)^1 &=& x+y \\ (x+y)^2 &=& x^2 + 2xy + y^2 \\ (x+y)^3 &=& x^3 + 3x^2y + 3xy^2 + y^3 \\ (x+y)^4 &=& x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4 \\ &\vdots& \end{eqnarray} \]
When we look at the coefficients in the expressions above, we find the following pattern:
\[1\\ 1\quad 1\\ 1\quad 2 \quad 1\\ 1\quad 3 \quad 3 \quad 1\\ 1\quad 4 \quad 6 \quad 4 \quad 1\\ 1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1\\ \cdots\]
This is called the Pascal's triangle.
Although the formula above is only applicable for binomials raised to an integer power, a similar strategy can be applied to find the coefficients of any linear polynomial raised to an integer power.
Principle of Inclusion and Exclusion
Main Article: Principle of Inclusion and Exclusion
The principle of inclusion and exclusion describes how to compute the number of elements in intersections and unions of sets.
How many integers between 1 and 1000 (inclusive) are divisible by 3, 5, or 7?
The number of integers divisible by 3 is \( \left\lfloor \frac{1000}{3} \right\rfloor = 333.\)
The number of integers divisible by 5 is \( \left\lfloor \frac{1000}{5} \right\rfloor = 200.\)
The number of integers divisible by 7 is \( \left\lfloor \frac{1000}{7} \right\rfloor = 142.\)Integers that are divisible by 3 and 5 are divisible by 15. The number of integers divisible by 15 is \( \left\lfloor \frac{1000}{15} \right\rfloor = 66.\)
Integers that are divisible by 3 and 7 are divisible by 21. The number of integers divisible by 21 is \( \left\lfloor \frac{1000}{21} \right\rfloor = 47.\)
Integers that are divisible by 5 and 7 are divisible by 35. The number of integers divisible by 35 is \( \left\lfloor \frac{1000}{35} \right\rfloor = 28.\)Integers that are divisible by 3, 5, and 7 are divisible by 105. The number of integers divisible by 105 is \( \left\lfloor \frac{1000}{105} \right\rfloor = 9.\)
The principle of inclusion and exclusion gives the size of the set that is divisible by 3, 5, or 7:
\[333+200+142-66-47-28+9=543.\]
There are \(\boxed{543}\) integers between 1 and 1000 (inclusive) that are divisible by 3, 5, or 7. \(_\square\)
Coloring
Main Article: Coloring (Parity Arguments)
See Also: Hall's Marriage Theorem
Coloring is a strategy used to determine whether or not a tiling arrangement is possible. Rather than exhaustively searching for an arrangement that meets the requirement of a problem, it can sometimes be more efficient to test the color parity of all arrangements. Color parity is the concept that the coloring scheme for all possible arrangements must match the coloring scheme of the desired arrangement.
Can the figure below be tiled with \(1 \times 2\) dominoes?


If one attempted to find an arrangement that completely tiles the figure with dominoes, it would seem as though it is not possible. However, testing every possible arrangement would be difficult. Instead, consider a checkerboard coloring scheme.
A \(1 \times 2\) domino would have a similar coloring—1 black tile and 1 white tile. To tile the figure with dominoes, there would have to be an equal amount of black and white spaces. However, the figure at right contains 11 black tiles and 13 white tiles. Thus, a tiling is not possible. \(_\square\)
Graph Theory
Main Article: Graph Theory
Graph theory is the study of graphs, which are a collection of connected nodes.
 A basic graph of 3-cycle
A basic graph of 3-cycle
In combinatorics, one can study the traversals of a graph and the permutations of a graph.
Prove that it is impossible to traverse the following graph by travelling along each path exactly once. Any of the vertices may be selected as the starting vertex or ending vertex, and vertices may be passed more than once.

Suppose that it is possible to traverse the graph by travelling along each path exactly once. Consider how many times each vertex would be passed through. For every time a vertex is entered, it is also exited. Therefore, if each path is travelled exactly once, then each vertex should have an even number of paths coming from it. There is an exception if our graph has different starting vertex and ending vertex. These vertices should have an odd number of paths coming from them. There can only be one starting vertex and one ending vertex. However, the graph above has 4 vertices with an odd number of paths coming from them.
Thus, it is impossible to traverse the above graph by travelling along each path exactly once. \(_\square\)
The toy below is a rigid hexagon with a colored circle at each vertex. It is currently in its holder, which has corresponding colored circles at each vertex.
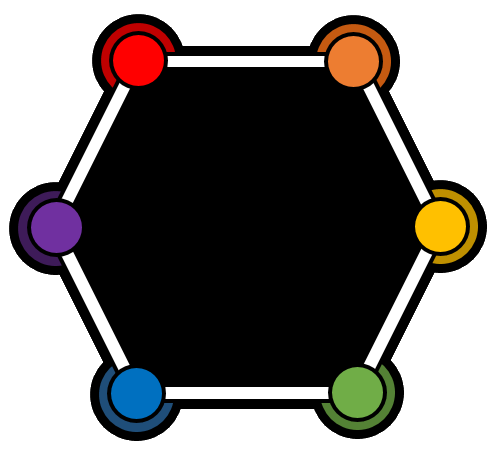
The toy is taken out of its holder, tossed around at random, and then placed back into the holder. What is the probability that the colors now match with the holder?
Note: The hexagon toy can be flipped upside down. The same colors are on the opposite side.
Recursion
Main Article: Recursion
See Also: Linear Recurrence Relations
Recursion formalizes the process of recognizing how solutions to smaller cases of a problem can, layer by layer, be built up to solve any case of a problem, no matter how enormous. Recursion is particularly important for developing formulas in combinatorics.
Give an expression for \(S_n \, (n=1, 2, 3, \ldots),\) which denotes the number of strings of \(n\) characters, consisting solely of \(\text{A}, \text{B},\) and/or \(\text{C},\) that contain no consecutive characters that are the same.
First consider strings of length 1:
\[\begin{array}{ccc} \text{A} & \text{B} & \text{C}. \end{array}\]
So, \(S_1=3.\) Now consider the strings of length 2:
\[\begin{array}{ll} \text{AB} & \text{AC} \\ \text{BA} & \text{BC} \\ \text{CA} & \text{CB.} \end{array}\]
So, \(S_2=6.\) Now consider the strings of length 3:
\[\begin{array}{llll} \text{ABC} & \text{ABA} & \text{ACA} & \text{ACB} \\ \text{BAB} & \text{BAC} & \text{BCA} & \text{BCB}\\ \text{CAB} & \text{CAC} & \text{CBA} & \text{CBC.} \end{array}\]
So, \(S_3=12.\) It is apparent that the number of strings doubles with each successive character. This is because there are 2 choices for the next character that is not the same as the last character. This can be expressed by the following:
\[S_n=3 \cdot 2^{n-1}.\ _\square\]
A string of \(n\) characters is made from the characters \(\text{A}\), \(\text{B}\), and \(\text{C}\).
Let \(G_n\) be the number of such strings of \(n\) characters which contain no instance of \(\text{AB}\) (in that order).
Write a recurrence relation for \(G_n\).
Distribution of Objects into Bins
Articles:
A distribution of objects into bins is a type of arrangement in which each object in a set is grouped into a bin.
Distributions of distinct objects have regard for which objects are grouped together in each bin. In contrast, distributions of identical objects have no regard for which objects are grouped together, only for how many objects are in each bin.
Distributions into distinct bins have regard for the order of the bins. In contrast, distributions into identical bins have no regard for the order of the bins, only for how the objects are grouped.
These distinctions create the four types of distributions into bins problems. As with other problems in combinatorics, the concern is usually in counting the number of possible distributions.
In an aquarium, there is a cichlid, tetra, goldfish, and danio. 14 food pellets are dropped into the aquarium. If all pellets are eaten, then how many possible distributions of pellets are there?
In this example, the "bins" are the fish, and the "objects" being distributed are the pellets. Each bin is distinct because it matters which fish gets the pellets. Each object is identical because it doesn't matter which pellets are consumed, only how many are consumed. Note that it is possible for a fish to receive 0 pellets. An effective way to solve an identical objects into distinct bins problem is to apply a stars and bars strategy.
\[{\color{red}\star \star} \mid {\color{blue}\star \star \star \star} \mid {\color{orange}\star \star \star \star} \mid {\color{green}\star \star \star \star} \]
The above arrangement represents a distribution of 2 pellets for the cichlid (in red), 4 pellets for the tetra (in blue), 4 pellets for the goldfish (in orange), and 4 pellets for the danio (in green). There are 14 stars and 3 bars in the representation, which gives 17 objects in total. One can obtain the representation for any distribution of the pellets by selecting 3 placements for the bars among the 17 possible placements. Thus, the number of distributions of pellets is
\[\binom{17}{3}=680.\ _\square\]
Partition of an Integer
Main Article: Partition of an Integer
A partition of an integer, sometimes referred to simply as a partition, is a sum of positive integers that equals a given integer. In combinatorics, the concern is in counting how many partitions of an integer exist.
How many partitions of 8 are there?
The partitions of 8 are as follows:
\[\begin{array}{cccc} 8 & 7+1 & 6+2 & 5+3 \\ 4+4 & 6+1+1 & 5+2+1 & 4+3+1 \\ 4+2+2 & 3+3+2 & 5+1+1+1 & 4+2+1+1 \\ 3+3+1+1 & 3+2+2+1 & 2+2+2+2 & 4+1+1+1+1 \\ 3+2+1+1+1 & 2+2+2+1+1 & \hspace{5mm} 3+1+1+1+1+1\hspace{5mm} &\hspace{5mm} 2+2+1+1+1+1\hspace{5mm} \\ \hspace{5mm} 2+1+1+1+1+1+1 \hspace{5mm} & \hspace{5mm} 1+1+1+1+1+1+1+1\hspace{5mm} \end{array}\]
There are \(\boxed{22}\) partitions of 8. \(_\square\)
Listing out all possible partitions can be a challenge. There is no known closed-form expression for the number of partitions of an integer \(n.\) Fortunately, there is a bijection between partitions and distributions of identical objects into identical bins. The same problem-solving approach can be taken.
Pigeonhole Principle
Main Article: Pigeonhole Principle
The pigeonhole principle describes how, given a certain number of bins and a greater number of objects placed into those bins, at least one bin must have more than one object.
5 points are placed within a unit equilateral triangle. Prove that two of those points must be a maximum distance of \(\frac{1}{2}\) from each other.

Suppose that for any pair of points among the 5, the distance between the points is greater than \(\frac{1}{2}\). Now consider the partition of the triangle into 4 smaller equilateral triangles.

Note that the maximum distance between two points within one of these smaller triangles is \(\frac{1}{2}.\) A point could be placed within each of the triangles (the 4 blue points) such that each point is further than \(\frac{1}{2}\) from the other points. However, the \(5^\text{th}\) point (the red one) would have to be placed within the same triangle as another point.

Thus, if 5 points are placed within a unit equilateral triangle, two of those points must be at most \(\frac{1}{2}\) away from each other. \(_\square\)
Grid Walking
Main Article: Rectangular Grid Walk
A grid walk is a path that is taken along a graph from a starting node to an ending node. In grid walk problem, the goal is to find the number of possible paths.
Moving only up or to the right, how many possible paths go from the starting node to the finish node?

Any path from the starting node to the finish node will require 3 up moves and 5 right moves. Consider the 8 moves to be a set of distinct objects. Then any combination of those moves in which 3 of them are up moves will be a valid path. Thus, the number of possible paths from the start node to the finish node is
\[\binom{8}{3}=56.\ _\square\]
