Discrete Mathematics

Discrete mathematics is the study of mathematical structures that are countable or otherwise distinct and separable. Examples of structures that are discrete are combinations, graphs, and logical statements. Discrete structures can be finite or infinite. Discrete mathematics is in contrast to continuous mathematics, which deals with structures which can range in value over the real numbers, or have some non-separable quality.

Since the time of Isaac Newton and until quite recently, almost the entire emphasis of applied mathematics has been on continuously varying processes, modeled by the mathematical continuum and using methods derived from the differential and integral calculus. In contrast, discrete mathematics concerns itself mainly with finite collections of discrete objects. With the growth of digital devices, especially computers, discrete mathematics has become more and more important.

Discrete structures can be counted, arranged, placed into sets, and put into ratios with one another. Although discrete mathematics is a wide and varied field, there are certain rules that carry over into many topics. The concept of independent events and the rules of product, sum, and PIE are shared among combinatorics, set theory, and probability. In addition, De Morgan's laws are applicable in many fields of discrete mathematics.

Often, what makes discrete mathematics problems interesting and challenging are the restrictions that are placed on them. Although the field of discrete mathematics has many elegant formulas to apply, it is rare that a practical problem will fit perfectly to a specific formula. Part of the joy of discovering discrete mathematics is to learn many different approaches to problem-solving, and then be able to creatively apply disparate strategies towards a solution.

Main Article: Combinatorics

Combinatorics is the mathematics of counting and arranging. Of course, most people know how to count, but combinatorics applies mathematical operations to count things that are much too large to be counted the conventional way.

Combinatorics is especially useful in computer science. Combinatorics methods can be used to develop estimates about how many operations a computer algorithm will require. Combinatorics is also important for the study of discrete probability. Combinatorics methods can be used to count possible outcomes in a uniform probability experiment.

Combinatorics is often concerned with how things are arranged. In this context, an arrangement is a way objects could be grouped. The most basic rules regarding arrangements are the rule of product and the rule of sum. These rules govern how to count arrangements using the operations of multiplication and addition, respectively.

A more specific type of arrangement is a permutation. A permutation is an arrangement of objects with regard to order.

A combination (not to be confused with combinatorics) is another type of arrangement that is related to permutations. A combination is an arrangement of objects without regard to order.

As a field of mathematics, combinatorics is nearly as broad as discrete mathematics. Other topics within combinatorics include

• derangements: a permutation such that no object is in its original spot in the order;

• rectangular grid walks: determining the number of ways a rectangular lattice can be traversed;

• distribution of objects into bins: determining how objects can be grouped into bins.

Main Article: Set Theory

See Also:

• Cardinality

• Union and Intersection

• Set Complement

• Principle of Inclusion and Exclusion

• De Morgan's Laws
  

Set theory is the branch of mathematics that is concerned about collections of objects. Sets can be discrete or continuous; discrete mathematics is primarily concerned with the former. At a basic level, set theory is concerned with how sets can be arranged, combined, and counted.

The cardinality of a finite set is the number of elements in that set. For a given set $A,$ its cardinality is denoted by $|A|.$

What is the cardinality of the set of prime numbers less than 25?

---

The set of prime numbers less than 25 is

$$\{2,3,5,7,11,13,17,19,23\}.$$

There are 9 elements in this set, so the cardinality is 9. $_\square$

Cardinality can also be extended to infinite sets. Although this kind of cardinality cannot be counted, each cardinality can be compared with another cardinality.

Let $A$ and $B$ be sets. Their cardinalities are compared as follows:

If there exists a bijection between $A$ and $B,$ then $|A|=|B|.$
If there exists an injective function from $A$ to $B,$ but no bijective function, then $|A|<|B|.$

Show that the set of integers and the set of even integers have the same cardinality.

---

It might seem strange that these sets have the same cardinality. After all, the even integers are more "rare." However, these sets are both infinite. Therefore, the "common sense" thinking about finite sets must be discarded. Instead, the goal is to obtain a bijective function from the set of integers to the set of even integers:

$$f(n)=2n, \ n \in \mathbb{Z}.$$

The function above gives a one-to-one correspondence between each integer $n$ and each even integer $2n.$ Since the bijection is established, the set of integers and the set of even integers have the same cardinality. $_\square$

A complement of a set $A$ is the set of elements that are not in $A.$ The study of set complements gives a number of efficient methods to calculate cardinalities of finite sets. For example, one can efficiently obtain the cardinality of a set that contains "at least one" element of another set.

The union and intersection give ways to describe how sets can be combined.

De Morgan's laws give identities for the complements of unions and intersections.

The principle of inclusion and exclusion, or PIE, gives a method to find the union or intersection of more than two sets.

Main Article: Graph Theory

Graph theory is the study of graphs, which are a collection of connected nodes.

A basic graph of 3-Cycle

Graphs are useful for representing all kinds of real-world problems.

Main Article: Probability

A probability is a number, between 0 and 1 inclusive, that represents the likelihood of an event. Discrete probability is a probability based on discrete sets of outcomes. The most basic type of probability is a uniform probability. If each outcome in a set is equally likely, then the probability of an event is equal to a ratio of cardinalities.

Let $S$ be a sample space of outcomes. If each outcome in this set is equally likely, then the probability of an event $A$ in $S$ is

$$P(A)=\frac{|A|}{|S|}.$$

Many of the rules of probability are analogous to the rules of combinatorics. The probabilistic rules of product, sum, and complement work similarly to those same rules from combinatorics. In addition, the structure of the probabilistic principle of inclusion and exclusion is the same as PIE for sets.

A discrete probability distribution is a function that takes a numerical outcome as an argument and gives a probability as a result. Discrete probability distributions can be created using the rules and guidelines described above. There are also some discrete probability distributions that show up in many problems:

• Geometric Distribution: Given repeated trials in which the probability of success is the same each time, this gives the probability that the first success will occur on a certain trial. Example: You roll a dice until you roll a 6. What is the probability that the first 6 will occur on the third roll?
• Binomial Distribution: Given a certain number of trials in which the probability of success is the same each time, this gives the probability of a certain number of successes. Example: You flip a coin 10 times. What is the probability that there will be exactly 5 heads?
• Poisson Distribution: Given a time period in which an event occurs a certain average number of times, this gives the probability that the event will occur a specific number of times. Example: A fast food drive-through gets 3 customers per minute. What's the probability they will get 4 customers in the next minute?

Although basic probabilities are based on discrete sets, the concept of probability can be extended to continuous sets by using concepts from calculus.

Main Article: Statistics

A statistic is a number used to describe a set of data or a probability distribution. Statistics is widely used in many fields outside of mathematics, from biology to politics to sports. The power of statistics lies in taking a massive, varied set of data and making sense out of it. Furthermore, statistics has the power to quantify confidence in those findings. Of course, the usefulness of statistics is not without controversy, but an understanding of its theoretical underpinnings can help one avoid its misuse.

One major kind of statistic is a measure of central tendency. A measure of central tendency is a number which describes what a value of a probability distribution or data set will tend to. An expected value is the theoretical long-run average outcome of a probability experiment when it is performed many times.

Somewhat related to the expected value is the mean. The mean is the average value of a set of numerical data.

Another major kind of statistic is a measure of variation. A measure of variation is a number which describes the distribution of a probability distribution or data set. The standard deviation of a probability distribution is a number that represents how much the outcomes differ from the expected value. Likewise, the standard deviation of a data set is a number that represents how much the elements of the set differ from the mean.

Although discrete statistics are based off of discrete events and probability distributions, these same concepts can be extended to continuous events and probability distributions using concepts from calculus.

Main Article: Bijection, Injection, and Surjection

A bijection is a relationship between two sets such that each element in a set is paired with exactly one element in the other set, and vice versa. Bijections can be applied to problem solving by establishing a bijection between a set that is difficult to enumerate and a discrete stucture that is well understood. By establishing a bijection, one can take advantage of the known formulas and theorems that the discrete structure affords.

The three Molloy siblings, April, Bradley, and Clark, have integer ages that sum to 15. How many possible distribution of ages are there?

Note: It is possible that an age can be 0, which means that the child was just born.

---

One can establish a bijection between the set of distributions of ages and a set of combinations. Consider the arrangement of stars and bars below:

$$\star \star \mid \star \star \star \star \mid \star \star \star \star \star \star \star \star \star$$

This arrangement corresponds to the following distribution of ages: April - 2, Bradley - 4, Clark - 9. Note that there are 15 stars and 2 bars in the arrangement above. This gives a total of 17 objects, 2 of which are bars. Placing the bars in different spots among the 17 placements will give a new distribution of ages. Thus, a bijection can be established between the set of distributions of ages and the set of combinations of 2 objects out of 17.

The number of distributions of ages is

$$\binom{17}{2}=136.\ _\square$$

Main Articles:

• Logical Puzzles

• Propositional Logic

• Boolean Algebra

A proposition is a statement that can either be true or false. Propositional logic aims to outline the rules of how these statements can be altered and combined.

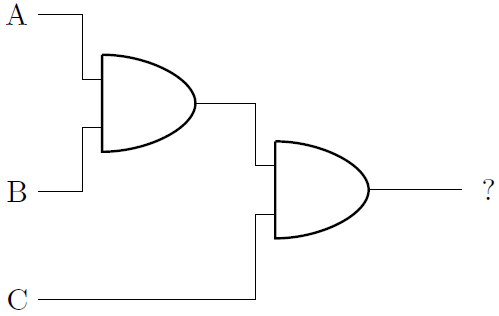
Similarly, Boolean algebra outlines the operations defined on variables that can take the values of true (1) or false (0). Boolean algebra is used to design computer circuits through logic gates, which take signal(s) as inputs and return a signal as an output.